01-Computation.html
13-AlgorithmsSoftware/find_max.py
“Simplicity is the key to brilliance.”
- Bruce Lee
document.querySelector('video').playbackRate = 1.2https://en.wikipedia.org/wiki/Algorithm
https://en.wikipedia.org/wiki/Time_complexity
https://en.wikipedia.org/wiki/Computational_complexity_theory
https://en.wikipedia.org/wiki/Computational_complexity
https://en.wikipedia.org/wiki/Asymptotic_analysis
How to measure the efficiency of an algorithm?
Empirical comparison (run example programs) - Pros and cons?
Asymptotic algorithm analysis (proofs) - Pros and cons?
Examples:
Searching through an array.
Sorting an array.
What impacts the efficiency of an algorithm?
For most algorithms, running time depends on “size” of the input.
Time cost is expressed as T(n), for some function T, on input size
n.
Draw this.
Discussion question:
Do all real-world problems have a parametrically varying size of
input?
Do all computatinal problems have a parametrically varying size of
input?
What is rate of growth?
How does T increase with n?
We refer back to a program from our first real class:
01-Computation.html
13-AlgorithmsSoftware/find_max.py
#!/usr/bin/python3
# -*- coding: utf-8 -*-
from typing import List
def find_max(L: List[int]) -> int:
max = 0
for x in L:
if x > max:
max = x
return max
print(find_max([11, 23, 58, 31, 56, 77, 43, 12, 65, 19]))Define a constant, c, the amount of time required to compare two
integers in the above function find_max, and thus:
T(n) = c * n
# python-style
sum = 0
for i in range(n):
for j in range(n):
sum = sum + 1
# c-style
sum = 0
for i = 1; i <= n; i = i + 1
for j = 1; j <= n; j = j + i
sum = sum + 1We can assume that incrementing takes constant time, call this time
c2, and thus:
T(n) = c2 * n2
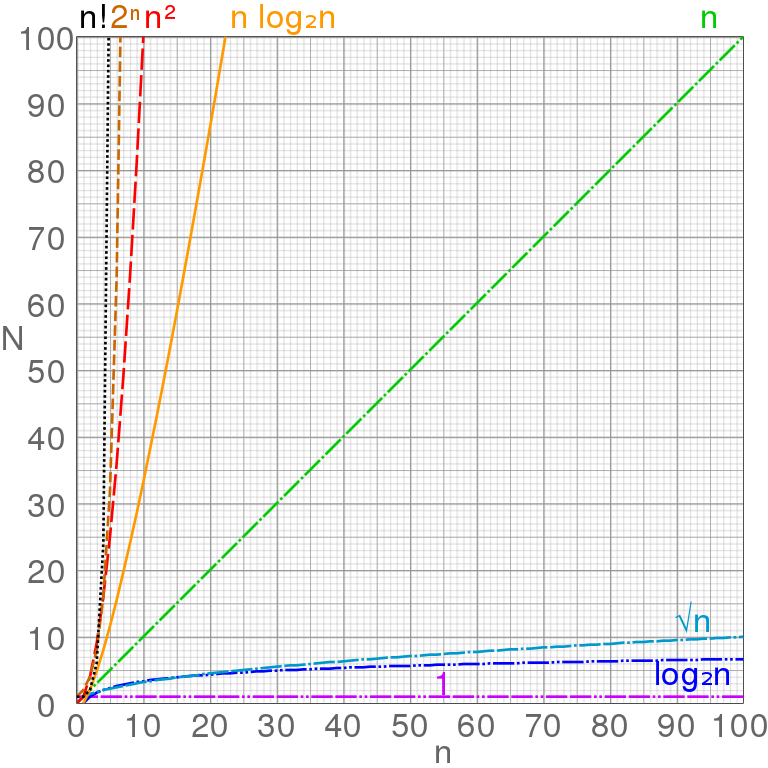
Rates of growth:
| Complexity class | Name |
|---|---|
| O(1) | constant |
| O(log log n) | double log |
| O(log n) | logarithmic |
| O(n) | linear |
| O(n log n) | quasi-linear |
| O(n^2) | quadratic |
| O(n^c) | polynomial |
| O(c^n) | exponential |
| O(n!) | factorial |
Rates of growth
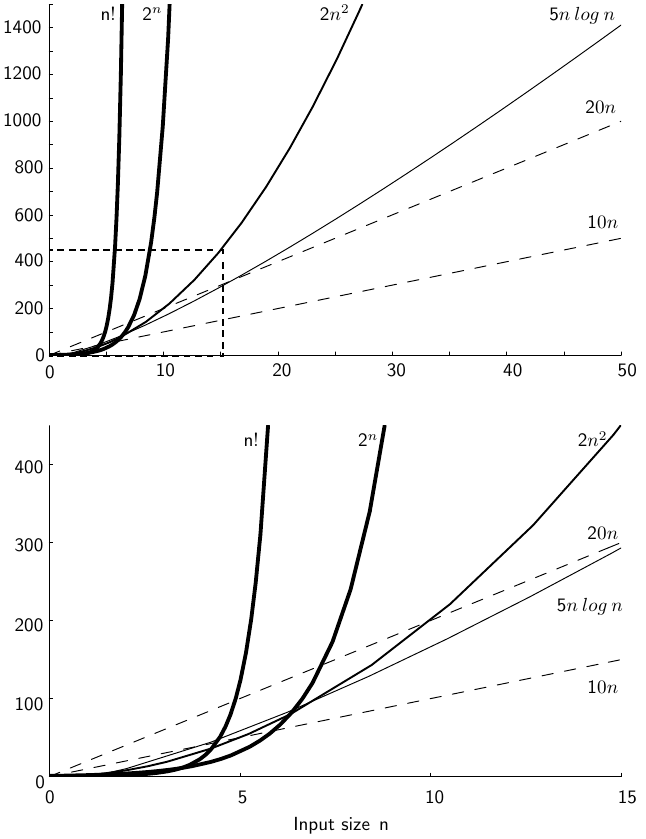
Discuss:
Small sizes don’t necessarily show the same ordinal value as large
sizes!
Good at large input does not necessarily mean good at small input.
This actually matters for some algorithms, or implementations, maybe a
server that processes lots of small batches
Mention: search versus sort trade-off for:
Your inbox,
Google’s search implementation
Rate of growth?
How does T increase with n?
https://en.wikipedia.org/wiki/Linear_search
13-AlgorithmsSoftware/alg_linear_search.py
#!/usr/bin/python3
# -*- coding: utf-8 -*-
from typing import List
def linear_search(numbers: List[int], key: int) -> int:
for i, number in enumerate(numbers):
if number == key:
return i
return -1
def main() -> None:
numbers: List[int] = []
numbers.append(2)
numbers.append(4)
numbers.append(7)
numbers.append(10)
numbers.append(11)
numbers.append(32)
numbers.append(45)
numbers.append(87)
print("NUMBERS: ")
print(numbers)
print("Enter a value: ")
key = int(input())
print("\n")
# This takes O(n)
keyIndex = linear_search(numbers, key)
if keyIndex == -1:
print(key)
print(" was not found")
else:
print("Found ")
print(key)
print(" at index ")
print(keyIndex)
if _name_ == "_main_":
main()Constant simple operations plus for() loop:
T(n) = c * n
Is this always true?
What if our array is randomly sorted?
What if our array is fully sorted?
What is our data distribution?
Not all inputs of a given size take the same time to run.
Example: search through an randomly permuted array for a value
Sequential search for K in an array of n integers:
Begin at first element in array and look at each element in turn until K
is found
Best case: ?
Worst case: ?
Average case: ?
While average time appears to be the fairest measure, it may be
difficult to determine or prove.
It requires knowledge of the input data distribution!
When is the worst case time important?
Which is best depends on the real world problem being solved!
“Any intelligent fool can make things bigger and more
complex.
It takes a touch of genius and a lot of courage to move in the opposite
direction.”
- https://en.wikipedia.org/wiki/E._F._Schumacher
Don’t worry if you don’t remember all the details of this.
We’ll cover it again, and again, and again…
https://en.wikipedia.org/wiki/Big_O_notation
Definition:
For T(n) a non-negatively valued function,
T(n) is in the set O(f(n)),
if there exist two positive constants c and n0,
such that T(n) <= c * f(n) for all n > n0:
Meaning:
For all data sets big enough (i.e., n > n0),
the algorithm always executes in less than c * f(n) steps,
in {best, average, worst} case.
For example, an algorithm may be in in O(n2) in the {best, average, worst} case.
Big-Oh (O) describes an upper bound.
Example: If T(n) = 3n2 then T(n) is in O(n2)
Look for the tightest upper bound:
While T(n) = 3n2 is in O(n3), we prefer
O(n2).
In image, everywhere to right of n0 (dashed vertical
line),
the lower line, f(n), is <= the top line, c * g(n),
thus f(n) is in O(g(n)):
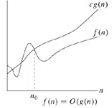
If visiting and examining one value in the array requires
cs steps, where cs is a positive number,
and if the value we search for has equal probability of appearing in any
position in the array,
then in the average case T(n) = cs * n / 2.
For all values of n > 1, cs * n/2 <= cs *
n.
Therefore, by the definition, T(n) is in O(n) for n0 = 1 and
c = cs
Big-Oh refers to a bounded growth rate as n grows to is infinity, in a general theoretical sense.
Best/worst case is defined for the input of size n
that happens to occur among all inputs of size,
when you get lucky or unlucky in a particular case.
Note: this definition uses set notation concepts:
https://en.wikipedia.org/wiki/Set-builder_notation
O(g(n)) = {
T(n) : there exist positive constants, c, n0, such
that:
0 <= T(n) <= c * g(n)
for all n >= n~0)
}
g(n) is an asymptotic upper bound for T(n)
Middle plot below is Big O
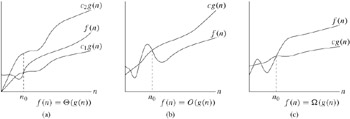
Any values of c?
Growth rate is the important factor (which is why we say that any c and
n0 work.)
https://en.wikipedia.org/wiki/Big_Omega_function
Omega(g(n)) = {
T(n) : there exist positive constants, c, n0, such
that:
0 <= c * g(n) <= T(n)
for all n >= n~0)
}
g(n) is an asymptotic lower bound for T(n)
Right plot below is Omega

Theta(g(n)) = {
T(n) : there exist positive constants
c1, c2, n0, such that
0 <= c1 * g(n) <= T(n) <= c2 * g(n)
for all n >= n_0
}
T(n) = Theta(g(n)) if and only if
T(n) is in O(g(n)) and
T(n) is in Omega(g(n))
g(n) is an asymptotically tight two-sided bound for T(n)
Left plot below is Theta

https://en.wikipedia.org/wiki/Big_O_notation#Little-o_notation
o(g(n)) = {
T(n) : for any positive constant c > 0,
there exists a constant n0 > 0 such that
0 <= T(n) < c * g(n)
for all n >= n~0)
}
g(n) is an upper bound for T(n) that may or may not be asymptotically tight.
omega(g(n)) = {
T(n) : for any positive constant c > 0,
there exists a constant n0 > 0 such that
0 <= c * g(n) < T(n)
for all n >= n~0)
}
g(n) is a lower bound for T(n) that is not asymptotically tight
++++++++++++++++++
Cahoot-13.1
“There can be economy only where there is
efficiency.”
- Benjamin Disraeli
if A < B and B < C,
then A < C
If T(n) is in O(f(n)) and f(n) is in O(g(n)),
then T(n) is in O(g(n))
If some function f(n) is an upper bound for your cost function,
then any upper bound for f(n) is also an upper bound for your cost
function.
Higher-order terms soon overpower the lower-order terms,
in their contribution to the total cost, as n becomes larger.
For example, if T(n) = 3n4 + 5n2, then T(n) is in
O(n4).
The n2 term contributes relatively little to the total cost
for large inputs.
Why?
If T(n) is in O(kf(n)) for any constant k < 0,
then T(n) is in O(f(n))
You can ignore any multiplicative constants in equations when using big-Oh notation.
Why??
If T1(n) is in O(f(n)) and T2(n) is in
O(g(n)),
then T1(n) + T2(n) is in O(f(n) + g(n)) which is
O(max(f(n), g(n)))
Given two parts of a program run in sequence (whether two statements
or two sections of code),
you need consider only the more expensive part.
Why??
If T1(n) is in O(f(n)) and T2(n) is in
O(g(n)),
then T1(n) * T2(n) is in O(f(n) * g(n))
If some action is repeated some number of times, and each repetition
has the same cost,
then the total cost is the cost of the action,
multiplied by the number of times that the action takes place.
If T(n) is a polynomial of degree k, then T(n) = Theta(nk)
logk N is in O(N) for any constant.
This tells us that logarithms grow very slowly.
“Simplicity is a great virtue,
but it requires hard work to achieve it,
and education to appreciate it.
And to make matters worse:
complexity sells better.”
- https://en.wikipedia.org/wiki/Edsger_W._Dijkstra
++++++++++++++++++
Cahoot-13.2
How do we determine the order or growth rate of our code?
The running time of a for loop is at most,
the running time of the statements inside the for loop (including
tests),
times the number of iterations.
Python style
~~~
sum = 0
for i in range(n):
sum = sum + n
~~~
C-style
~~~
sum = 0
for i = 1; i <= n; i = i + 1
sum = sum + n
~~~
The first line is constant, thus Theta(c1).
The for loop is repeated n times.
The third line takes constant time, thus Theta(c2).
T(n) = c1 + c2 * n
We eliminate canything.
Thus, he total cost for executing the two lines making up the for loop
is Theta(n).
Thus, the cost of the entire code fragment is also Theta(n).
Analyze these inside out.
Total running time of a statement inside a group of nested loops is the
running time of the statement,
multiplied by the product of the sizes of all the loops.
Python style
~~~
k = 0
for i in range(n):
for j in range(n):
k = k + 1;
~~~
C-style
~~~
k = 0
for i = 0; i < n; i = i + 1
for j = 0; j < n; j = j + 1
k = k + 1;
~~~
Inner statement is c.
Inner for loop is n.
That inner loop is done n times.
Thus, this one is Theta(n2).
Ask/Discuss: Are double nested for loops always n2 ?
These just add (recall the sum rule).
Python-style
~~~
for i in range(n):
a[i] = 0
for i in range(n):
for j in range(n):
a[i] = a[i] + a[j] + i + j
~~~
C-style
~~~
for i = 0; i < n; i = i + 1
a[i] = 0
for i = 0; i < n; i = i + 1
for j = 0; j < n; j = j + 1
a[i] = a[i] + a[j] + i + j
~~~
T(n) = n + n2
We discard the n, and it’s just Theta(n2).
Running time of an if/else statement is never more than the running
time of the test,
plus the larger of the running times of each branch.
Take greater complexity of then/else clauses.
Why?
Is this always valid?
What about data distribution?
“It’s not the most powerful animal that survives.
It’s the most efficient.”
- https://en.wikipedia.org/wiki/Georges_St-Pierre
a = bTheta(?)
Go line-by-line, from the inside out.
Python style
~~~
sum = 0
for i in range(n):
sum = sum + n
~~~
C-style
~~~
sum = 0
for i = 1; i <= n; i = i + 1
sum = sum + n
~~~
Theta(?)
Python-style
~~~
sum = 0
for i in range(n):
for j in range(i):
sum = sum + 1
for k in range(n):
A[k] = k
~~~
C-style
~~~
sum = 0
for i = 1; i <= n; i = i + 1
for j = 1; j <= i; j = j + 1
sum = sum + 1
for k=0; k<n; k = k + 1
A[k] = k
~~~
Outer for loop is executed n times, but each time the cost of the
inner loop is different with i increasing each time.
During the first execution of the outer loop, i = 1.
For the second execution of the outer loop, i = 2.
\(\sum_{i=1}^n i = n(n-1)/2\)
Theta(?)
https://en.wikipedia.org/wiki/Logarithm
CS is mostly \(\log_2 x\)
Why?
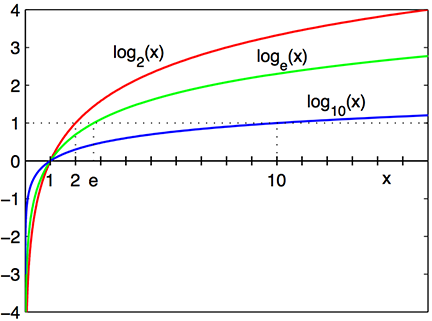
Logarithm is the inverse operation to exponentiation
\(\log_b x = y\)
\(b^y=x\)
\(b^{\log_b x}=x\)
Example:
\(\log_2 64 = 6\)
\(2^6=64\)
\(2^{\log_{2} 64}=64\)
\(\log_2 x\)
intersects x-axis at 1 and passes through the points with coordinates
(2, 1), (4, 2), and (8, 3), e.g.,
$_2 8 = 3 $
\(2^3=8\)
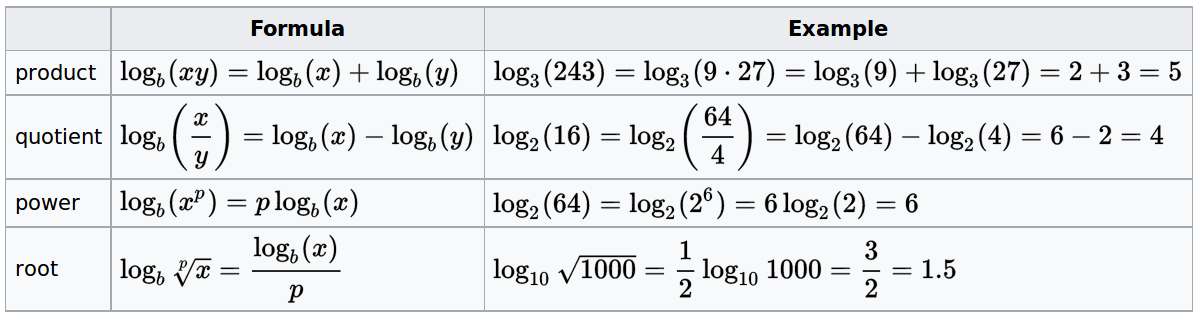
\(\log (nm) = \log n + \log m\)
\(\log (\frac{n}{m}) = \log n - \log m\)
\(\log(n^r) = r \log n\)
\(\log_a n = \frac{\log_b n}{\log_b
a}\)
(base switch)
Log general rule for algorithm analysis
Algorithm is in O(log2 n) if it takes constant, O(1), time to cut the problem size by a fraction (which is usually 1/2).
If constant time is required to merely reduce the problem by a
constant amount,
such as to make the problem smaller by 1,
then the algorithm is in O(n)
Caveat: Often, with input of n, an algorithm must
take at least Omega(n) to read inputs.
O(log2 n) classification often assumes input is pre-read…
++++++++++++++++++
Cahoot-13.3
++++++++++++++++++
Cahoot-13.4
"**Simplicity is the ultimate sophistication"**
- Source debated: Leonardo da Vinci? Clare Boothe Luce? Leonard Thiessen? Elizabeth Hillyer? William Gaddis? Eleanor All?https://en.wikipedia.org/wiki/Binary_search
13-AlgorithmsSoftware/alg_binary_search.py
#!/usr/bin/python3
# -*- coding: utf-8 -*-
from typing import List
def binary_search(numbers: List[int], key: int) -> int:
low: int = 0
high: int = len(numbers)
mid = (high + low) // 2
while high >= low and numbers[mid] != key:
mid = (high + low) // 2
if numbers[mid] < key:
low = mid + 1
elif numbers[mid] > key:
high = mid - 1
if numbers[mid] != key:
mid = -1
return mid
def main() -> None:
numbers: List[int] = []
numbers.append(2)
numbers.append(4)
numbers.append(7)
numbers.append(10)
numbers.append(11)
numbers.append(32)
numbers.append(45)
numbers.append(87)
print("NUMBERS: ")
print(numbers)
print("Enter a value: ")
key = int(input())
print("\n")
# This takes around O(n log n)
numbers.sort()
# This takes O(log n)
keyIndex = binary_search(numbers, key)
if keyIndex == -1:
print(key)
print(" was not found")
else:
print("Found ")
print(key)
print(" at index ")
print(keyIndex)
if _name_ == "_main_":
main()Binary search
Inside the loop takes Theta(c).
Loop starts with high - low = n - 1 and finishes with high - low <= -
1.
Each iteration, high - low must be at least halved from its previous
value.
Number of iterations is at most log2(n - 1) + 2.
For example, if high - low = 128,
then the maximum values of high - low after each iteration are:
64, 32, 16, 8, 4, 2, 1, 0, -1
This search is in Theta(log2 n)
An alternative way to think about this problem is recursively:
T(n) = T(n / 2) + 1
where for n > 1; T(1) = 1
which means this is T(n) = log2 n
https://en.wikipedia.org/wiki/Exponentiation
Compute bn in how many multiplications are involved?
13-AlgorithmsSoftware/alg_exp.py
#!/usr/bin/python3
# -*- coding: utf-8 -*-
print("Enter base, hit enter, then exponent")
base: int = int(input())
exponent: int = int(input())
total: int = 1
for counter in range(0, exponent):
total = total * base
print("Base ", base)
print(" to the power of ", exponent)
print(" is ", total)Theta(?)
Python-style
~~~
sum1 = 0
while k <= n: # Do log n times
k = k * 2
while j <= n: # Do n times
j = j + 1
sum1 = sum1 + 1
sum2 = 0
while k <= n: # Do log n times
k = k * 2
while j <= k: # Do k times
j = j + 1
sum2 = sum2 + 1
~~~
C-style
~~~
sum1 = 0
for k = 1; k <= n; k = k * 2 // Do log n times
for j = 1; j <= n; j = j + 1 // Do n times
sum1 = sum1 + 1
sum2 = 0
for k = 1; k <= n; k = k * 2 // Do log n times
for j = 1; j <= k; j = j + 1 // Do k times
sum2 = sum2 + 1
~~~
First outer for loop executed log n + 1 times
On each iteration k is multiplied by 2 until it reaches n.
Inner loop is always n.
Theta(n * log~2 ~n)
Second outer loop is log~2 ~n + 1
Second inner loop, k, doubles each iteration.
Theta(n)
https://en.wikipedia.org/wiki/Space_complexity
What are the space requirements for an array of of n integers?
Discuss: Mapping social networks for disease spread tracing. How do we
represent this?
To define binary connectivity between all elements with all other
elements, we can use a fully connected matrix:
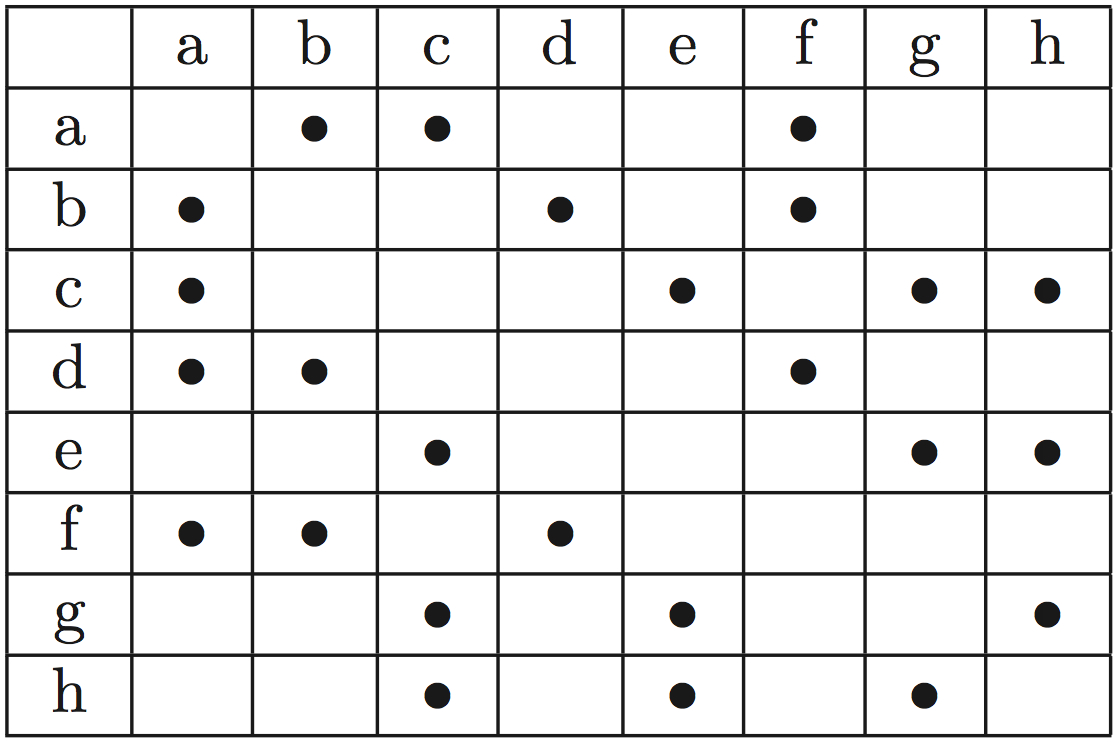
Dots imply connectivity.
What is Theta(?) here for space complexity?
Can we do better for this kind of binary connectivity?
Discuss: space-time tradeoff
Memoization, dynamic programming (simpler than we make it out to
be).
History of memory costs: memory is relatively cheaper compared to
processing power than it used to be.
“A designer knows he has achieved perfection not when there
is nothing left to add,
but when there is nothing left to take away.”
- Antoine de Saint-Exupery
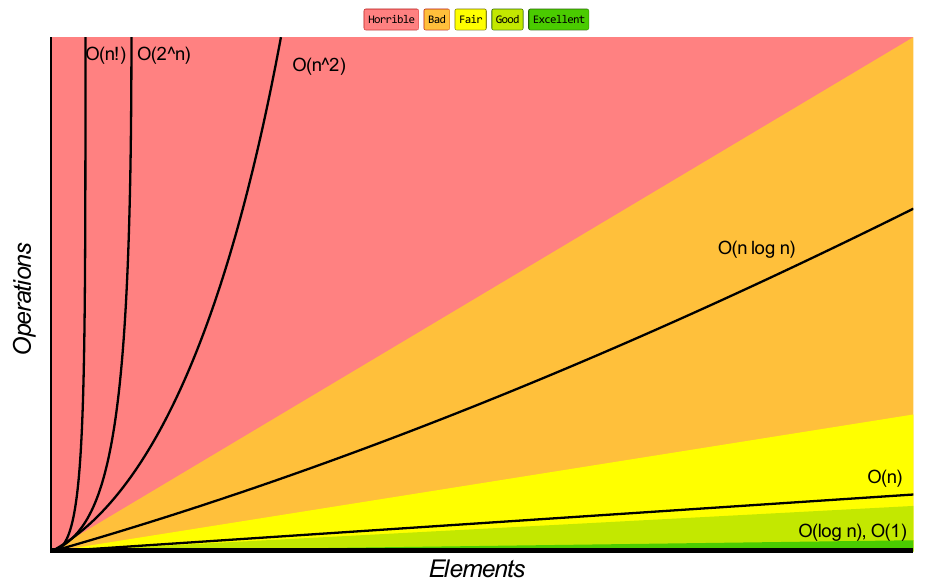
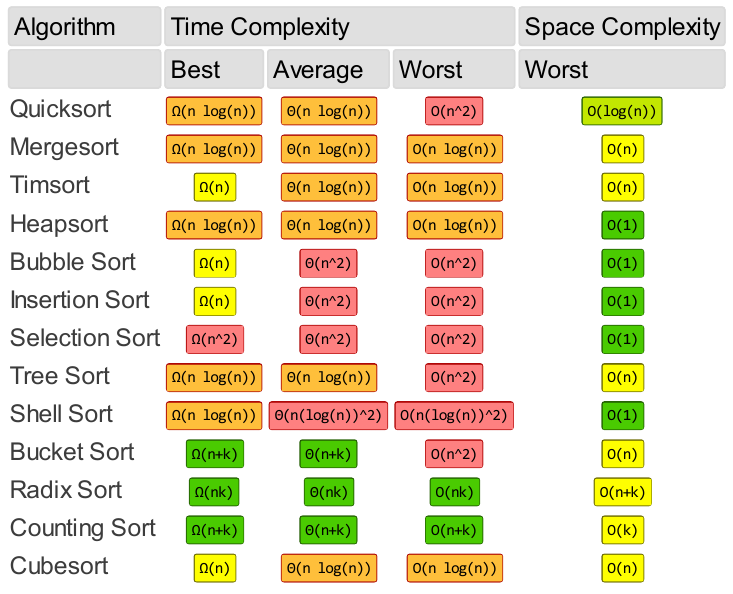
Array sorting algorithms for example:
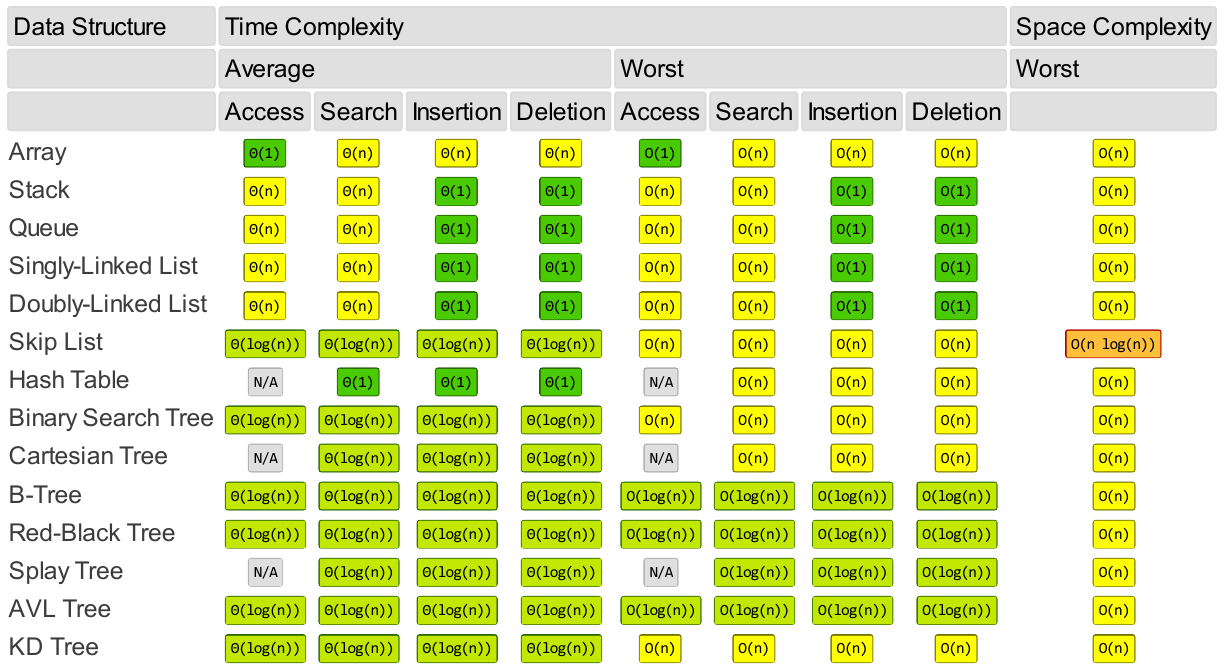
And data structures:
Would you rather have a faster algorithm or a faster computer?
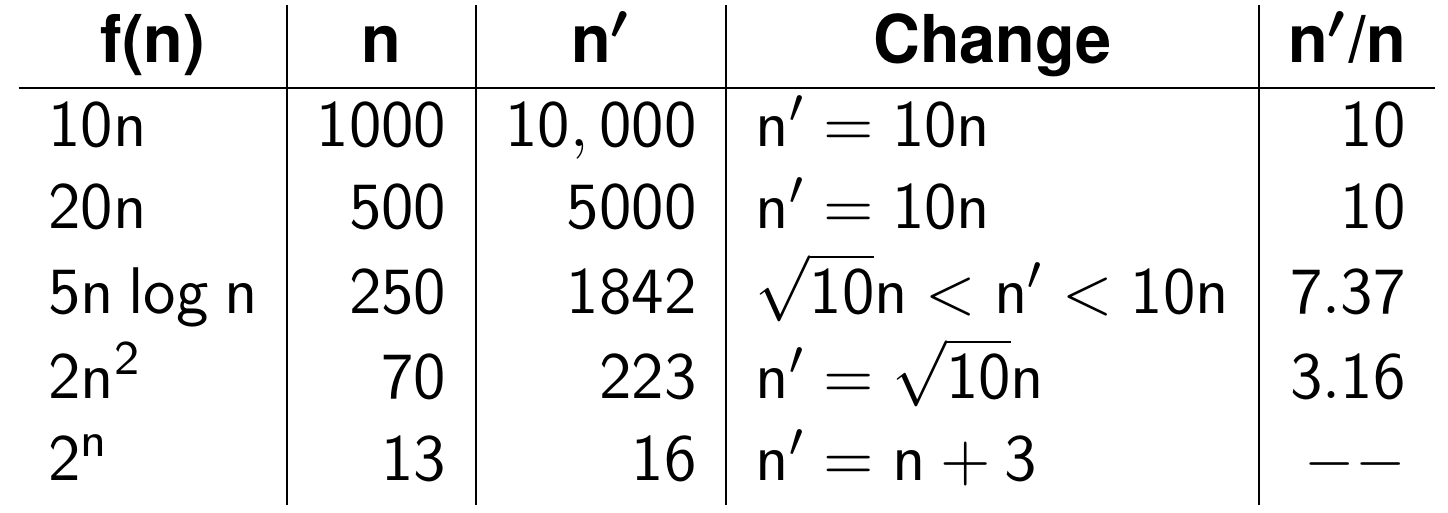
Growth rate | old computer | 10x faster computer | Delta | ratio
Analysis of algorithms applies to particular
solutions to problems,
which themselves have complexities defined by the
entire set of their solutions.
Problem: E.g., what is the least possible cost for any sorting algorithm in the worst case?
Any algorithm must at least look at every element in the input,
to determine that input is sorted,
which would be be c n with Omega(n) lower bound.
Further, we can prove that any sorting algorithm must have running time in Omega(n log n) in the worst case

Particularly in the case of academic publications…
Remember to:
https://en.wikipedia.org/wiki/KISS_principle