1 10b-IntegerSorts

1.1 All sorts of sorts

Hint: only some of these are jokes…

1.1.1 Bogo sort

https://en.wikipedia.org/wiki/Bogosort

while not is_sorted(array):
    shuffle(array)

1.1.2 Solar bit-flip sort

The alpha particles from the sun flip a few bits in the memory once a while,
so this algorithm basically hopes that this flipping can cause the elements to be sorted:
1. Check if the array is sorted.
2. If yes, praise your luck and print the magically sorted elements.
3. if no, wait for some random amount of time(Secretly hope that the alpha particles work their magic)
4. Go back to step 1.

1.1.3 Stupid sort

https://en.wikipedia.org/wiki/Gnome_sort

1.1.4 Quora sort

It’s works exactly like bubble sort, but for each comparison instead of using ‘<’ and ‘>’ operators it posts a question on Quora asking which value is greater.

For example, Quora question: Which is greater - 5 or 7?

1.1.5 Stooge sort

https://en.wikipedia.org/wiki/Stooge_sort

1.1.6 Dictator sort

1.1.7 Quantum bogo sort

1.2 Sorts for small integers with low variance

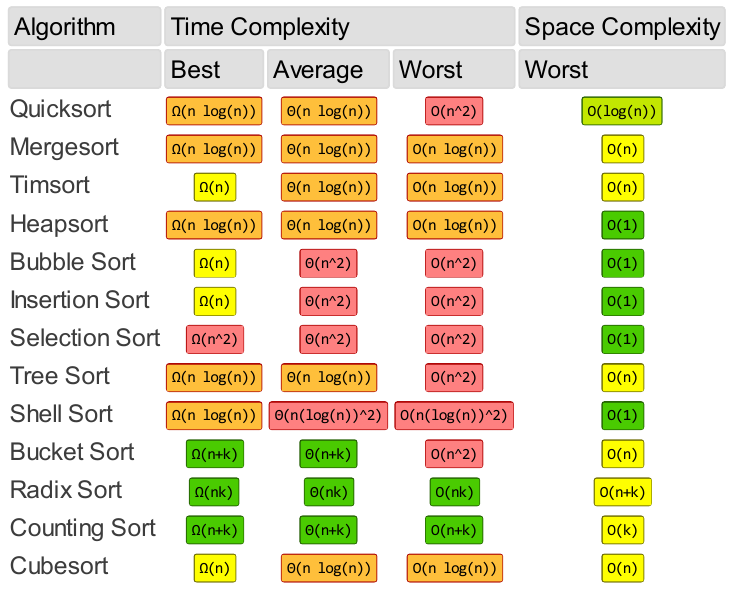
* Full comparison-based sorts can only do as fast as O(n(log(n)) in the average case.
* Bucket, Radix, and Counting sort are better for limited types of data

1.3 Bucket and bin sort

Ask: Given unlimited space, there is a perfect sorting algorithm, that can be coded in 2 lines. What is it?

1.3.1 The simplest and fastest sorting algorithm!!

for(i = 0; i < A.length; i++)
    B[A[i]] = A[i];

• Here the key value is used to determine the position for a record in the final sorted array.
• This is the most basic example of a Bin-sort, where key values are used to assign records to bins.
• Space-time trade-off makes this impractical for many purposes
• Ask:
  • What is the disadvantage of this awesome algorithm?
  • How do we ameliorate this disadvantage for arrays with a large variance in contained values?

1.3.2 Bucket sort

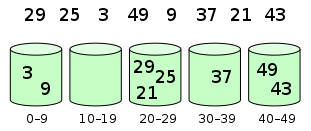
Elements are distributed into bins

Then, elements are sorted within each bin

• Bucket sort, or bin sort, is a sorting algorithm that works by distributing the elements of an array into a number of buckets.
• Each bucket is then sorted individually, either using a different sorting algorithm, or by recursively applying the bucket sorting algorithm.
• The 2nd in-bucket sorting algorithm could perhaps be insertion sort for small buckets, or quicksort for larger buckets
  

1.3.2.1 Algorithm

1. Set up an array of initially empty “buckets”.
2. Scatter: Go over the original array, putting each object in its bucket.
3. Sort each non-empty bucket.
4. Gather: Visit the buckets in order and put all elements back into the original array.

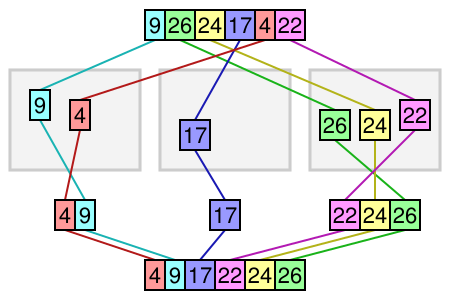
Using a list of lists

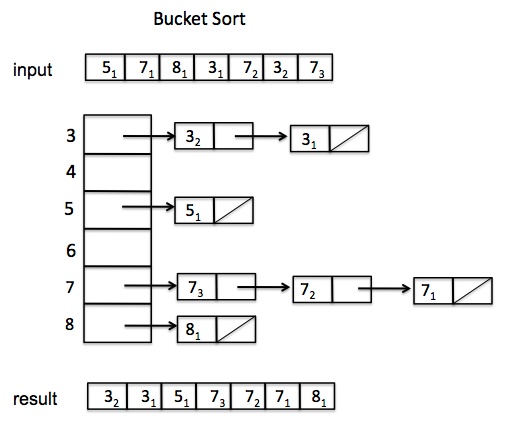
// Bucket sort
#include <iostream>
#include <algorithm>
#include <vector>

// Function to sort arr[] of size n using bucket sort
void bucketSort(float arr[], int n)
{
    // 1) Create n empty buckets
    std::vector<float> b[n];

    // 2) Put array elements in different buckets
    for(int i = 0; i < n; i++)
    {
        // Index in bucket - note, arr[i] is float,
        // so times ~10 will truncate the less significant end of the number.
        // Bucket indexing can vary widely.
        int bi = n * arr[i];
        b[bi].push_back(arr[i]);
    }

    // 3) Sort individual buckets
    for(int i = 0; i < n; i++)
        std::sort(b[i].begin(), b[i].end());

    // 4) Concatenate all buckets into arr[]
    int index = 0;
    for(int i = 0; i < n; i++)
        for (int j = 0; j < b[i].size(); j++)
            arr[index++] = b[i][j];
}

int main()
{
    float arr[] = {0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434};
    int n = sizeof(arr) / sizeof(arr[0]);

    bucketSort(arr, n);

    std::cout << "Sorted array is\n";

    for(int i = 0; i < n; i++)
        std::cout << arr[i] << " ";

    return 0;
}

1.4 Counting sort

* Counting sort is an algorithm for sorting a collection of objects according to keys that are small integers; that is, it is an integer sorting algorithm.
* The algorithm loops over the items, computing a histogram of the number of times each key occurs within the input collection.
* It then performs a prefix sum computation (a second loop, over the range of possible keys) to determine, for each key, the starting position in the output array of the items having that key.
* Finally, it loops over the items again, moving each item into its sorted position in the output array.

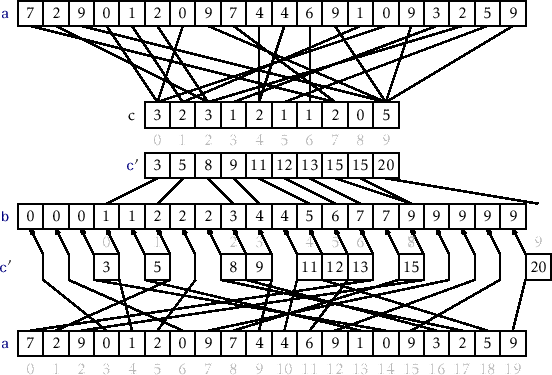
Ask: Is the algorithm faster with or without repeating numbers? If so, which, and why?

// Conting sort
#include <iostream>

// The main function that sorts the given string arr[] in
// alphabatical order
void countSort(char arr[], int n, int RANGE)
{
    // The output character array that will have sorted arr
    char output[n];

    // Create a count array to store count of inidividul
    // characters and initialize count array as 0
    // Note: this all-0s syntax only works with {0}
    int count[RANGE + 1]{0};
    int i;

    // Store count of each character
    // Ask: How is arr[i] interpreted here?
    for(i = 0; arr[i]; ++i)
        ++count[arr[i]];

    // Change count[i] so that count[i] now contains actual
    // position of this character in output array
    for(i = 1; i <= RANGE; ++i)
        count[i] += count[i - 1];

    // Build the output character array
    for(i = 0; arr[i]; ++i)
    {
        output[count[arr[i]] - 1] = arr[i];
        --count[arr[i]];
    }

    // Copy the output array to arr, so that arr now
    // contains sorted characters
    for(i = 0; arr[i]; ++i)
        arr[i] = output[i];
}

// Driver program to test above function
int main()
{
    const int RANGE =  255;
    char arr[] = "hello";
    int n = 5;

    countSort(arr, n, RANGE);

    std::cout << "Sorted character array is " << arr << "\n";

    return 0;
}

1.5 Radix sort

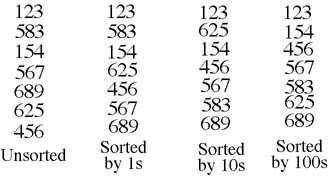
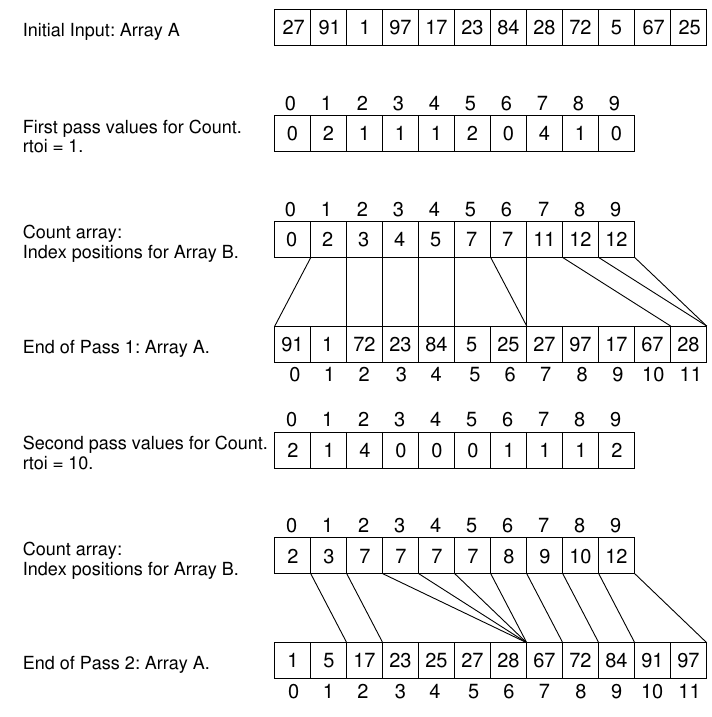
* Radix sort is a non-comparative integer sorting algorithm that sorts data with integer keys by grouping keys by the individual digits which share the same significant position and value.
* Ask: how is it non-comparative?
* A positional notation is required, but because integers can represent strings of characters (e.g., names or dates) and specially formatted floating point numbers, radix sort is not limited to integers (discussed at the end below).
* Ask: why low to high place?

1.5.1 Digits

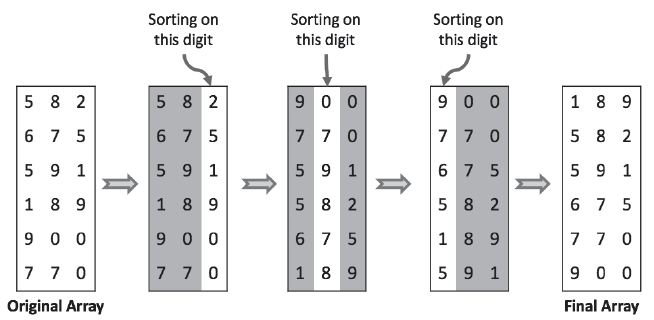
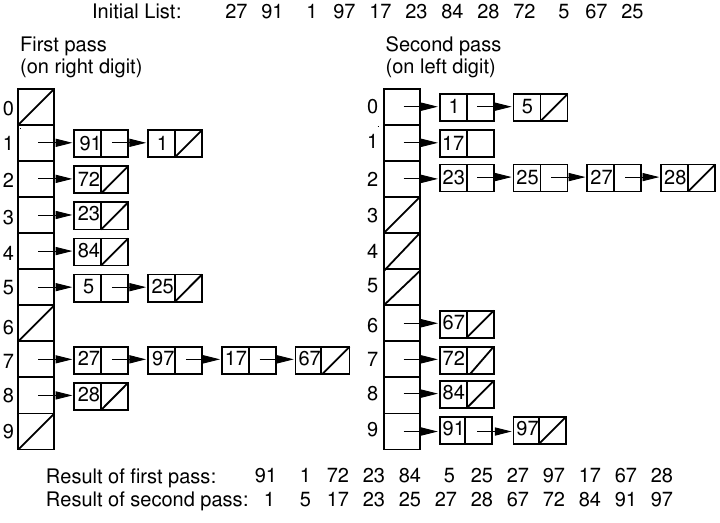
* Using a list of lists
* Note: All numbers do not need to be the exact same length, imagine leading 0s being sorted for higher places, even if they are not visualized

We can re-use a good sort for small integers (counting sort).
First, apply counting sort on 1’s, then 10’s, etc.

// Radix sort
#include <iostream>

// r, count array of size r (which is also the base, e.g., 2, 8, 10, 16)
// k, keys/digits (number of digits in the largest number to sort)
// n, size (number of elements in the array to sort)
// This algorithm requires k passes over the list of n numbers in base r
void radixsort(int A[], int k, int r, int n)
{
    int B[n];

    // This guarantees init to 0 for whole array, right?
    int count_arr[r]{0};

    int i, j, rtok;

    // Loop over place (0s, 10s, 100s, etc.)
    // Do a count sort within
    for(i = 0, rtok = 1;
        i < k;
        i++, rtok *= r)
    {
        // Count the number of records in each bin on this pass
        for(j = 0; j < n; j++)
            count_arr[(A[j] / rtok) % r]++;

        // count[j] will be index in B
        // First, reduce count[0] because indexing starts at 0, not 1
        count_arr[0] = count_arr[0] - 1;

        // Prefix sum on count array
        for(j = 1; j < r; j++)
            count_arr[j] += count_arr[j - 1];

        // Put records into location, working from bottom
        // Since fill from bottom, j counts downwards
        for(j = n - 1; j >= 0; j--)
        {
            B[count_arr[(A[j] / rtok) % r]] = A[j];

            --count_arr[(A[j] / rtok) % r];
        }

        for (j = 0; j < n; j++)
            A[j] = B[j];  // Copy B back
    }
}

int main()
{
    int arr[] = {3, 2, 9, 4, 7};
    int n = 5;
    int r = 10;
    int k = 1;

    radixsort(arr, k, r, n);

    for(int c = 0; c < n; c++)
        std::cout << arr[c] << "\n";

    return 0;
}

1.5.2 Binary

Radix sort is not limited to base 10.

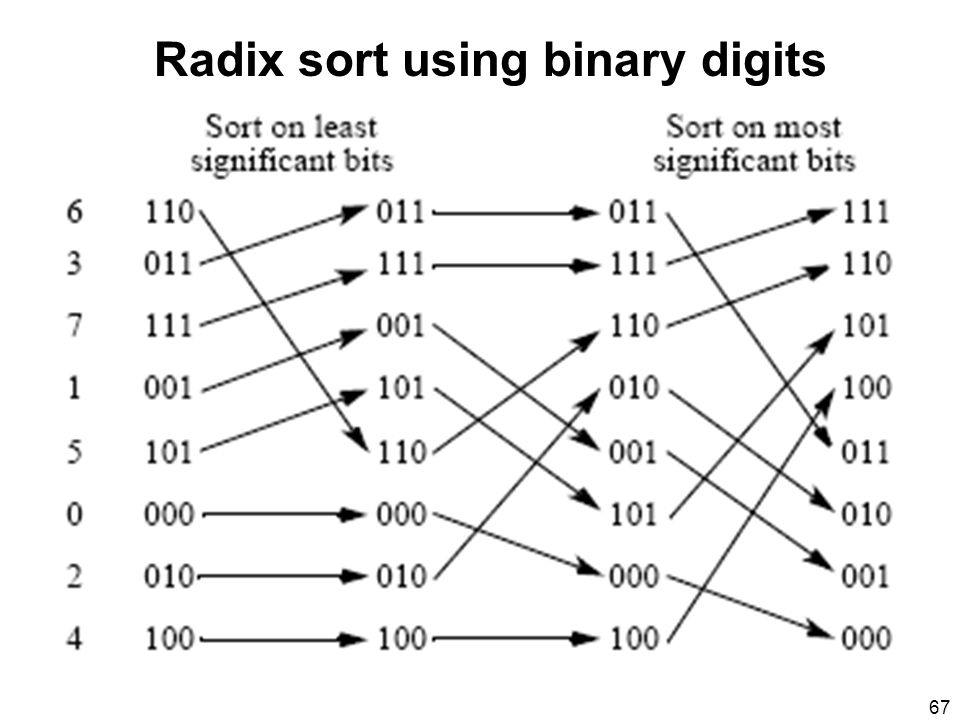
Ask:
* Is it more efficient to sort the same numbers in base 10 or base 2?
* Which loops/steps have more iterations?
* Which loops/steps have fewer iterations?

1.5.3 Strings

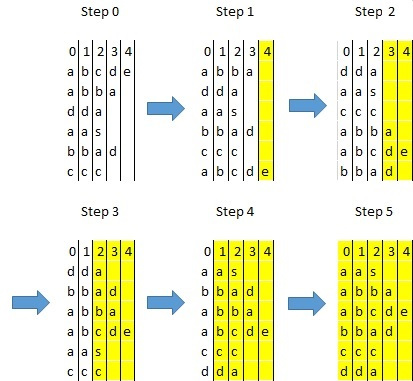
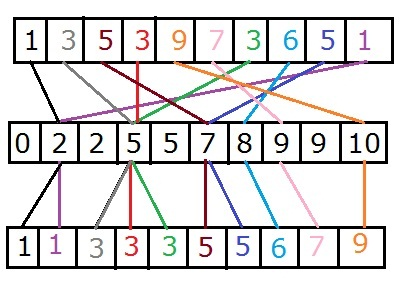
General notes:
* Some of these sorts are not only for integers, for example, when converting to an integer preserves the original order (ASCII).
* These sorts would not be useful if the encoding scheme did not preserve order.
* Whether data should be “aligned” left or right depends on the goal of the sort.
* For example see above, where:
* characters are aligned left (trailing 0s),
* as opposed to the integers, which were aligned right (leading 0s).