Discrete Mathematics using a Comptuter (O’Donnell, Hall, Page) Chapter 10
Discrete Mathematics with Applications - Metric Edition (Epp) Chapter 8
The Haskell Road to Logic, Math and Programming (Doets, van Eijck) 5
https://www.cs.carleton.edu/faculty/dln/book/ch08_relations_2021_September_08.pdf
https://www.cs.yale.edu/homes/aspnes/classes/202/notes.pdf Chapter 9
https://runestone.academy/ns/books/published/ads/chapter_6.html
https://runestone.academy/ns/books/published/ads/s-basic-definitions.html
https://runestone.academy/ns/books/published/ads/s-graphs-of-relations-on-a-set.html
https://runestone.academy/ns/books/published/ads/s-properties-of-relations.html
https://runestone.academy/ns/books/published/ads/s-matrices-of-relations.html
https://runestone.academy/ns/books/published/ads/s-closure-operations-on-relations.html
https://runestone.academy/ns/books/published/DiscreteMathText/chapter8.html
https://runestone.academy/ns/books/published/DiscreteMathText/relations8-1.html
https://runestone.academy/ns/books/published/DiscreteMathText/rstrelations8-2.html
https://runestone.academy/ns/books/published/DiscreteMathText/equivalencerelations8-3.html
https://runestone.academy/ns/books/published/DiscreteMathText/modarith8-4.html
https://en.wikipedia.org/wiki/Relation_(mathematics)
https://en.wikipedia.org/wiki/Codomain
https://en.wikipedia.org/wiki/Range_of_a_function
https://en.wikipedia.org/wiki/Image_(mathematics)


A relation denotes some kind of relationship between two objects in a
set, which may or may not hold.
Formally, a relation R over a set X can be seen as a set of ordered
pairs (x,y) of members of X.
The relation R holds between x and y if (x,y) is a member of R.
A binary relation R, with type R :: A × B, is a subset of A ×
B,
where A is the domain, and B is the codomain of R.
For x ∈ A and y ∈ B, the notation x R y means (x, y) ∈ R.
A relation is a set of ordered pairs.
Where R is a relation, instead of (x, y) ∈ R,
one usually writes xRy, or R(x, y), or Rxy.
The set dom(R) = {x | ∃y ( xRy )},
i.e., the set consisting of all first coordinates of pairs in R,
is called the domain of R and ran(R) = {y | ∃x ( xRy )},
the set of second coordinates of pairs in R, its range.
The relation R is a relation from A to B or between A and B,
if dom(R) ⊆ A and ran(R) ⊆ B.
A relation from A to A is called on A.
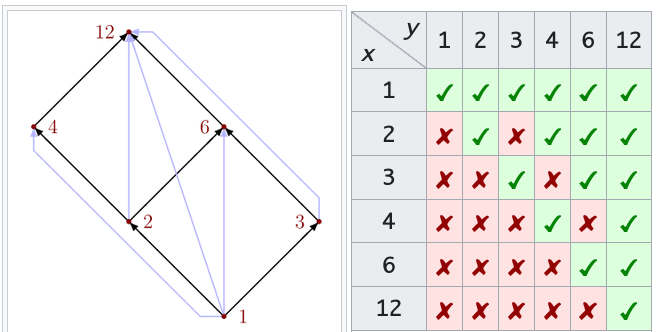
Directed graph (digraph):
Each member of X corresponds to a vertex;
if and only if (x,y) ∈ R,
then a directed edge from x to y exists,
Let A be a set, and let R be a binary relation R :: A × A.
The digraph D of R is the ordered pair D = (A, R).
A directed path is a set of arcs that can be arranged in a
sequence,
so that the end point of one arc in the sequence is the start point of
the next.
Boolean matrix:
The members of X are arranged in some fixed sequence x1, …, xn;
the matrix has dimensions n × n,
with the element in line i, column j, ✓, if (xi,xj) ∈ R, and X,
otherwise.


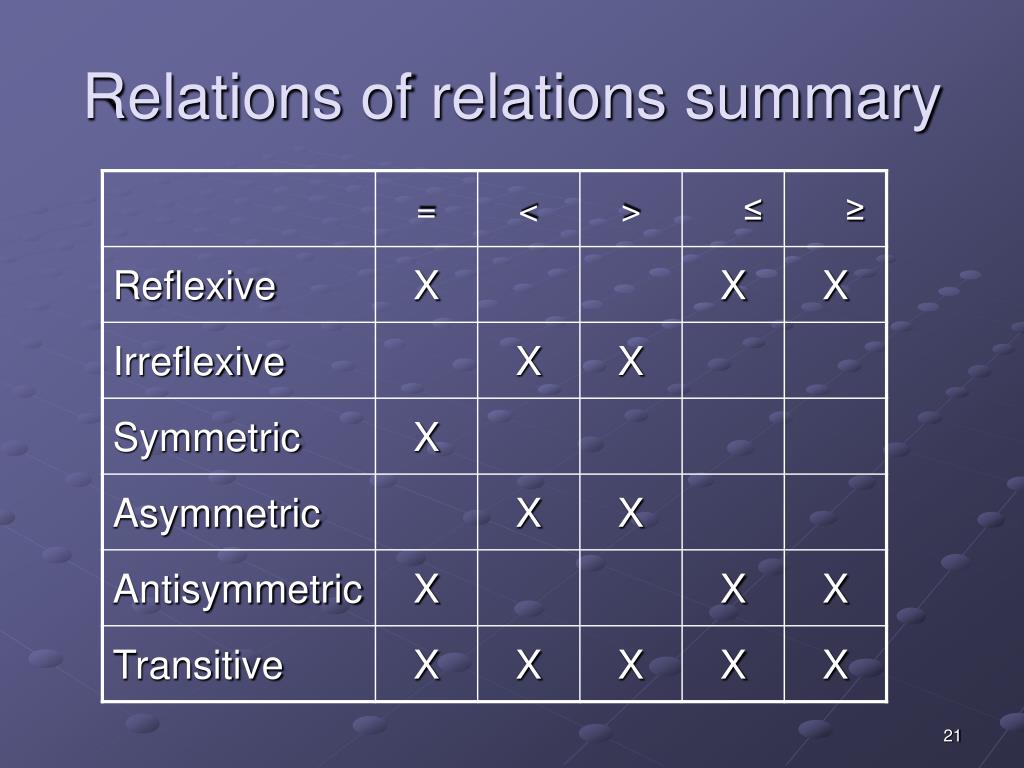
Reflexive
∀x xRx.
for all x ∈ X, xRx.
For example, ≥ is a reflexive relation but > is not.
In a reflexive relation, every element of the domain is related to
itself.
A binary relation R over A is reflexive if xRx for every element x of the
domain A.
Irreflexive (or strict)
∀x ¬xRx.
for all x ∈ X, not xRx.
For example, > is an irreflexive relation, but ≥ is not.
A relation is irreflexive if no element of its domain is related to
itself.
A binary relation R over A is irreflexive if,
for every x ∈ A, it is not the case, that xRx.
Symmetric
∀xy (xRy ⇒ yRx).
for all x, y ∈ X, if xRy then yRx.
For example, “is a blood relative of” is a symmetric relation,
if and only if, y is a blood relative of x,
then x is a blood relative of y.
Some relations have the property that:
the order of two related objects does not matter;
that is, if xRy it must also be true that yRx.
Such a relation is called a symmetric relation.
Let R :: A × A be a binary relation.
Then R is symmetric if ∀x, y ∈ A. xRy → yRx.
Asymmetric
∀xy (xRy ⇒ ¬yRx).
for all x, y ∈ X, if xRy then not yRx.
A relation is asymmetric, if and only if, it is both antisymmetric and
irreflexive.
For example, > is an asymmetric relation, but ≥ is not.
Antisymmetric
∀xy (xRy ∧ yRx ⇒ x = y).
for all x, y ∈ X, if xRy and yRx then x = y.
For example, ≥ is an antisymmetric relation;
so is >, but vacuously (the condition in the definition is always
false).
An antisymmetric relation is one where:
for all distinct values a and b,
it is never the case that both aRb and bRa.
A binary relation R :: A × A is antisymmetric if:
∀x, y ∈ A. xRy ∧ yRx → x = y.
Transitive
∀xyz (xRy ∧ yRz ⇒ xRz).
for all x, y, z ∈ X, if xRy and yRz then xRz.
A transitive relation is irreflexive, if and only if, it is
asymmetric.
For example, “is ancestor of” is a transitive relation, while “is parent
of” is not.
If x, y, and z are three people,
and you know that x is a sister of y,
and y is a sister of z,
then x must also be a sister of z.
Similarly, if you know that x < y, and also that y < z,
then it must also be the case that x < z.
Relations that have this property are called transitive relations.
A binary relation R :: A × B is transitive if:
∀x, y, z ∈ A. xRy ∧ yRz → xRz.
Intransitive
∀xyz (xRy ∧ yRz ⇒ ¬xRz).
Linear
∀xy (xRy ∨ yRx ∨ x = y).
Connected
for all x, y ∈ X, if x ≠ y then xRy or yRx.
For example, on the natural numbers, < is connected,
while “is a divisor of” is not (e.g. neither 5R7 nor 7R5).
Strongly connected
for all x, y ∈ X, xRy or yRx.
For example, on the natural numbers, ≤ is strongly connected, but <
is not.
A relation is strongly connected if, and only if, it is connected and
reflexive.
Injective (also called left-unique)
For all x, y, z ∈ X, if xRy and zRy then x = z.
Functional (also called right-unique, right-definite
or univalent)
For all x, y, z ∈ X, if xRy and xRz then y = z.
Such a relation is called a partial function.
Serial (also called total or left-total)
For all x ∈ X, there exists some y ∈ X such that xRy.
Such a relation is called a multivalued function.
As an example, > is a serial relation over the integers.
But it is not a serial relation over the positive integers,
because there is no y in the positive integers such that 1 > y.
However, < is a serial relation over the positive integers,
the rational numbers and the real numbers.
Every reflexive relation is serial: for a given x, choose y = x.
Surjective (also called right-total or onto)
For all y ∈ Y, there exists an x ∈ X such that xRy.
Relations that satisfy combinations of the above properties are
useful,
and thus have received names by their own.
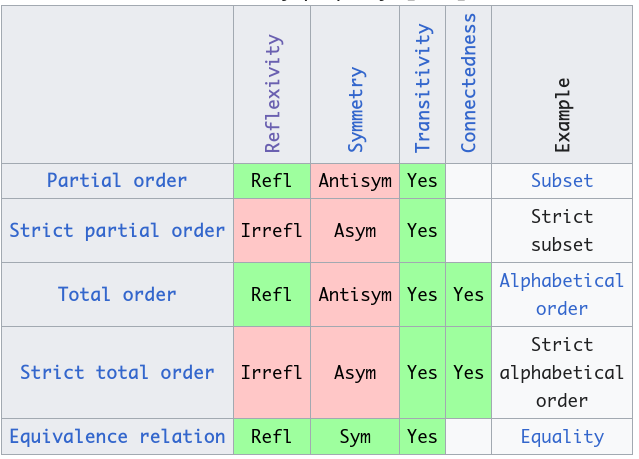
Equivalence relation
A relation that is reflexive, symmetric, and transitive.
It is also a relation that is symmetric, transitive, and serial,
since these properties imply reflexivity.
Summary of some standard relational operators:

Partial order
A relation that is reflexive, antisymmetric, and transitive.
Quasi order
A relation that is irreflexive and transitive.
Strict partial order
A relation that is irreflexive, asymmetric, and transitive.
Total order (linear)
A relation that is reflexive, antisymmetric, transitive and
connected.
Strict total order
A relation that is irreflexive, asymmetric, transitive and
connected.
Well order
A well order is a total (or linear) order that has a least
element;
furthermore, every subset of a well order must have a least
element.
The existence of a least element is significant,
because it provides a base case for recursive functions and for
inductive proofs.
Given a set S and a binary relation R over S, R is a well order,
if:
R is a linear order, and every subset of S, that is not empty, contains
a least element.
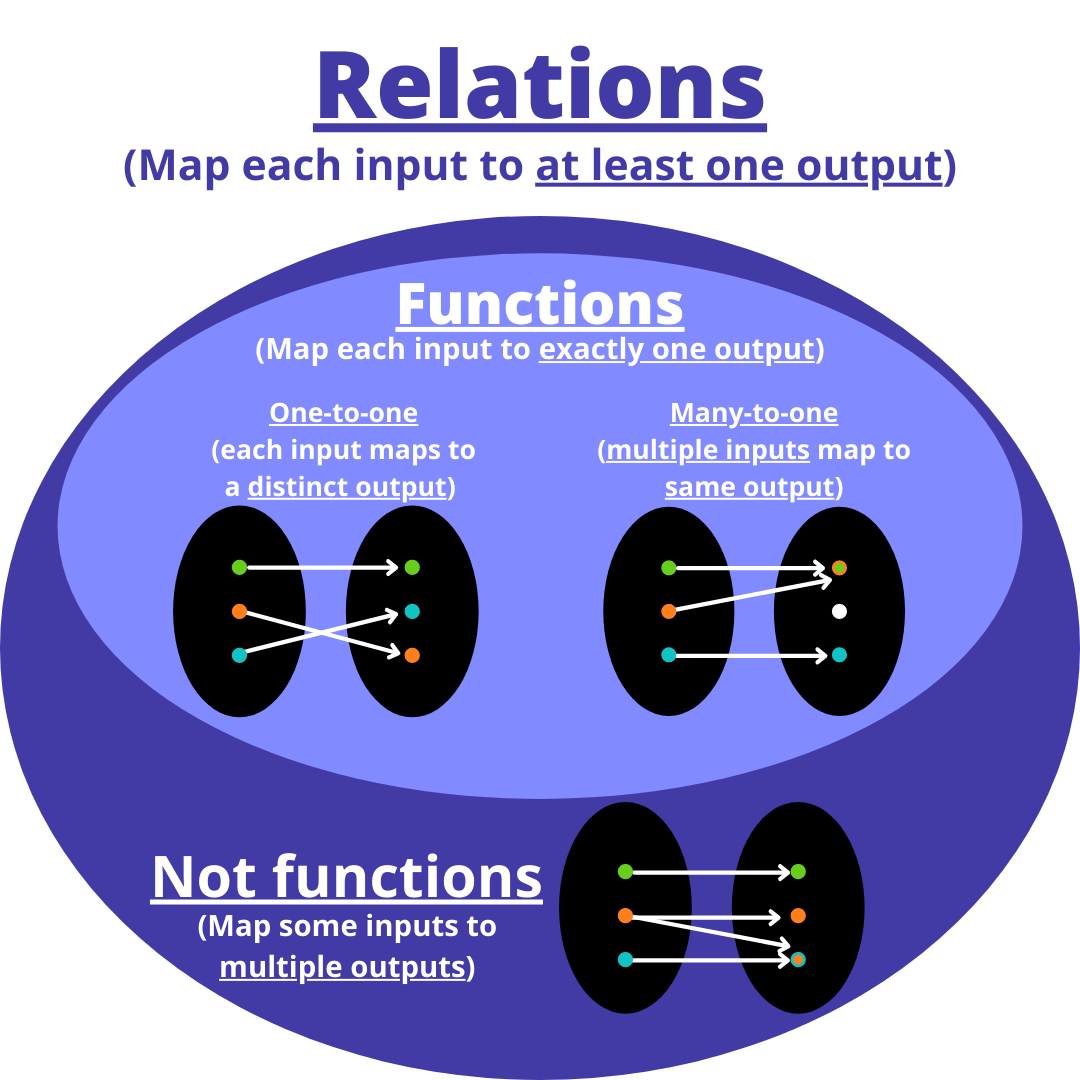
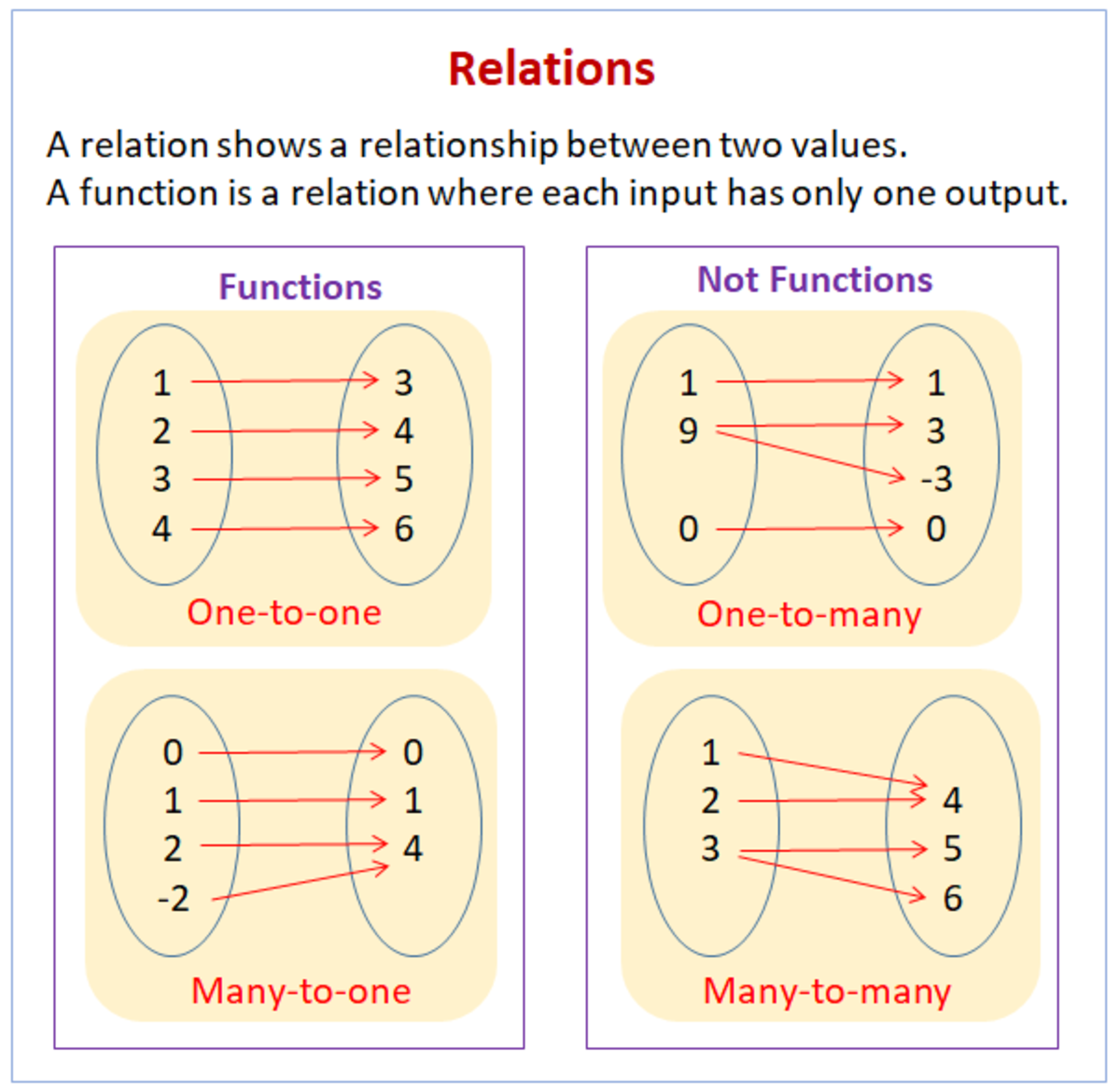
One-to-one
Injective and functional.
For example:
the green relation in the diagram is one-to-one,
but the red, blue and black ones are not.
One-to-many
Injective and not functional.
For example:
the blue relation in the diagram is one-to-many,
but the red, green and black ones are not.
Many-to-one
Functional and not injective.
For example:
the red relation in the diagram is many-to-one,
but the green, blue and black ones are not.
Many-to-many
Not injective nor functional.
For example:
the black relation in the diagram is many-to-many,
but the red, green and blue ones are not.
A function
A relation that is functional and total.
For example:
the red and green relations in the diagram are functions,
but the blue and black ones are not.
An injection
A function that is injective.
For example:
the green relation in the diagram is an injection,
but the red, blue and black ones are not.
A surjection
A function that is surjective.
For example:
the green relation in the diagram is a surjection,
but the red, blue and black ones are not.
A bijection
A function that is injective and surjective.
For example:
the green relation in the diagram is a bijection,
but the red, blue and black ones are not.
Union
If R and S are relations over X,
then R ∪ S = { (x, y) | xRy or xSy } is the union relation of R and
S.
The identity element of this operation is the empty relation.
For example, ≤ is the union of < and =, and ≥ is the union of >
and =.
Intersection
If R and S are relations over X,
then R ∩ S = { (x, y) | xRy and xSy } is the intersection relation of R
and S.
The identity element of this operation is the universal relation.
For example, “is a lower card of the same suit as” is the intersection
of:
“is a lower card than” and “belongs to the same suit as”.
Composition
If R and S are relations over X,
then S ∘ R = { (x, z) | there exists y ∈ X such that xRy and ySz }
(also denoted by R; S) is the relative product of R and S.
The identity element is the identity relation.
The order of R and S in the notation S ∘ R,
used here agrees with the standard notational order for composition of
functions.
For example,
the composition “is mother of” ∘ “is parent of” yields: “is maternal
grandparent of”,
while the composition “is parent of” ∘ “is mother of” yields: “is
grandmother of”.
For the former case, if x is the parent of y, and y is the mother of
z,
then x is the maternal grandparent of z.
We can think of a relation R :: A × B,
as taking us from a point x ∈ A, to a point y ∈ B,
assuming that (x, y) ∈ R.
Now suppose there is another relation S :: B × C,
and suppose that (y, z) ∈ S, where z ∈ C.
Using first R and then S, we get from x to z, via the intermediate point
y.
We could define a new relation,
that describes the effect of doing first R and then S.
This is called the composition of R and S,
and the notation for it is R; S.
Let R1 :: A × B be a relation from set A to set B,
and R2 :: B × C be a relation from set B to set C.
Their relational composition is defined as follows:
R1 ; R 2 ::A×C
R1 ; R2 ={(a, c) | a ∈ A ∧ c ∈ C ∧ (∃ b ∈ B. (a, b) ∈ R1 ∧ (b, c) ∈ R2
)}
The definition just says formally that:
R1 ; R2 consists of all the pairs (a, c),
such that there is an intermediate connecting point b.
This means that (a, b) ∈ R1 and (b, c) ∈ R2 .
Power
For a relation R, the nth power is the composition R; R; ···; R,
where R appears n times, and its notation is Rn.
Notice in particular that R2 = R; R, and R1 =
R.
It is also convenient to define R0 to be the identity
relation.
When a relation R is composed with itself n times,
producing Rn, a path of length n in R, from a to b,
causes there to be a single link (a, b) in the power relation
Rn.
Let A be a set and let R :: A × A be a relation defined over A.
The nth power of R, denoted Rn , is defined as follows:
R0 = {(a, a) | a ∈ A}
Rn+1 = Rn ; R
Converse
If R is a relation over sets X and Y,
then RT = { (y, x) | xRy } is the converse relation of R over Y and
X.
For example, = is the converse of itself, as is ≠,
and < and > are each other’s converse, as are ≤ and ≥.
Complement
If R is a relation over X,
then R = { (x, y) | x, y ∈ X and not xRy } (also denoted by R or ¬R) is
the complementary relation of R.
For example, = and ≠ are each other’s complement,
as are ⊆ and ⊈, ⊇ and ⊉, and ∈ and ∉, and,
for total orders, also < and ≥, and > and ≤.
Restriction
If R is a relation over X and S is a subset of X,
then R|S = { (x, y) | xRy and x, y ∈ S } is the restriction relation of
R to S.
The expression R|S = { (x, y) | xRy and x ∈ S } is the left-restriction
relation of R to S;
the expression R|S = { (x, y) | xRy and y ∈ S } is called the
right-restriction relation of R to S.
-- # Software Tools for Discrete Mathematics
module Stdm10Relations where
import Stdm06LogicOperators
import Stdm08SetTheory
-- # Chapter 10. Relations
type Relation a = Set (a, a)
type Digraph a = (Set a, Relation a)
-- | Returns the domain of a given set.
-- >>> domain [("a", 1), ("b", 2)]
-- ["a","b"]
domain :: (Eq a, Show a, Eq b, Show b) => Set (a, b) -> Set a
domain set =
if not (normalForm set)
then errfun "domain" set "set"
else map fst set
-- | Returns the codomain of a give set.
-- >>> codomain [("a", 1), ("b", 2)]
-- [1,2]
codomain :: (Eq a, Show a, Eq b, Show b) => Set (a, b) -> Set b
codomain set =
if not (normalForm set)
then errfun "codomain" set "set"
else map snd set
-- |
-- >>> isDigraph ([1..10], [(1,2),(3,4)])
-- True
isDigraph :: (Eq a, Show a) => Digraph a -> Bool
isDigraph (set, relation) =
normalForm set /\ normalForm relation
-- | The set and relations must be the same, to be the same digraph.
-- >>> digraphEq ([1..10], [(1,2),(3,4)]) ([1..4], [(1,2),(3,4)])
-- False
-- | The set and relations must be the same, to be the same digraph.
-- >>> digraphEq ([1..10], [(1,2),(3,4)]) ([1..10], [(1,2),(3,5)])
-- False
digraphEq :: (Eq a, Show a) => Digraph a -> Digraph a -> Bool
digraphEq digraph1 digraph2 =
if not (isDigraph digraph1)
then errfun "digraphEq" digraph1 "digraph"
else
if not (isDigraph digraph2)
then errfun "digraphEq" digraph2 "digraph"
else
let (set1, relation1) = digraph1
(set2, relation2) = digraph2
in (setEq set1 set2) /\ (setEq relation1 relation2)
-- | This relation only has reflexive links.
-- >>> isReflexive ([1,2], [(1,1),(2,2)])
-- True
-- | It may have some links that are not themselves reflixive.
-- >>> isReflexive ([1,2], [(1,1),(2,2),(1,2)])
-- True
isReflexive :: (Eq a, Show a) => Digraph a -> Bool
isReflexive digraph =
if not (isDigraph digraph)
then errfun "isReflexive" digraph "digraph"
else
let (set, relation) = digraph
in and [elem (e, e) relation | e <- set]
-- | Even one self-link makes the whole relation irreflexive:
-- >>> isIrreflexive ([1,2], [(1,1),(1,2)])
-- False
-- | Contains no self-links:
-- >>> isIrreflexive ([1,2], [(1,2)])
-- True
isIrreflexive :: (Eq a, Show a) => Digraph a -> Bool
isIrreflexive digraph =
if not (isDigraph digraph)
then errfun "isIrreflexive" digraph "digraph"
else
let (set, relation) = digraph
in [a | (a, b) <- relation, a == b && elem a set] == []
-- Note: a relation may be neither fully reflexive or irreflexive.
-- | All links must be mirrored.
-- >>> isSymmetric ([1,2], [(1,2),(2,1)])
-- True
isSymmetric :: (Eq a, Show a) => Digraph a -> Bool
isSymmetric digraph =
if not (isDigraph digraph)
then errfun "isSymmetric" digraph "digraph"
else
let (set, relation) = digraph
in and
[ (elem (a, b) relation) ==> (elem (b, a) relation)
| a <- set,
b <- set
]
-- | Can contain no symmetric links
-- >>> isAntisymmetric ([1,2], [(1,2),(2,2)])
-- True
isAntisymmetric :: (Eq a, Show a) => Digraph a -> Bool
isAntisymmetric digraph =
if not (isDigraph digraph)
then errfun "isAntisymmetric" digraph "digraph"
else
let (set, relation) = digraph
in and
[ ((elem (x, y) relation) /\ (elem (y, x) relation))
==> (x == y)
| x <- set,
y <- set
]
-- |
-- >>> isTransitive ([1,2,3], [(1,2),(2,3),(1,3)])
-- True
-- |
-- >>> isTransitive ([1,2,3], [(1,2),(2,3)])
-- False
isTransitive :: (Eq a, Show a) => Digraph a -> Bool
isTransitive digraph =
if not (isDigraph digraph)
then errfun "isTransitive" digraph "digraph"
else
let (set, relation) = digraph
in and
[ ((elem (x, y) relation) /\ (elem (y, z) relation))
==> (elem (x, z) relation)
| x <- set,
y <- set,
z <- set
]
-- |
-- >>> isReflexive lessThan_N100
-- False
-- |
-- >>> isIrreflexive lessThan_N100
-- True
-- |
-- >>> isSymmetric lessThan_N100
-- False
-- |
-- >>> isAntisymmetric lessThan_N100
-- True
lessThan_N100 :: Digraph Int
lessThan_N100 =
let set = [1 .. 100]
in (set, [(a, b) | a <- set, b <- set, a < b])
-- |
-- >>> isReflexive equals_N100
-- True
-- |
-- >>> isIrreflexive equals_N100
-- False
-- |
-- >>> isSymmetric equals_N100
-- True
-- |
-- >>> isAntisymmetric equals_N100
-- True
equals_N100 :: Digraph Int
equals_N100 =
let set = [1 .. 100]
in (set, [(a, b) | a <- set, b <- set, a == b])
-- |
-- >>> isReflexive greaterThan_N100
-- False
-- |
-- >>> isIrreflexive greaterThan_N100
-- True
-- |
-- >>> isSymmetric greaterThan_N100
-- False
-- |
-- >>> isAntisymmetric greaterThan_N100
-- True
greaterThan_N100 :: Digraph Int
greaterThan_N100 =
let set = [1 .. 100]
in (set, [(a, b) | a <- set, b <- set, a > b])
-- |
-- >>> isReflexive lessThanOrEq_N100
-- True
-- |
-- >>> isIrreflexive lessThanOrEq_N100
-- False
-- |
-- >>> isSymmetric lessThanOrEq_N100
-- False
-- |
-- >>> isAntisymmetric lessThanOrEq_N100
-- True
lessThanOrEq_N100 :: Digraph Int
lessThanOrEq_N100 =
let set = [1 .. 100]
in (set, [(a, b) | a <- set, b <- set, a < b \/ a == b])
-- |
-- >>> isReflexive greaterThanOrEq_N100
-- True
-- |
-- >>> isIrreflexive greaterThanOrEq_N100
-- False
-- |
-- >>> isSymmetric greaterThanOrEq_N100
-- False
-- |
-- >>> isAntisymmetric greaterThanOrEq_N100
-- True
greaterThanOrEq_N100 :: Digraph Int
greaterThanOrEq_N100 =
let set = [1 .. 100]
in (set, [(a, b) | a <- set, b <- set, a > b \/ a == b])
-- |
-- >>> isReflexive notEq_N100
-- False
-- |
-- >>> isIrreflexive notEq_N100
-- True
-- |
-- >>> isSymmetric notEq_N100
-- True
-- |
-- >>> isAntisymmetric notEq_N100
-- False
notEq_N100 :: Digraph Int
notEq_N100 =
let set = [1 .. 100]
in (set, [(a, b) | a <- set, b <- set, not (a == b)])
-- |
-- >>> relationalComposition [('a',1),('b',2)] [(1,"one"),(2,"two")]
-- [('a',"one"),('b',"two")]
relationalComposition ::
(Show a, Eq b, Show c, Show b, Eq c, Eq a) =>
Set (a, b) ->
Set (b, c) ->
Set (a, c)
relationalComposition set1 set2 =
if not (normalForm set1)
then errfun "relationalComposition" set1 "relation"
else
if not (normalForm set2)
then errfun "relationalComposition" set2 "relation"
else normalizeSet [(a, c) | (a, b) <- set1, (b', c) <- set2, b == b']
-- | A helper function for relationalPower below.
-- >>> equalityRelation [(1,2),(5,6)]
-- [((1,2),(1,2)),((5,6),(5,6))]
equalityRelation :: (Eq a, Show a) => Set a -> Relation a
equalityRelation set =
if not (normalForm set)
then errfun "equalityRelation" set "set"
else [(e, e) | e <- set]
-- |
-- >>> relationalPower (["Rolla","St. James","Cuba"], [("Rolla", "St. James"), ("St. James", "Cuba")]) 0
-- [("Rolla","Rolla"),("St. James","St. James"),("Cuba","Cuba")]
-- |
-- >>> relationalPower (["Rolla","St. James","Cuba"], [("Rolla", "St. James"), ("St. James", "Cuba")]) 1
-- [("Rolla","St. James"),("St. James","Cuba")]
-- |
-- >>> relationalPower (["Rolla","St. James","Cuba"], [("Rolla", "St. James"), ("St. James", "Cuba")]) 2
-- [("Rolla","Cuba")]
relationalPower :: (Eq a, Show a) => Digraph a -> Int -> Relation a
relationalPower digraph power =
if not (isDigraph digraph)
then errfun "relationalPower" digraph "digraph"
else relationalPowerLoop digraph power
where
relationalPowerLoop (set, relation) 0 =
equalityRelation set
relationalPowerLoop (set, relation) n =
relationalComposition
(relationalPowerLoop (set, relation) (n - 1))
relation
-- Closures: Derive standard relations from a smaller database.
-- The original database is the critical "information",
-- and the derivations can be re-computed.
-- |
-- >>> reflexiveClosure ([1,2,3], [(1,2),(2,3),(1,3)])
-- ([1,2,3],[(1,2),(2,3),(1,3),(1,1),(2,2),(3,3)])
reflexiveClosure :: (Eq a, Show a) => Digraph a -> Digraph a
reflexiveClosure digraph =
if not (isDigraph digraph)
then errfun "reflexiveClosure" digraph "digraph"
else
let (set, relation) = digraph
in (set, relation +++ (equalityRelation set))
-- | helper function for symmetricClosure
-- >>> inverse [(1,2),(2,3),(1,3)]
-- [(2,1),(3,2),(3,1)]
inverse :: Set (a, b) -> Set (b, a)
inverse set = [(b, a) | (a, b) <- set]
-- |
-- >>> symmetricClosure ([1,2,3], [(1,2),(2,3),(1,3)])
-- ([1,2,3],[(1,2),(2,3),(1,3),(2,1),(3,2),(3,1)])
symmetricClosure :: (Eq a, Show a) => Digraph a -> Digraph a
symmetricClosure digraph =
if not (isDigraph digraph)
then errfun "symmetricClosure" digraph "digraph"
else
let (set, relation) = digraph
in (set, relation +++ (inverse relation))
-- |
-- >>> transitiveClosure ([1,2,3], [(1,2),(2,3)])
-- ([1,2,3],[(1,2),(2,3),(1,3)])
transitiveClosure :: (Eq a, Show a) => Digraph a -> Digraph a
transitiveClosure digraph =
if not (isDigraph digraph)
then errfun "transitiveClosure" digraph "digraph"
else
let (set, relation) = digraph
len = length set
loop n power =
if (n > len)
then []
else
power
+++ ( loop
(n + 1)
(relationalComposition power relation)
)
in (set, loop 1 relation)
isPartialOrder :: (Eq a, Show a) => Digraph a -> Bool
isPartialOrder digraph =
if not (isDigraph digraph)
then errfun "isPartialOrder" digraph "digraph"
else
isReflexive digraph
/\ ( isAntisymmetric digraph
/\ isTransitive digraph
)
remTransArcs :: (Eq a, Show a) => Relation a -> Relation a
remTransArcs relation =
relation ~~~ [(x, z) | (x, y) <- relation, (y', z) <- relation, y == y']
remRelArcs :: (Eq a, Show a) => Relation a -> Relation a
remRelArcs relation = relation ~~~ [(x, y) | (x, y) <- relation, x == y]
remReflexTransArcs :: (Eq a, Show a) => Relation a -> Relation a
remReflexTransArcs relation =
remTransArcs (remRelArcs relation)
isWeakest :: (Eq a, Show a) => Relation a -> a -> Bool
isWeakest relation a =
if not (normalForm relation)
then errfun "isWeakest" relation "relation"
else and [a /= c | (b, c) <- remReflexTransArcs relation]
isGreatest :: (Eq a, Show a) => Relation a -> a -> Bool
isGreatest set a =
if not (normalForm set)
then errfun "isGreatest" set "relation"
else and [a /= b | (b, c) <- remReflexTransArcs set]
weakestSet :: (Eq a, Show a) => Digraph a -> Set a
weakestSet digraph =
if not (isDigraph digraph)
then errfun "weakestSet" digraph "digraph"
else
let (set, relation) = digraph
in filter (isWeakest relation) set
greatestSet :: (Eq a, Show a) => Digraph a -> Set a
greatestSet digraph =
if not (isDigraph digraph)
then errfun "greatestSet" digraph "digraph"
else
let (set, relation) = digraph
in filter (isGreatest relation) set
isQuasiOrder :: (Eq a, Show a) => Digraph a -> Bool
isQuasiOrder digraph =
if not (isDigraph digraph)
then errfun "isQuasiOrder" digraph "digraph"
else
isTransitive digraph
/\ isIrreflexive digraph
isChain :: (Eq a, Show a) => Set (a, a) -> Bool
isChain rel =
let loop [] = True
loop ((a, b) : ps) =
let new_rel = [pr | pr <- rel, not (pr == (a, b))]
in if (elem a (codomain new_rel) || elem b (domain new_rel))
then loop ps
else False
in loop rel
isLinearOrder :: (Eq a, Show a) => Digraph a -> Bool
isLinearOrder digraph =
if not (isDigraph digraph)
then errfun "isLinearOrder" digraph "digraph"
else
if not (isPartialOrder digraph)
then errfun "isLinearOrder" digraph "partial order"
else
let (set, relation) = digraph
in isChain (remReflexTransArcs relation)
removeFromRelation :: (Eq a, Show a) => a -> Set (a, a) -> Set (a, a)
removeFromRelation elt relation =
loop relation
where
loop [] = []
loop ((a, b) : relation) =
if ((elt == a) || (elt == b))
then loop relation
else (a, b) : loop relation
removeElt :: (Eq a, Show a) => a -> Digraph a -> Digraph a
removeElt elt (set, relation) =
( set ~~~ [elt],
removeFromRelation elt relation
)
topsort :: (Eq a, Show a) => Digraph a -> Set a
topsort digraph =
if not (isPartialOrder digraph)
then errfun "topsort" digraph "partial order"
else
let topsortLoop ([], relation) = []
topsortLoop (set, []) = []
topsortLoop digraph =
min_elt : topsortLoop (removeElt min_elt digraph)
where
min_elt = head (weakestSet digraph)
in topsortLoop digraph
isEquivalenceRelation :: (Eq a, Show a) => Digraph a -> Bool
isEquivalenceRelation digraph =
if not (isDigraph digraph)
then errfun "isEquivalenceRelation" digraph "digraph"
else
let (set, relation) = digraph
in ( isReflexive digraph
/\ (isSymmetric digraph /\ isTransitive digraph)
)module HL05REL where
import Data.List
import SetOrd
divisors :: Integer -> [(Integer, Integer)]
divisors n = [(d, quot n d) | d <- [1 .. k], rem n d == 0]
where
k = floor (sqrt (fromInteger n))
prime'' :: Integer -> Bool
prime'' = \n -> divisors n == [(1, n)]
divs :: Integer -> [Integer]
divs n = [d | d <- [1 .. n], rem n d == 0]
properDivs :: Integer -> [Integer]
properDivs n = init (divs n)
perfect :: Integer -> Bool
perfect n = sum (properDivs n) == n
type Rel a = Set (a, a)
domR :: (Ord a) => Rel a -> Set a
domR (Set r) = list2set [x | (x, _) <- r]
ranR :: (Ord a) => Rel a -> Set a
ranR (Set r) = list2set [y | (_, y) <- r]
idR :: (Ord a) => Set a -> Rel a
idR (Set xs) = Set [(x, x) | x <- xs]
totalR :: Set a -> Rel a
totalR (Set xs) = Set [(x, y) | x <- xs, y <- xs]
invR :: (Ord a) => Rel a -> Rel a
invR (Set []) = (Set [])
invR (Set ((x, y) : r)) = insertSet (y, x) (invR (Set r))
inR :: (Ord a) => Rel a -> (a, a) -> Bool
inR r (x, y) = inSet (x, y) r
complR :: (Ord a) => Set a -> Rel a -> Rel a
complR (Set xs) r =
Set [(x, y) | x <- xs, y <- xs, not (inR r (x, y))]
reflR :: (Ord a) => Set a -> Rel a -> Bool
reflR set r = subSet (idR set) r
irreflR :: (Ord a) => Set a -> Rel a -> Bool
irreflR (Set xs) r =
all (\pair -> not (inR r pair)) [(x, x) | x <- xs]
symR :: (Ord a) => Rel a -> Bool
symR (Set []) = True
symR (Set ((x, y) : pairs))
| x == y = symR (Set pairs)
| otherwise =
inSet (y, x) (Set pairs)
&& symR (deleteSet (y, x) (Set pairs))
transR :: (Ord a) => Rel a -> Bool
transR (Set []) = True
transR (Set s) = and [trans pair (Set s) | pair <- s]
where
trans (x, y) (Set r) =
and [inSet (x, v) (Set r) | (u, v) <- r, u == y]
infixr 5 @@
(@@) :: (Eq a) => Rel a -> Rel a -> Rel a
(Set r) @@ (Set s) =
Set (nub [(x, z) | (x, y) <- r, (w, z) <- s, y == w])
repeatR :: (Ord a) => Rel a -> Int -> Rel a
repeatR r n
| n < 1 = error "argument < 1"
| n == 1 = r
| otherwise = r @@ (repeatR r (n - 1))
r = Set [(0, 2), (0, 3), (1, 0), (1, 3), (2, 0), (2, 3)]
r2 = r @@ r
r3 = repeatR r 3
r4 = repeatR r 4
s = Set [(0, 0), (0, 2), (0, 3), (1, 0), (1, 2), (1, 3), (2, 0), (2, 2), (2, 3)]
test = (unionSet r (s @@ r)) == s
divides :: Integer -> Integer -> Bool
divides d n
| d == 0 = error "divides: zero divisor"
| otherwise = (rem n d) == 0
eq :: (Eq a) => (a, a) -> Bool
eq = uncurry (==)
lessEq :: (Ord a) => (a, a) -> Bool
lessEq = uncurry (<=)
inverse :: ((a, b) -> c) -> ((b, a) -> c)
inverse f (x, y) = f (y, x)
type Rel' a = a -> a -> Bool
emptyR' :: Rel' a
emptyR' = \_ _ -> False
list2rel' :: (Eq a) => [(a, a)] -> Rel' a
list2rel' xys = \x y -> elem (x, y) xys
idR' :: (Eq a) => [a] -> Rel' a
idR' xs = \x y -> x == y && elem x xs
invR' :: Rel' a -> Rel' a
invR' = flip
inR' :: Rel' a -> (a, a) -> Bool
inR' = uncurry
reflR' :: [a] -> Rel' a -> Bool
reflR' xs r = and [r x x | x <- xs]
irreflR' :: [a] -> Rel' a -> Bool
irreflR' xs r = and [not (r x x) | x <- xs]
symR' :: [a] -> Rel' a -> Bool
symR' xs r = and [not (r x y && not (r y x)) | x <- xs, y <- xs]
transR' :: [a] -> Rel' a -> Bool
transR' xs r =
and
[ not (r x y && r y z && not (r x z))
| x <- xs,
y <- xs,
z <- xs
]
unionR' :: Rel' a -> Rel' a -> Rel' a
unionR' r s x y = r x y || s x y
intersR' :: Rel' a -> Rel' a -> Rel' a
intersR' r s x y = r x y && s x y
reflClosure' :: (Eq a) => Rel' a -> Rel' a
reflClosure' r = unionR' r (==)
symClosure' :: Rel' a -> Rel' a
symClosure' r = unionR' r (invR' r)
compR' :: [a] -> Rel' a -> Rel' a -> Rel' a
compR' xs r s x y = or [r x z && s z y | z <- xs]
repeatR' :: [a] -> Rel' a -> Int -> Rel' a
repeatR' xs r n
| n < 1 = error "argument < 1"
| n == 1 = r
| otherwise = compR' xs r (repeatR' xs r (n - 1))
equivalenceR :: (Ord a) => Set a -> Rel a -> Bool
equivalenceR set r = reflR set r && symR r && transR r
equivalenceR' :: [a] -> Rel' a -> Bool
equivalenceR' xs r = reflR' xs r && symR' xs r && transR' xs r
modulo :: Integer -> Integer -> Integer -> Bool
modulo n = \x y -> divides n (x - y)
equalSize :: [a] -> [b] -> Bool
equalSize list1 list2 = (length list1) == (length list2)
type Part = [Int]
type CmprPart = (Int, Part)
expand :: CmprPart -> Part
expand (0, p) = p
expand (n, p) = 1 : (expand ((n - 1), p))
nextpartition :: CmprPart -> CmprPart
nextpartition (k, (x : xs)) = pack (x - 1) ((k + x), xs)
pack :: Int -> CmprPart -> CmprPart
pack 1 (m, xs) = (m, xs)
pack k (m, xs) =
if k > m
then pack (k - 1) (m, xs)
else pack k (m - k, k : xs)
generatePs :: CmprPart -> [Part]
generatePs p@(n, []) = [expand p]
generatePs p@(n, (x : xs)) =
(expand p : generatePs (nextpartition p))
part :: Int -> [Part]
part n
| n < 1 = error "part: argument <= 0"
| n == 1 = [[1]]
| otherwise = generatePs (0, [n])module Sol05 where
import Data.List
import HL05REL
import SetOrd
-- 5.52
-- To define restrictR, we need a version of intersectSet for sets as ordered lists:
intersectSet :: (Ord a) => Set a -> Set a -> Set a
intersectSet (Set []) set2 = Set []
intersectSet (Set (x : xs)) set2
| inSet x set2 = insertSet x (intersectSet (Set xs) set2)
| otherwise = intersectSet (Set xs) set2
-- Now computing the restriction of a relation R to a set A is a matter of intersecting R with A2 (the total relation on A):
restrictR :: (Ord a) => Set a -> Rel a -> Rel a
restrictR set rel = intersectSet (totalR set) rel
-- Note that it is assumed that the lists used in the representations of set and relation are ordered.
-- 5.53
rclosR :: (Ord a) => Rel a -> Rel a
rclosR r = unionSet r (idR background)
where
background = unionSet (domR r) (ranR r)
sclosR :: (Ord a) => Rel a -> Rel a
sclosR r = unionSet r (invR r)
-- 5.54
-- tclosR :: (Ord a) => Rel a -> Rel a
-- tclosR r
-- | transR r = r
-- | otherwise = tclosR (unionSet r (compR r r))
-- Bug with compR ?
-- 5.55
inDegree :: (Eq a) => Rel a -> a -> Int
inDegree (Set r) = \x -> length [y | (_, y) <- r, y == x]
outDegree :: (Eq a) => Rel a -> a -> Int
outDegree (Set r) = \x -> length [y | (y, _) <- r, y == x]
-- 5.56
sources :: (Eq a) => Rel a -> Set a
sources (Set r) =
Set
[ x | x <- union (map fst r) (map snd r), inDegree (Set r) x == 0, outDegree (Set r) x >= 1
]
sinks :: (Eq a) => Rel a -> Set a
sinks (Set r) =
Set
[ x | x <- union (map fst r) (map snd r), outDegree (Set r) x == 0, inDegree (Set r) x >= 1
]
-- 5.57
-- It is not hard to see that the successor relation:
-- S = {(n, m) ∈ Z | n + 1 = m} has the property that S ∪ S 2 6= S ∗ .
successor :: Rel' Int
successor = \n m -> n + 1 == m
rel = unionR' successor (repeatR' [0 .. 1000] successor 2)
-- Sol5> rel 1 3
-- True
-- Sol5> rel 1 4
-- False
-- This shows that rel is not the less-than relation on [1..1000].
-- 5.58
transClosure' :: [a] -> Rel' a -> Rel' a
transClosure' xs r
| transR' xs r = r
| otherwise = transClosure' xs (unionR' r (compR' xs r r))
-- 5.84
rclass :: Rel' a -> a -> [a] -> [a]
rclass r x ys = [y | y <- ys, r x y]
-- 5.106
bell :: Integer -> Integer
bell 0 = 1
bell n = sum [stirling n k | k <- [1 .. n]]
stirling :: Integer -> Integer -> Integer
stirling n 1 = 1
stirling n k
| n == k = 1
| otherwise = k * (stirling (n - 1) k) + stirling (n - 1) (k - 1)
-- 5.111
listPartition :: (Eq a) => [a] -> [[a]] -> Bool
listPartition xs xss =
all (`elem` xs) (concat xss)
&& all (`elem` (concat xss)) xs
&& listPartition' xss []
where
listPartition' [] _ = True
listPartition' ([] : xss) _ = False
listPartition' (xs : xss) domain
| intersect xs domain == [] = listPartition' xss (union xs domain)
| otherwise = False
-- 5.112
listpart2equiv :: (Ord a) => [a] -> [[a]] -> Rel a
listpart2equiv dom xss
| not (listPartition dom xss) = error "argument not a list partition"
| otherwise = list2set (concat (map f xss))
where
f xs = [(x, y) | x <- xs, y <- xs]
-- 5.114
equiv2listpart :: (Ord a) => Set a -> Rel a -> [[a]]
equiv2listpart s@(Set xs) r
| not (equivalenceR s r) = error "equiv2listpart: relation argument not an equivalence"
| otherwise = genListpart r xs
where
genListpart r [] = []
genListpart r (x : xs) = xclass : genListpart r (xs \\ xclass)
where
xclass = x : [y | y <- xs, inSet (x, y) r]
-- 5.115
equiv2part :: (Ord a) => Set a -> Rel a -> Set (Set a)
equiv2part s r = list2set (map list2set (equiv2listpart s r))
-- 5.125
coins :: [Int]
coins = [1, 2, 5, 10, 20, 50, 100, 200]
change :: Int -> [Int]
change n = moneyback n (n, [])
where
moneyback n (m, xs)
| m == 0 = xs
| n <= m && elem n coins = moneyback n (m - n, n : xs)
| otherwise = moneyback (n - 1) (m, xs)
-- 5.126
packCoins :: Int -> CmprPart -> CmprPart
packCoins k (m, xs)
| k == 1 = (m, xs)
| k <= m && elem k coins = packCoins k (m - k, k : xs)
| otherwise = packCoins (k - 1) (m, xs)
nextCpartition :: CmprPart -> CmprPart
nextCpartition (k, (x : xs)) = packCoins (x - 1) ((k + x), xs)
generateCps :: CmprPart -> [Part]
generateCps p@(n, []) = [expand p]
generateCps p@(n, (x : xs))
| elem x coins = (expand p : generateCps (nextCpartition p))
| otherwise = generateCps (nextCpartition p)
partC :: Int -> [Part]
partC n
| n < 1 = error "part: argument <= 0"
| n == 1 = [[1]]
| otherwise = generateCps (packCoins m (n - m, [m]))
where
m = maxInt (filter (<= n) coins)
maxInt [] = 0
maxInt (x : xs) = max x (maxInt xs)A dependency of the above set theory file:
Code-HRLMP/SetOrd.hs
module SetOrd
( Set (..),
emptySet,
isEmpty,
inSet,
subSet,
insertSet,
deleteSet,
powerSet,
takeSet,
(!!!),
list2set,
unionSet,
)
where
import Data.List (sort)
{-- Sets implemented as ordered lists without duplicates --}
newtype Set a = Set [a] deriving (Eq, Ord)
instance (Show a) => Show (Set a) where
showsPrec _ (Set s) str = showSet s str
showSet [] str = showString "{}" str
showSet (x : xs) str = showChar '{' (shows x (showl xs str))
where
showl [] str = showChar '}' str
showl (x : xs) str = showChar ',' (shows x (showl xs str))
emptySet :: Set a
emptySet = Set []
isEmpty :: Set a -> Bool
isEmpty (Set []) = True
isEmpty _ = False
inSet :: (Ord a) => a -> Set a -> Bool
inSet x (Set s) = elem x (takeWhile (<= x) s)
subSet :: (Ord a) => Set a -> Set a -> Bool
subSet (Set []) _ = True
subSet (Set (x : xs)) set = (inSet x set) && subSet (Set xs) set
insertSet :: (Ord a) => a -> Set a -> Set a
insertSet x (Set s) = Set (insertList x s)
insertList x [] = [x]
insertList x ys@(y : ys') = case compare x y of
GT -> y : insertList x ys'
EQ -> ys
_ -> x : ys
deleteSet :: (Ord a) => a -> Set a -> Set a
deleteSet x (Set s) = Set (deleteList x s)
deleteList x [] = []
deleteList x ys@(y : ys') = case compare x y of
GT -> y : deleteList x ys'
EQ -> ys'
_ -> ys
list2set :: (Ord a) => [a] -> Set a
list2set [] = Set []
list2set (x : xs) = insertSet x (list2set xs)
-- list2set xs = Set (foldr insertList [] xs)
powerSet :: (Ord a) => Set a -> Set (Set a)
powerSet (Set xs) =
Set (sort (map (\xs -> (list2set xs)) (powerList xs)))
powerList :: [a] -> [[a]]
powerList [] = [[]]
powerList (x : xs) =
(powerList xs)
++ (map (x :) (powerList xs))
takeSet :: (Eq a) => Int -> Set a -> Set a
takeSet n (Set xs) = Set (take n xs)
infixl 9 !!!
(!!!) :: (Eq a) => Set a -> Int -> a
(Set xs) !!! n = xs !! n
unionSet :: (Ord a) => Set a -> Set a -> Set a
unionSet (Set []) set2 = set2
unionSet (Set (x : xs)) set2 =
insertSet x (unionSet (Set xs) set2)