
https://en.wikipedia.org/wiki/Set-builder_notation#In_programming_languages
https://en.wikipedia.org/wiki/List_comprehension
Discrete Mathematics using a Comptuter (O’Donnell, Hall, Page) Chapter 8, 9
Discrete Mathematics with Applications - Metric Edition (Epp) Chapter 6
The Haskell Road to Logic, Math and Programming (Doets, van Eijck) Chapter 4, 11
https://www.cs.yale.edu/homes/aspnes/classes/202/notes.pdf Chapter 3
https://runestone.academy/ns/books/published/dmoi-4/sec_structures-sets.html
https://runestone.academy/ns/books/published/ads/chapter_1.html
https://runestone.academy/ns/books/published/ads/s-set-Notation-and-Relations.html
https://runestone.academy/ns/books/published/ads/s-basic_Set_Operations.html
https://runestone.academy/ns/books/published/ads/s-cartesian_Products_and_Power_Sets.html
https://runestone.academy/ns/books/published/ads/s-binary_Representation_of_Positive_Integers.html
https://runestone.academy/ns/books/published/ads/s-summation_Notation_and_Generalizations.html
https://runestone.academy/ns/books/published/ads/chapter_4.html
https://runestone.academy/ns/books/published/ads/s-proof-methods-sets.html
https://runestone.academy/ns/books/published/ads/s-laws-of-set-theory.html
https://runestone.academy/ns/books/published/ads/s-minsets.html
https://runestone.academy/ns/books/published/ads/s-duality-principle.html
https://runestone.academy/ns/books/published/DiscreteMathText/chapter6.html
https://runestone.academy/ns/books/published/DiscreteMathText/sets6-1.html
https://runestone.academy/ns/books/published/DiscreteMathText/propertiesofsets6-2.html
https://runestone.academy/ns/books/published/DiscreteMathText/algebraicsets6-3.html
https://en.wikipedia.org/wiki/Set_(mathematics)
https://en.wikipedia.org/wiki/Set_theory
https://en.wikipedia.org/wiki/Cartesian_product
https://hackage-content.haskell.org/package/containers-0.8/docs/Data-Set.html
https://haskell-containers.readthedocs.io/en/latest/set.html


Principle of Extensionality:
Sets that have the same elements are equal.
Elements – a, b, c, …
Sets – A, B, C, …
Empty set – { }, φ
Enumerated set – {e1, e2, …}
Set comprehension – {x | ···}
Cardinality – |A|
Member – x ∈ A
Not member – x \(\notin\) A
Subset – A ⊆ B
Not subset – A \(\not\subseteq\)
B
Proper subset – A ⊂ B
Not proper subset – A \(\not\subset\)
B
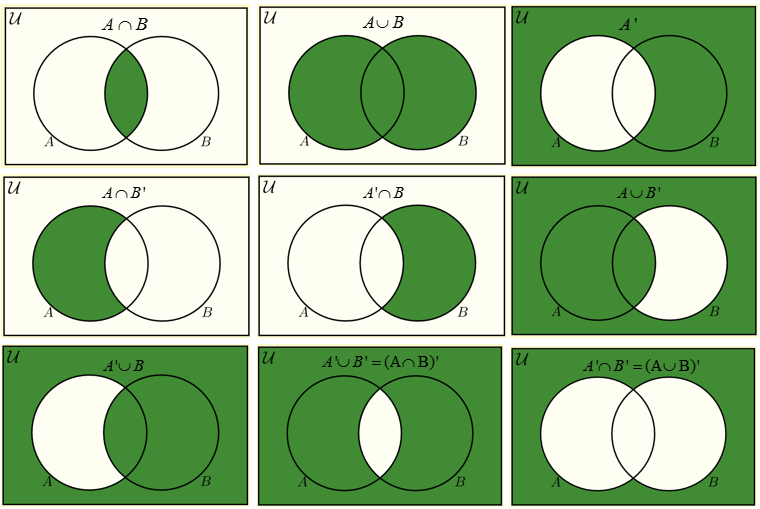
Union – A ∪ B
Intersection – A ∩ B
Set difference – A − B
Cross product – A × B
Set membership
x ∈ S x
is one of the elements of S
Cardinality
|S|
the number of distinct elements in the set S
Set enumeration
{x1, x2, …, xk}
the set containing elements x1, x2, …,
xk
Set abstraction
{x ∈ U : P(x)}
the set containing all x ∈ U for which P(x) is true;
U is the “universe” of candidate elements
Empty set
{} or ∅
the set containing no elements
Complement
∼S = {x ∈ U : x /∈ S}
the set of all elements in the universe U that aren’t in S;
U may be left implicit if it’s obvious from context
Let U be the universe of discourse and A be a set.
The complement of A, written A’, is the set U − A.
Union
S ∪ T = {x : x ∈ S or x ∈ T}
the set of all elements in either S or T (or both)
A ∪ B = {x | x ∈ A ∨ x ∈ B},
Intersection
S ∩ T = {x : x ∈ S and x ∈ T}
the set of all elements in both S and T
A ∩ B = {x | x ∈ A ∧ x ∈ B},
Set difference
S − T = {x : x ∈ S and x /∈ T}
the set of all elements in S but not in T
A − B = {x | x ∈ A ∧ x /∈ B}.
Set equality
S = T
every x ∈ S is also in T, and every x ∈ T is also in S
Let A and B be sets.
Then A = B if and only
if A ⊆ B and B ⊆ A.
union, intersection,
difference, complement
Subset
S ⊆ T
every x ∈ S is also in T
Let A and B be sets.
Then A ⊆ B if and only if
∀x.x ∈ A → x ∈ B.
Proper subset
S ⊂ T
S ⊆ T but S /= T
Let A and B be sets.
Then A ⊂ B if and only
if A ⊆ B and A /= B.
Superset
S ⊇ T
every x ∈ T is also in S
Proper superset
S ⊃ T
S ⊇ T but S /= T
Power set
P(S)
the set of all subsets of S
Let A be a set.
The powerset of A, written P (A),
is the set of all subsets of A:
P(A) = {S | S ⊆ A}
Cross product
A × B
Cartesian product of two sets A and B,
denoted A × B, is the set of all ordered pairs (a, b)
where a is an element of A,
and b is an element of B
In terms of set-builder notation,
that is A × B = { (a, b) ∣ a ∈ A and b ∈ B },
or in Haskell:
[(a, b) | a <- A, b <- B]

To compute the union (or intersection) of several sets in a more
general way,
we use operators that give the union (or intersection) of an arbitrary
number of sets,
rather than just two of them.
These operations are often called big union and big intersection:
One formulation follows:
Let C be a non-empty collection (set) of subsets of the universe
U.
Let I be a non-empty set,
and for each i ∈ I let Ai ⊆ C.
\[\bigcup_{i \in I} A_i = \{ x | \exists i \in I . x \in A_i\}\]
\[\bigcap_{i \in I} A_i = \{ x | \forall i \in I . x \in A_i\}\]
A second formulation follows:
Another way to say this is that:
if C is a set containing some sets,
then the set of all elements of the sets in C is:
\(\cup_{A \in C} A\),
and the set of elements that these sets in C have in common is:
\(\cap_{A \in C} A\).
\[\bigcup_{A \in C} A = \{ x | \exists A \in C . x \in A\}\]
\[\bigcap_{A \in C} A = \{ x | \forall A \in C . x \in A\}\]
Idempotent
A = A ∪ A
A = A ∩ A
Domination
A ∪ U = U
A ∩ ∅ = ∅
Identity
A ∪ ∅ = A
A ∩ U = A
Double complement
A = A’’
DeMorgan’s laws
(A ∪ B)’ = A’ ∩ B’
(A ∩ B)’ = A’ ∪ B’
Commutative laws
A ∪ B = B ∪ A
A ∩ B = B ∩ A
Associative laws
(A ∪ B) ∪ C = A ∪ (B ∪ C)
(A ∩ B) ∩ C = A ∩ (B ∩ C)
Distributive laws
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
Absorption laws
A ∪ (A ∩ B) = A
A ∩ (A ∪ B) = A
-- # Software Tools for Discrete Mathematics
module Stdm08SetTheory where
import Stdm06LogicOperators
-- # Chapter 8. Set Theory
type Set a = [a]
errfun :: (Show a) => String -> a -> String -> b
errfun f s msg = error (f ++ ": " ++ show s ++ " is not a " ++ msg)
-- | Note that subset does not reject non-sets
-- >>> subset [1,2] [1,2]
-- True
subset :: (Eq a, Show a) => Set a -> Set a -> Bool
subset set1 set2 =
foldr f True set1
where
f x sofar = if elem x set2 then sofar else False
-- | Note that properSubset does not reject non-sets
-- properSubset [1,2] [1,2,3]
-- True
properSubset :: (Eq a, Show a) => Set a -> Set a -> Bool
properSubset set1 set2 =
not (setEq set1 set2) /\ (subset set1 set2)
-- | Note that setEq does not reject non-sets
-- >>> setEq [1,2] [2,1]
-- True
setEq :: (Eq a, Show a) => Set a -> Set a -> Bool
setEq set1 set2 =
(set1 `subset` set2) /\ (set2 `subset` set1)
-- |
-- >>> normalForm [1,1,2,2,3,3]
-- False
normalForm :: (Eq a, Show a) => [a] -> Bool
normalForm set = length (normalizeSet set) == length set
-- |
-- >>> normalizeSet [1,1,2,2,3,3]
-- [1,2,3]
normalizeSet :: (Eq a) => [a] -> Set a
normalizeSet elts =
foldr f [] elts
where
f x sofar =
if x `elem` sofar then sofar else x : sofar
-- | Union
-- >>> [1,2] +++ [2,3]
-- [1,2,3]
infix 3 +++
(+++) :: (Eq a, Show a) => Set a -> Set a -> Set a
(+++) set1 set2 =
if not (normalForm set1)
then errfun "+++" set1 "set"
else
if not (normalForm set2)
then errfun "+++" set2 "set"
else normalizeSet (set1 ++ set2)
-- | Intersection
-- >>> [1,2] *** [2,3]
-- [2]
infix 4 ***
(***) :: (Eq a, Show a) => Set a -> Set a -> Set a
(***) set1 set2 =
if not (normalForm set1)
then errfun "***" set1 "set"
else
if not (normalForm set2)
then errfun "***" set2 "set"
else [x | x <- set1, (x `elem` set2)]
-- | Difference
-- >>> [1,2] ~~~ [2,3]
-- [1]
infix 4 ~~~
(~~~) :: (Eq a, Show a) => Set a -> Set a -> Set a
(~~~) set1 set2 =
if not (normalForm set1)
then errfun "~~~" set1 "set"
else
if not (normalForm set1)
then errfun "~~~" set2 "set"
else [x | x <- set1, not (x `elem` set2)]
-- | Complement
-- >>> [1..10] ~~~ [1]
-- [2,3,4,5,6,7,8,9,10]
infix 5 !!!
(!!!) :: (Eq a, Show a) => Set a -> Set a -> Set a
(!!!) u a =
if not (normalForm u)
then errfun "!!!" u "set"
else
if not (normalForm a)
then errfun "!!!" a "set"
else u ~~~ a
-- |
-- >>> powerset [1..3]
-- [[1,2,3],[1,2],[1,3],[1],[2,3],[2],[3],[]]
powerset :: (Eq a, Show a) => Set a -> Set (Set a)
powerset set =
if not (normalForm set)
then errfun "powerset" set "set"
else powersetLoop set
where
powersetLoop [] = [[]]
powersetLoop (e : set) =
let setSoFar = powersetLoop set
in [e : s | s <- setSoFar] ++ setSoFar
-- |
-- >>> crossproduct ["a","b"] [1,2,3]
-- [("a",1),("a",2),("a",3),("b",1),("b",2),("b",3)]
crossproduct ::
(Eq a, Show a, Eq b, Show b) =>
Set a ->
Set b ->
Set (a, b)
crossproduct set1 set2 =
if not (normalForm set1)
then errfun "crossproduct" set1 "set"
else
if not (normalForm set2)
then errfun "crossproduct" set2 "set"
else [(a, b) | a <- set1, b <- set2]Code-DMUC/Stdm09InductiveSets.hs
-- # Software Tools for Discrete Mathematics
module Stdm09InductiveSets where
-- # Chapter 9. Inductively defined setsmodule HL04STAL where
import DB
import Data.List
-- | The infinite set of natural numbers:
-- >>> take 10 naturals
-- [0,1,2,3,4,5,6,7,8,9]
naturals = [0 ..]
-- | The infinite set of even numbers:
-- >>> take 10 evens1
-- [0,2,4,6,8,10,12,14,16,18]
evens1 = [n | n <- naturals, even n]
-- | The infinite set of odd numbers:
-- >>> take 10 odds1
-- [1,3,5,7,9,11,13,15,17,19]
odds1 = [n | n <- naturals, odd n]
-- | The infinite set of even numbers:
-- >>> take 10 evens2
-- [0,2,4,6,8,10,12,14,16,18]
evens2 = [2 * n | n <- naturals]
-- | A finite set of squares:
-- >>> take 10 small_squares1
-- [0,1,4,9,16,25,36,49,64,81]
small_squares1 = [n ^ 2 | n <- [0 .. 999]]
-- | A finite set of squares:
-- >>> take 10 small_squares2
-- [0,1,4,9,16,25,36,49,64,81]
small_squares2 = [n ^ 2 | n <- naturals, n < 1000]
-- Here is a simple example of a program for which no proof of termination exists:
run :: Integer -> [Integer]
run n
| n < 1 = error "argument not positive"
| n == 1 = [1]
| even n = n : run (div n 2)
| odd n = n : run (3 * n + 1)
-- | Infinite set of ones, recursively defined:
-- >>> take 10 ones
-- [1,1,1,1,1,1,1,1,1,1]
ones = 1 : ones
-- See DB.hs for an example database:
characters = nub [x | ["play", _, _, x] <- db]
movies = [x | ["release", x, _] <- db]
actors = nub [x | ["play", x, _, _] <- db]
directors = nub [x | ["direct", x, _] <- db]
dates = nub [x | ["release", _, x] <- db]
universe = nub (characters ++ actors ++ directors ++ movies ++ dates)
direct = [(x, y) | ["direct", x, y] <- db]
act = [(x, y) | ["play", x, y, _] <- db]
play = [(x, y, z) | ["play", x, y, z] <- db]
release = [(x, y) | ["release", x, y] <- db]
charP = \x -> elem x characters
actorP = \x -> elem x actors
movieP = \x -> elem x movies
directorP = \x -> elem x directors
dateP = \x -> elem x dates
actP = \(x, y) -> elem (x, y) act
releaseP = \(x, y) -> elem (x, y) release
directP = \(x, y) -> elem (x, y) direct
playP = \(x, y, z) -> elem (x, y, z) play
q1 = [x | x <- actors, directorP x]
q2 = [(x, y) | (x, y) <- act, directorP x]
q3 = [(x, y, z) | (x, y) <- direct, (y, z) <- release]
q4 = [(x, y, z) | (x, y) <- direct, (u, z) <- release, y == u]
q5 = [(x, y) | (x, y) <- direct, (u, "1995") <- release, y == u]
q6 =
[ (x, y, z) | (x, y) <- direct, (u, z) <- release, y == u, z > "1995"
]
q7 = [x | ("Kevin Spacey", x) <- act]
q8 = [x | (x, y) <- release, y > "1997", actP ("William Hurt", x)]
q9 = q1 /= []
q10 = [x | ("Woody Allen", x) <- direct] /= []
q10' = directorP "Woody Allen"
-- Basic Set functions:
elem' :: (Eq a) => a -> [a] -> Bool
elem' x [] = False
elem' x (y : ys)
| x == y = True
| otherwise = elem' x ys
addElem :: a -> [[a]] -> [[a]]
addElem x = map (x :)
powerList :: [a] -> [[a]]
powerList [] = [[]]
powerList (x : xs) = (powerList xs) ++ (map (x :) (powerList xs))
data S = Void deriving (Eq, Show)
empty :: [S]
empty = []
display :: Int -> String -> IO ()
display n str = putStrLn (display' n 0 str)
where
display' _ _ [] = []
display' n m (x : xs)
| n == m = '\n' : display' n 0 (x : xs)
| otherwise = x : display' n (m + 1) xsA dependency of the above set theory file:
Code-HRLMP/DB.hs
module Sol04 where
import Data.List
import HL04STAL
import SetEq
-- 4.44
-- The definition could run like this:
-- L<K :≡ |L| < |K|
-- ∨ (|L| = |K|
-- ∧∃x, xs, y, ys (L = x : xs ∧ K = y : ys ∧ (x < y ∨ (x = y ∧ xs < ys)))).
compare' :: (Ord a) => [a] -> [a] -> Ordering
compare' [] [] = EQ
compare' (x : xs) (y : ys)
| length (x : xs) < length (y : ys) = LT
| length (x : xs) > length (y : ys) = GT
| otherwise = compare (x : xs) (y : ys)
-- And here is how it compares with the standard implementation of compare:
-- Sol4> compare [1,3] [1,2,3]
-- GT
-- Sol4> compare’ [1,3] [1,2,3]
-- LT
-- Sol4> compare [1,3] [1,2]
-- GT
-- Sol4> compare’ [1,3] [1,2]
-- GT
-- 4.46 Since reverse is predefined, we call our version reverse'.
reverse' :: [a] -> [a]
reverse' [] = []
reverse' (x : xs) = reverse' xs ++ [x]
-- 4.47
splitList :: [a] -> [([a], [a])]
splitList [x, y] = [([x], [y])]
splitList (x : y : zs) = ([x], (y : zs)) : addLeft x (splitList (y : zs))
where
addLeft u [] = []
addLeft u ((vs, ws) : rest) = (u : vs, ws) : addLeft u rest
-- A neater version results when we avail ourselves of the map function:
split :: [a] -> [([a], [a])]
split [x, y] = [([x], [y])]
split (x : y : zs) =
([x], (y : zs)) : (map (\(us, vs) -> ((x : us), vs)) (split (y : zs)))
-- 4.48
q11 = [y | (x, y) <- act, x == "Robert De Niro" || x == "Kevin Spacey"]
-- 4.49
q12 =
nub
( [y | ("Quentin Tarantino", y) <- act, releaseP (y, "1994")]
++ [y | ("Quentin Tarantino", y) <- direct, releaseP (y, "1994")]
)
-- 4.50
q13 = [x | (x, y) <- release, y > "1997", not (actP ("William Hurt", x))]
-- 4.51
difference :: (Eq a) => [a] -> [a] -> [a]
difference xs [] = xs
difference xs (y : ys) = difference (delete y xs) ys
-- 4.53
genUnion :: (Eq a) => [[a]] -> [a]
genUnion [] = []
genUnion [xs] = xs
genUnion (xs : xss) = union xs (genUnion xss)
genIntersect :: (Eq a) => [[a]] -> [a]
genIntersect [] = error "list of lists should be non-empty"
genIntersect [xs] = xs
genIntersect (xs : xss) = intersect xs (genIntersect xss)
-- 4.54
unionSet :: (Eq a) => Set a -> Set a -> Set a
unionSet (Set []) set2 = set2
unionSet (Set (x : xs)) set2 =
insertSet x (unionSet (Set xs) (deleteSet x set2))
intersectSet :: (Eq a) => Set a -> Set a -> Set a
intersectSet (Set []) set2 = Set []
intersectSet (Set (x : xs)) set2
| inSet x set2 = insertSet x (intersectSet (Set xs) set2)
| otherwise = intersectSet (Set xs) set2
differenceSet :: (Eq a) => Set a -> Set a -> Set a
differenceSet set1 (Set []) = set1
differenceSet set1 (Set (y : ys)) =
differenceSet (deleteSet y set1) (Set ys)
-- 4.55
-- insertSet will now have to insert an item at the right position to keep the underlying list sorted.
-- This can be done in terms of an auxiliary function insertList, as follows:
insertSet' :: (Ord a) => a -> Set a -> Set a
insertSet' x (Set s) = Set (insertList x s)
insertList x [] = [x]
insertList x ys@(y : ys') = case compare x y of
GT -> y : insertList x ys'
EQ -> ys
_ -> x : ys
-- 4.56
-- The only thing that is needed is a small patch in the function showSet, like this:
showSet [] str = showString "0" str
showSet (x : xs) str = showChar ' ' (shows x (showl xs str))
where
showl [] str = showChar ' ' str
showl (x : xs) str = showChar ',' (shows x (showl xs str))A dependency of the above set theory file:
Code-HRLMP/SetEq.hs
module SetEq
( Set (..),
emptySet,
isEmpty,
inSet,
subSet,
insertSet,
deleteSet,
powerSet,
takeSet,
list2set,
(!!!),
)
where
import Data.List (delete)
{-- Sets implemented as unordered lists without duplicates --}
newtype Set a = Set [a]
instance (Eq a) => Eq (Set a) where
set1 == set2 = subSet set1 set2 && subSet set2 set1
instance (Show a) => Show (Set a) where
showsPrec _ (Set s) str = showSet s str
showSet [] str = showString "{}" str
showSet (x : xs) str = showChar '{' (shows x (showl xs str))
where
showl [] str = showChar '}' str
showl (x : xs) str = showChar ',' (shows x (showl xs str))
emptySet :: Set a
emptySet = Set []
isEmpty :: Set a -> Bool
isEmpty (Set []) = True
isEmpty _ = False
inSet :: (Eq a) => a -> Set a -> Bool
inSet x (Set s) = elem x s
subSet :: (Eq a) => Set a -> Set a -> Bool
subSet (Set []) _ = True
subSet (Set (x : xs)) set = (inSet x set) && subSet (Set xs) set
insertSet :: (Eq a) => a -> Set a -> Set a
insertSet x (Set ys)
| inSet x (Set ys) = Set ys
| otherwise = Set (x : ys)
deleteSet :: (Eq a) => a -> Set a -> Set a
deleteSet x (Set xs) = Set (delete x xs)
list2set :: (Eq a) => [a] -> Set a
list2set [] = Set []
list2set (x : xs) = insertSet x (list2set xs)
powerSet :: (Eq a) => Set a -> Set (Set a)
powerSet (Set xs) = Set (map (\xs -> (Set xs)) (powerList xs))
powerList :: [a] -> [[a]]
powerList [] = [[]]
powerList (x : xs) = (powerList xs) ++ (map (x :) (powerList xs))
takeSet :: (Eq a) => Int -> Set a -> Set a
takeSet n (Set xs) = Set (take n xs)
infixl 9 !!!
(!!!) :: (Eq a) => Set a -> Int -> a
(Set xs) !!! n = xs !! n