Motivation and the trouble
What is a constrained problem?
Evolutionary constraint handling
A selection of related work
Conclusions, observations, and suggestions
Why bother about constraints?
Practical relevance:
a great deal of practical problems are constrained.
Theoretical challenge:
a great deal of intractable problems (NP-hard etc.) are constrained.
Why try with evolutionary algorithms?
EAs show a good ratio of (implementation) effort/performance.
EAs are acknowledged as good solvers for tough problems.
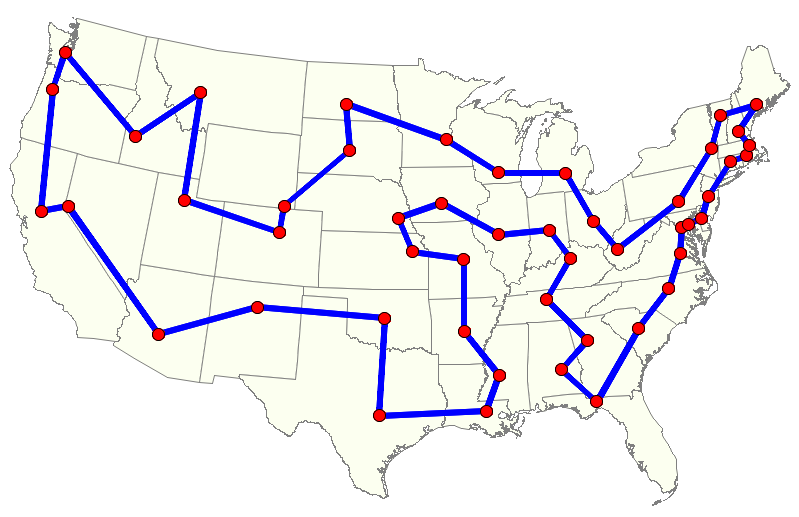
Consider the Traveling Salesman Problem for n cities, C = {city 1 , … , city n }
If we define the search space as
S = C n , then we need a constraint requiring uniqueness of each city in an element of S
S = {permutations of C}, then we need no additional constraint.
The notion ‘constrained problem’ depends on what we take as search space
_ _ standard
mutation if for all x 1 , … , x
n , if_ _ standard
crossover if for all x 1 , … , x
n , y 1 , … , y n
, ifFree search space: S = D 1 … D n
one assumption on D i : if it is continuous, it is convex
the restriction s i D i is not a constraint, it is the definition of the domain of the i-th variable
membership of S is coordinate-wise, hence a free search space allows free search
A problem can be defined through
an objective function (to be optimized)
constraints (to be satisfied)
| Objective Function | ||
|---|---|---|
| Constraints | Yes | No |
| Yes | Constrained optimization problem | Constraint satisfaction problem |
| No | Free optimization problem | No Problem |
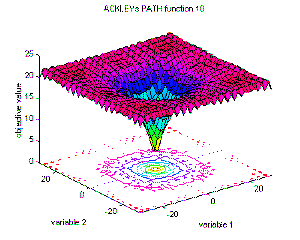
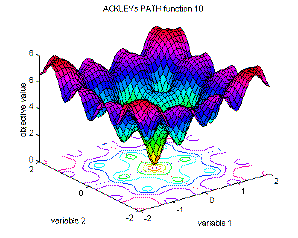
Free Optimization Problem: S, f, •
S is a free search space
f is a (real valued) objective function on S
Solution of an FOP: s S such that f (s) is optimal in S
FOPs are ‘easy’, in the sense that:
it’s ‘only’ optimizing, no constraints and
EAs have a basic instinct for optimization
Ackley function

Constraint Satisfaction Problem: S, •, Φ
S is a free search space
Φ is a formula (Boolean function on S)
Φ is the feasibility condition
S Φ = {s S | Φ(s) = true} is the feasible search space
Solution of a CSP:
s S such that Φ(s) = true (s is feasible)
Φ is typically given by a set (conjunction) of constraints
c i = c i (x j1 , … , x jni ), where n i is the arity of c i
c i D j1 … D
jni _ _ is also a common
notation _ _
FACTS :
The general CSP is NP-complete
Every CSP is equivalent with a binary CSP, where all n i 2
Constraint density and constraint tightness are parameters that determine how hard an instance is
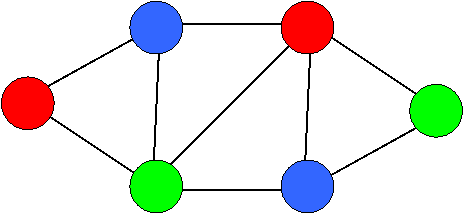
Graph 3-coloring problem:
G = (N, E), E N N , |N| = n
S = D n , D = {1, 2, 3}
Φ(s) = Λ e E c e (s), where
c e (s) = true iff e = (k, l) and s k s l
Constrained Optimization Problem: S, f, Φ
S is a free search space
f is a (real valued) objective function on S
Φ is a formula (Boolean function on S)
Solution of a COP:
s S Φ such that f(s) is optimal in S Φ
Travelling salesman problem
S = C n , C = {city 1 , … , city n }
Φ(s) = true i, j {1, … , n} i j s i s j
f(s) =
EAs need an f to optimize S, •, Φ must be transformed first to a
FOP: S, •, Φ S, f, • or
COP: S, •, Φ S, f, Ψ
The transformation must be (semi-)equivalent, i.e. at least:
f (s) is optimal in S Φ(s)
ψ (s) and f (s) is optimal in S Φ(s)
‘Constraint handling’ interpreted as ‘constraint transformation’
Case 1: CSP FOP
All constraints are handled indirectly , i.e., Φ is transformed into f and later they are solved by `simply’ optimizing in S, f, •
Case 2: CSP COP
Some constraints handled indirectly (those transformed into f)
Some constraints handled directly (those remaining constraints in ψ)
In the latter case we also have ‘constraint handling’ in the sense of ‘treated during the evolutionary search’
Constraint handling has two meanings:
how to transform the constraints in Φ into f, respectively f, ψ before applying an EA
how to enforce the constraints in S, f, Φ while running an EA
Case 1: constraint handling only in the 1st sense (pure penalty approach)
Case 2: constraint handling in both senses
In Case 2 the question
‘How to solve CSPs by EAs’
transforms to
‘How to solve COPs by EAs’
Note: always needed
for all constraints in Case 1
for some constraints in Case 2
Some general options
penalty for violated constraints
penalty for wrongly instantiated variables
estimating distance/cost to feasible solution
Notation:
c i constraints, i = {1, … , m}
v j variables, j = {1, … , n}
C j is the set of constraints involving variable v j
Sc = {z D j1 … D jk
_ _ | c(z) = true} is the
projection of c, if v j1 , … , v
jk are the var’s of c
d(s, S c ) := min{d(s, z) | z 2 S c } is the distance of s S from S c (s is projected too)
Observe that for each option:
PRO’s of indirect constraint handling:
conceptually simple, transparent
problem independent
reduces problem to ‘simple’ optimization
allows user to tune on his/her preferences by weights
allows EA to tune fitness function by modifying weights during the search
CON’s of indirect constraint handling:
loss of info by packing everything in a single number
said not to work well for sparse problems
Options:
eliminating infeasible candidates (very inefficient, hardly practicable)
repairing infeasible candidates
preserving feasibility by special operators
(requires feasible initial population
decoding, i.e. transforming the search space
(allows usual representation and operators)
PRO’s of direct constraint handling:
it works well (except eliminating)
CON’s of direct constraint handling:
problem specific
no guidelines