
“The formulation of the problem is often more essential than
its solution.”
-Albert Einstein
In EC, the representation is hard,
but that’s actually a good thing!
Cover the role of representation and variation operators.
Review the most common representation of genomes:
You don’t have to stick to the common representation schemes.
One can used hybrid, custom, and mixed representations and
operators,
depending on the problem.


The first stage of building an EA and most cognitively difficult one:
Choose the correct representation for the
problem.
It’s not the most computationally difficult (that’s often fitness for
large pop).
With a given representation,
one must also choose variation operators:
Mutation and Crossover
The type of variation operators needed depends on chosen
representation!
https://en.wikipedia.org/wiki/Mutation_(genetic_algorithm)
Mutation uses only one parent and creates one child.
Applies some kind of randomized change to the representation
(genotype).
The form taken depends on the choice of encoding used.
One usually also chooses an associated parameter,
which is introduced to regulate the intensity or magnitude of
mutation.
Depending on the given implementation, this can be:
mutation step size, etc.
mutation probability,
mutation rate,
No matter the representation, there is usually a measure of mutation
rate, pm.
Usually mutation rate (or quantity) is low.
For this lecture, we concentrate on the choice of operators,
rather than of parameters.
Parameters can make a significant difference in the behavior of the
evolutionary algorithm.
This is discussed in more depth later in the class:
ParameterTuning.html
ParameterControl.html
https://en.wikipedia.org/wiki/Crossover_(genetic_algorithm)
From the information contained within two (or more) parent
solutions,
a new individual solution is created.
Different branches of EC historically emphasized different variation
operators.
As these came together under the umbrella of evolutionary
algorithms,
this emphasis prompted a great deal of debate.
A lot of research activity has focused on recombination,
as the primary mechanism for creating diversity.
Mutation is sometimes considered as a background search operator.
Combining partial solutions via recombination distinguishes EAs from
other global optimization algorithms.
The term recombination has come to be used for the more general
case.
Early authors used the term crossover,
motivated by the biological analogy to meiosis.
Therefore we will occasionally use the terms interchangeably.
Crossover tends to refer to the most common two-parent case.
Recombination operators are usually applied probabilistically,
according to a crossover rate pc which defines whether
recombination happens.
Usually two parents are selected,
and with with probability pc
two offspring are created via recombination of the two parents.
Or, with probability 1 - pc
simply copy the parents,
Usually recombination rate (or quantity) is high.
Discuss:
Why can recombination rate be high, but mutation rate not?
One of the earliest representations.
Genotype consists of a string of binary digits.
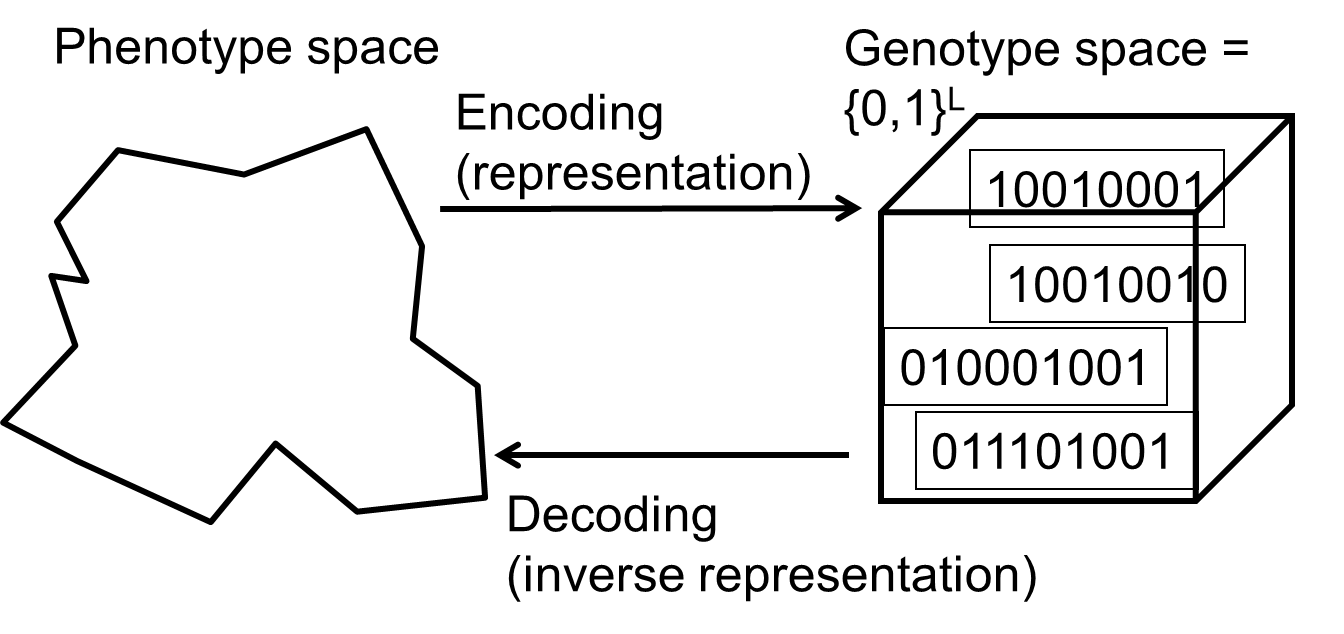
In choosing the genotype-phenotype mapping for a specific problem,
one should ideally make sure that the encoding allows both:
For some problems, particularly those concerning Boolean
decision variables,
the genotype-phenotype mapping is natural.
Using 0-1 bit-strings to encode non-binary information is usually a
mistake,
and better results can be obtained by using the integer, real-valued, or
other representations directly!
As an extreme example, one could mutate a binary code file using 0s
and 1s,
but the probability that you generate valid code is near 0!
It’s better to use Lisp strings!
Why?
Constraints are best specified at the level of abstraction you are
searching at!
Like with n-queens, or knapsack, we want to reduce the search space in
choosing our encoding.
Choosing a representation at too high a level of abstraction can make
the solution unreachable.
Choosing a representation at too low a level of abstraction can
unnecessarily increase our search space.
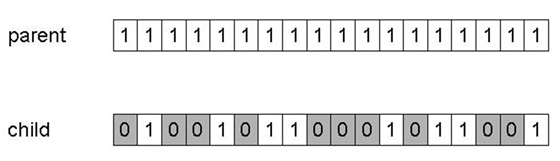
The most common mutation operator for binary encodings considers each
gene (position/bit) separately,
and allows each bit to flip (i.e., from 1 to 0 or 0 to 1).
Probability of mutation at each gene is pm,
also called the mutation rate.
Most binary coded GAs use mutation rates in a parameterized range,
such that on average between one gene per generation and one gene per
offspring is mutated.
Typically mutation rate is between 1/pop_size and
1/chromosome_length.
Cautionary note:
If you choose a binary representation when you should have chosen a
higher level representation,
mutation can cause variable effect!
e.g., If the goal is to evolve an integer number,
you would like to have equal probabilities of changing a 7 into an 8 or
a 6.
However, changing 0111 to 1000 requires four bit-flips while changing it
to 0110 takes just one.
Thus, the probability of changing 7 to 8 is much less than changing 7 to
6.
Use gray coding to fix such issues,
or just use a different interpretation or representation entirely…
Q: Which do you want more:
one good individual, or
a good population?
A: If one good individual is desired, then choose slightly higher
mutation rate
A: If a population is desired, then choose slightly lower mutation
rate
What if you’re:
losing diversity?
not converging?
These are all parameter tuning issues for later!
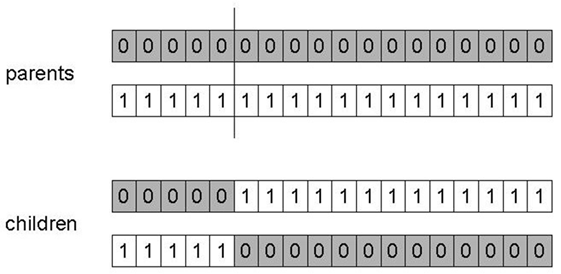
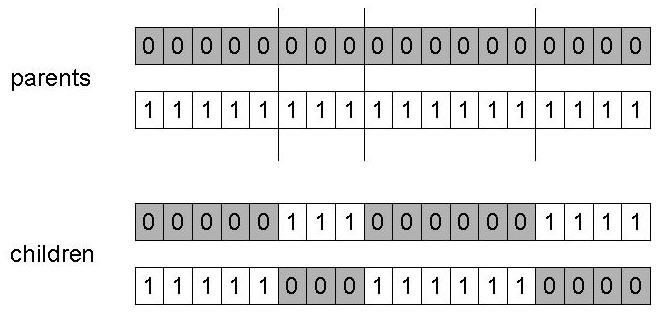
Choose a random point on the two parents,
with length l, and random position r:
r = random(1, l -1)
This limit keeps it away from the far ends.
Split parents at this crossover point.
Create children by exchanging tails.
Typically in range of probability:
pc = [0.6, 0.9]
Why do we need other crossover(s)?
Performance with 1-point crossover depends on the order that variables
occur in the representation.
It is more likely to keep together genes that are near each other.
Side note:
In biology, this is also true!
Genes close by each other are likely inherited together.
This is actually how we first started mapping chromosomes!
1-point can never keep together genes from opposite ends of
string.
This is also true for odd n-point crossover (below).
This is known as Positional Bias.
Biases like this can be both good and bad!
If we know about the structure of our problem,
they can be exploited for modular use.
But, we do not always understand the structure of information in our
problem domain.
Side note:
Understanding the structure of information in your problem domain is
important generally!
What if we allow evolving our encoding itself?
For example, to allow genes to switch positions?
Might functional gene assemblies move toward each other more over
evolutionary time?
Might functional gene assemblies move apart from each other less over
evolutionary time?
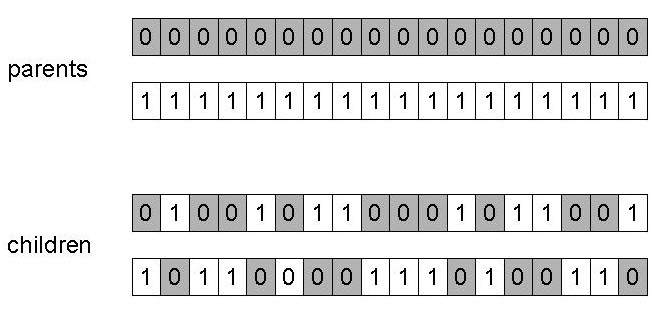
Choose n random, independent crossover points:
r1 = random(1, l-1)
r2 = random(1, l-1)
…
rn = random(1, l-1)
Split along those points.
Glue parts, alternating between parents.
Generalization of 1-point.
Still has some positional bias, but less.
This has both pros and cons,
depending on the mapping of the representation domain,
to the material problem domain.
Treat each gene independently,
and make a random choice as to which parent it should be inherited
from.
Uniform distribution over [0,1].
Assign ‘heads’ to one parent, ‘tails’ to the other.
Flip a coin for each gene of the first child.
Make an inverse copy of the gene for the second child.
Inheritance is independent of position.
When n-point is odd (e.g., one-point crossover),
there is a strong bias against keeping together certain combinations of
genes,
that are located at opposite ends of the representation.
These effects are known as positional bias.
This is extensively studied from both a theoretical and experimental
perspective.
This uniform method breaks ties between positions.
Uniform crossover does have a strong tendency towards transmitting 50%
of the genes from each parent,
and against transmitting an offspring with a large number of co-adapted
genes from one parent.
This is known as distributional bias.
We no longer capitalize on modularity to the same degree.
Which may or may not matter, depending on the encoding.
Discuss:
This is still better than pure mutation.
Why?
It is not usually easy state that one or the other of these operators
performs best on any given problem.
An understanding of the types of bias exhibited by different
recombination operators can be valuable,
when designing an algorithm for a particular problem,
particularly if there are known patterns or dependencies in the chosen
representation,
that can be exploited.
To use the knapsack problem as an example,
it might make sense to use an operator that is likely to keep together
the decisions for the first few heaviest items.
If the items are ordered by weight (cost) in our representation,
then we could make this more likely by using n-point crossover,
with its positional bias.
However, if we used a random weight ordering during knapsack
encoding,
then this might actually make it less likely that co-adapted values for
certain decisions were transmitted together,
so we might prefer uniform crossover.
Decade long debate:
which one is better / necessary / redundant?
Answer (at least, rather wide agreement):
it depends on the problem, but
in general, it is good to have both
Each have a different role.
Mutation-only-EA is possible.
Crossover-only-EA does not work with binary strings.
Why?
But, Crossover-only-EA may work with other representations.
A very general principle of learning agents under pressure.
There is co-operation AND competition between each.
Discovering promising areas in the search space,
i.e. gaining information on the problem.
To some extent, crossover is more exploratory,
as it makes a big jump to an area somewhere “in between” two
(parent) areas.
For binary strings, only mutation can introduce new information
(alleles).
For other representations, recombination can introduce new information
too.
Optimizing within a promising area, i.e. using information.
To some extent, mutation is more exploitative,
as it creates random small diversions,
thereby staying near (in the area of) the parent.
Only crossover can combine information from two parents.
For binary strings, crossover does not change the allele frequencies of
the population.
Thought experiment:
50% 0’s on first bit in the population,
?% after performing n crossovers.
Early on in the search process,
recombination makes rapid progress.
To hit the final optimum you often need a ‘lucky’ mutation.
Now it is generally accepted that it is better to encode
directly,
with numerical or discrete variables in the problem domain,
directly as numerical representations (integers, floating point
variables).
Many problems naturally have integer variables,
e.g. image processing parameters.
For integer problems,
we want to find the optimal values for a set of variables that all take
integer values.
These values might be either:
unrestricted
(i.e., any integer value is permissible),
Restricted to a finite set:
for example, if we are trying to evolve a path on a square grid,
we might restrict the values to the set {0,1,2,3}
representing {North, East, South, West}.
You could also consider this a string representation.
Would it matter?
How are strings encoded?
The representation is 1:1 (the same level of abstraction).
Strings can be considered a case of integer representation.
To decide whether to use an integer representation, we ask:
are there any natural relations between the possible values that an
attribute can take?
This might be obvious for ordinal attributes such as integers
(2 is more like 3 than it is 389),
But, for cardinal attributes such as the compass points above,
there may not be a natural ordering.
In either case an integer encoding is probably more suitable than a
binary encoding!
One example includes categorical values from a fixed set,
e.g. {blue, green, yellow, pink}
To give a well-known example of where there is no natural
ordering,
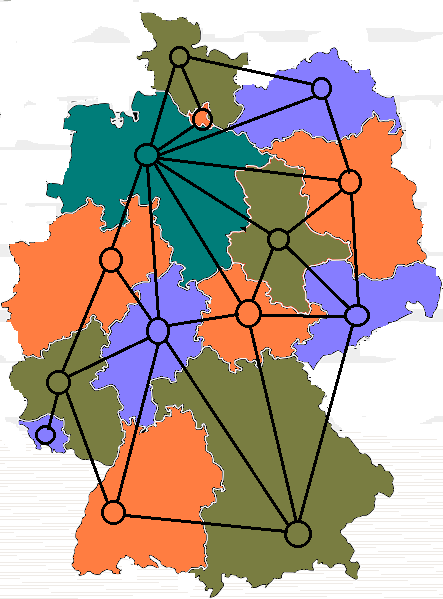
let us consider the graph k-coloring problem.
Here we are given a set of points (vertices),
and a list of connections between them (edges).
The task is to assign one of k colors to each vertex,
so that no two vertices, which are connected by an edge, share the same
color.
For this problem there is no natural ordering:
‘red’ is no more like ‘yellow’ than ‘blue’,
as long as they are different.
We could assign the colors, to the k integers representing them, in any
order,
and still get valid equivalent solutions.
For integer encodings, there are two principal forms of mutation used:
Random resetting
Creep mutation
Both mutate each gene independently,
with user-defined probability, pm
Here the logic of the bit-flipping mutation of binary
encodings,
is extended to create random resetting.
Preferable for many categorical variables
(of which strings are a case).
For example, random resetting is the most suitable operator to
use,
when the genes encode for cardinal attributes like direction,
or categorical values from a set like color.
This is because all other gene values are equally likely to be
chosen.
Rate, probability
In each position independently, with probability pm,
a new value is chosen at random from the set of permissible
values.
The probability distribution over fixed elements can be uniform, or not,
and is flexible.
This scheme was designed for ordinal attributes (where value, order
is meaningful).
Works by adding a small (positive or negative) value to each gene with
probability p.
Usually these values are sampled randomly for each position,
from a distribution that is symmetric about zero,
and is more likely to generate small changes than large ones.
Rate, probability
It should be noted that creep mutation requires a number of
parameters,
controlling the distribution from which the random numbers are
drawn,
and hence the size of the steps that mutation takes in the search
space.
Finding appropriate settings for these parameters may not be easy,
and it is sometimes common to use more than one mutation operator in
tandem from integer-based problems.
For example, both a “big creep” and a “little creep” operator are
sometimes used.
Alternatively, random resetting might be used with low
probability,
in conjunction with a creep operator that tended to make small
changes,
relative to the range of permissible values.
Just re-use the binary recombination
operations:
When each gene has a finite number of possible allele values, such as
integers,
it is normal to use the same set of operators as for binary
representations.
That’s easy!
These operators are valid:
The offspring can not fall outside the given genotype space.
These operators are also sufficient:
We usually want the discrete variables,
and it usually does not make sense to consider ‘blending’ allele
values.
For example, even if genes represent integer values,
averaging an even and an odd integer yields a non-integral result.
1-point

n-point

Uniform

Often the values that we want to represent as genes,
come from a continuous rather than a discrete distribution.
Many problems naturally occur as real valued problems.
For example, continuous parameter optimization,
where a gene might represent physical quantities such as:
the length, width, height, or weight,
of some component of a design,
that can be specified within a tolerance smaller than integer
values.
Satellite boom:
A good example would be the satellite dish holder boom described
earlier,
where the design is encoded as a series of angles and spar lengths.
Evolve weights in an ANN:
Another example might be if we wished to use an EA to evolve the weights
on the connections between the nodes in an artificial neural
network:
https://en.wikipedia.org/wiki/Neuroevolution
A vector (or string) of real values:
A string of real values can sensibly represent a solution to these
problems.
The genotype for a solution with k genes is now a vector:
\(<x_1,...,x_k> x_i \ with \in
\mathbb{R}\)
The precision of these real values is limited by the
implementation,
so clearly we operate using floating-point numbers in code.
Illustration: Ackley’s function (often used in EC)
https://en.wikipedia.org/wiki/Floating-point_arithmetic
How are floats encoded architecturally?
I’ll gloss over this in class:
\(Z \in [x,y] \subseteq \mathbb{R}\) is
represented by \(\{a_1, ..., a_L\} \in
\{0,1\}^L\)
\([x,y] \rightarrow \{0,1\}^L\) must be
invertible (one phenotype per genotype)
\(\Gamma: [x,y]^L \rightarrow [x,y]\)
defines the representation:
\(\Gamma (a_1, ...,a_L) = x + \frac{y-x}{2^L
-1} (\sum_{j=0}^{L-1}a_{L-j}) \in [x,y]\)
Only 2L values out of infinite are represented.
L determines possible maximum precision of solution.
But, note that:
High precision usually means slower computations.
We consider the allele values as coming from a continuous,
rather than a discrete, distribution.
Thus, the forms of mutation described above are no longer
applicable.
It is common to change the allele value of each gene randomly within
its domain given by a lower Li and upper Ui
bound:
\(<x_1, ..., x_n> \rightarrow
<x'_1, ..., x'_n>, where\ x_i,x'_i \in [L_i,
U_i]\)
We assume here that the domain of each variable is a single
interval:
\([L_i, U_i] \subseteq \mathbb{R}\)
Like integer representations,
two types can be distinguished by probability distribution,
from which the new gene values are drawn:
Analogous to bit-flipping (binary) or random resetting
(integers).
The values of x’i are drawn randomly with a uniform
distribution from [Li, Ui].
Like binary and integer, these are normally used with a position-wise
mutation probability, pm
Most schemes are probabilistic.
Usually only make a small change to each gene value.
Small adjustments
One common form is analogous to the creep mutation for integers.
Usually, but not always, the amount of change introduced is small.
Add to the current gene value,
an amount drawn randomly from a Gaussian distribution,
with mean zero and user-specified standard deviation.
\(N(0,\sigma)\) specifies a sample
from a normal distribution,
and paramaterizable standard deviation.
Updates as follows:
\(x'_i = x_i + N(0,\sigma)\)
then curtail the resulting value to the range [Li,
Ui] if necessary.
Size of adjustment
Standard deviation, \(\sigma\)
a.k.a, mutation step size, controls amount of change
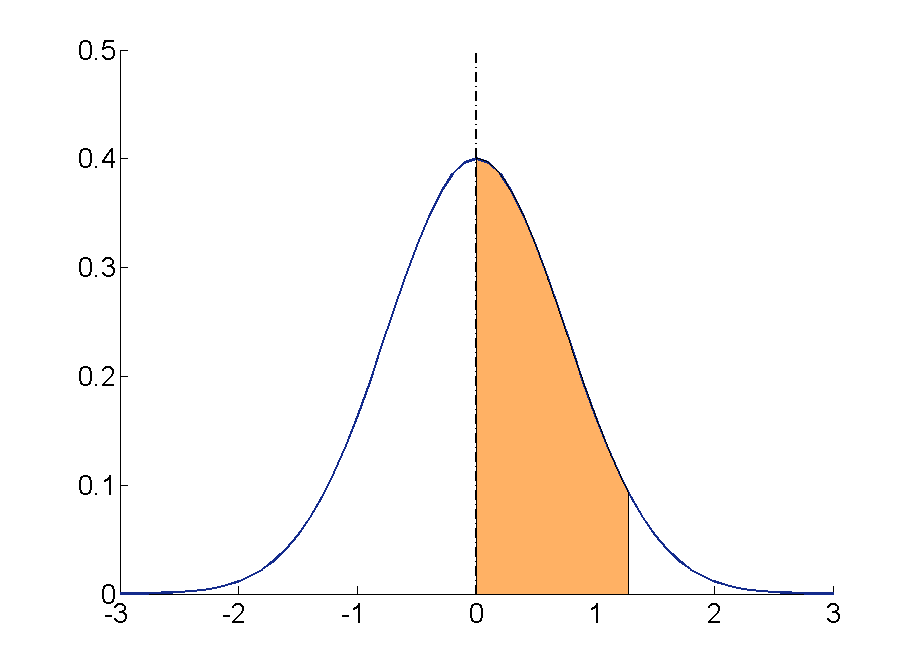
2/3 of draws will lie in range \((-\sigma \
to\ +\sigma)\)
With Gaussian, probability of drawing a random number,
with any given magnitude, is a rapidly decreasing from zero,
as a function of the standard deviation parameter, \(\sigma\)
Approximately two thirds of the samples drawn,
will lie within plus or minus one standard deviation.
So, most of the changes made will be small.
The tail of the distribution never reaches zero
So, there is nonzero probability of generating very large changes,
\(\sigma\) determines the extent to
which given values,
xi are perturbed by the mutation operator.
Thus, it is often called the mutation step size.
It is common to apply this operator with probability, 1 per gene,
pm=1.
Instead of infrequent application,
the mutation parameter is used to control the standard deviation of the
Gaussian,
and hence the probability distribution of the step sizes taken!
The Gaussian:
https://en.wikipedia.org/wiki/Normal_distribution
\(p(\Delta x_i)={\frac {1}{\sigma {\sqrt {2\pi
}}}}e^{-{\frac {1}{2}}\left({\frac {\Delta x_i-\epsilon }{\sigma
}}\right)^{2}} with\ \epsilon=0\)
Side note:
In general form, \(\epsilon\) would
normally be \(\mu\), the mean.
Here, it’s 0.
Different mutation strategies (rates),
may be appropriate in different stages of the evolutionary search
process,
or different parts of the landscape.
How to adapt step-sizes?
All representations:
As a side note, this self-adaptation sub-section is not just for
real/float,
or non-uniform floats, but for many types of representation.
This has been successfully demonstrated in many domains,
not only for real-valued representation,
but also for binary and integer search spaces.
Put step size in genome:
Mutation step sizes are not always set by the user.
\(\sigma\) can also be included in the
genome \(<x_1, ..., x_n,
\sigma>\)
Thus, step size can undergo variation and selection.
And, it can co-evolve with the solutions,
with all genes/alleles specified together as the vector, \(\bar{x}\)
Net mutation effect: \(<\bar{x}, \sigma> \rightarrow <\bar{x}', \sigma'>\)
Order of evaluation:
First modify the value of \(\sigma\)
\(\sigma \rightarrow \sigma'\)
Then, mutate each xi value with the new value \(\sigma'\)
\(x \rightarrow x' = x + N(0,
\sigma')\)
Thus, a new individual \(<\bar{x}',\sigma'>\) is effectively evaluated twice (a good thing).
First, it is evaluated directly for its viability,
during survivor selection based on \(f(\bar{x}')\)
If \(f(\bar{x}')\) is good, implies
\(\bar{x}'\) is good
Second, it is evaluated for its ability to create good
offspring.
If the \(\bar{x}'\) is good,
then this implies the new \(\sigma'\) that created it is good
If the offspring generated by using \(\bar{x}'\)
prove viable (in the first sense),
then a given step size that created it, evaluates favorably.
An individual \(<\bar{x}',\sigma'>\)
represents both a good \(\bar{x}'\)
that survived selection,
and a good \(\sigma'\) that proved
successful in generating this good \(\bar{x}'\) from \(\bar{x}\).
Assumptions
Assume that under different circumstances,
different step sizes will behave better than others.
Time and step size
Distinguish different stages within the evolutionary search
process,
and guess about the value of different mutation strategies,
which would be appropriate in different stages.
As the search is proceeding,
self-adaptation adjusts the mutation strategy.
Space and step size
The shape of the fitness landscape in its neighborhood,
determines what good mutations are.
Those that jump more into the direction of fitness, increase.
Assigning a separate mutation strategy to each individual,
which co-evolves with it,
opens the possibility to learn and use a better mutation operator,
suited for the local topology.
E.g., more caution on a steep hill, or speed on a flat section.
State of the art: self-adaptation works
Self-adaptive mutation mechanisms have been used,
and have been studied for decades in EC.
Experimental evidence shows that EA with self-adaptation,
outperforms the same algorithm without self-adaptation.
Theoretical results also show that self-adaptation works.
For simple objective functions,
theoretically optimal mutation step sizes can be calculated
in light of some performance criterion,
e.g., progress rate during a run,
and compared to step sizes obtained during a run of the EA in
question.
For complex problems and/or algorithms,
a theoretical analysis is usually infeasible.
Time-decay
For a successful run, the step size, \(\sigma\), often ideally decreases over
time.
Theoretical and experimental results agree on this observation.
In the beginning of a search process,
a large part of the search space has to be sampled in an exploratory
fashion,
to locate promising regions (with good fitness values).
Therefore, large mutations are appropriate in early phase.
As the search proceeds and optimal values are approached,
only fine tuning of the given individuals is needed
Smaller mutations are required during later search.
Landscape itself changes!
The objective function can change over a run!
This mean the landscape and fitness change.
The evolutionary process aims at a moving target.
Previously well-adapted individuals may now have a low fitness.
Population needs to be re-evaluated, and the search space
re-explored.
For the new exploration phase required,
late-stage mutation step sizes may be too low.
Implement an experimental test.
After each change in the objective function,
self-adaptation is able to reset the step sizes.
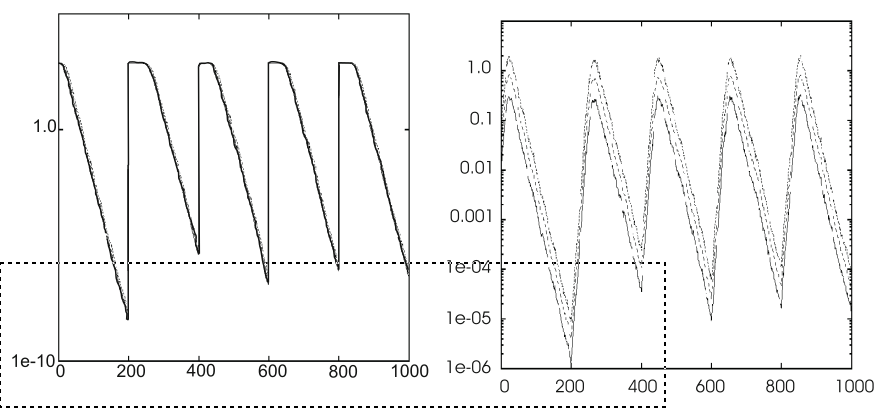
The optimum changes after every 200 generations (generations on
x-axes).
Clear effect on the average best objective function values,
(y-axis, left) in the given population.
Self-adaptation adjusts step sizes (y-axis, right).
We see a small delay to increase values,
appropriate for exploring the new fitness landscape, k
As the population approaches the new optimum,
the values of \(\sigma\) start
decreasing again.
Conclusions
Much experience has been gained over self-adaptation in Evolutionary
Algorithms.
The accumulated knowledge identifies helpful conditions for
self-adaptation.
With:
μ - population size
λ - number of offspring
Back to mutation for to float representations:
Chromosome
\(<x_1, ..., x_n, \sigma>\)
The same distribution, \(\sigma\),
is used to mutate each xi
One strategy parameter \(\sigma\) in
each individual.
\(\sigma\) is mutated, each time
step.
Multiply it by a term \(e^\Gamma\),
where \(\Gamma\) is a random variable
drawn each time,
from a normal distribution with mean 0 and standard deviation \(\tau\).
N(0, 1) denotes a draw from the standard normal distribution
(with stardard deviation 1 instead of parameterizable \(\sigma\)).
Ni(0, 1) denotes a separate draw from the standard normal
distribution,
for each variable i .
The proportionality constant \(\tau\) is an external parameter, to be set
by the user.
\(N(0, \tau) = \tau \cdot N(0,1)\)
The mutation mechanism for \(\sigma\)
\(\sigma' = \sigma \cdot e^{\tau \cdot
N(0,1)}\)
The mutation mechanism, for each x
\(x'_i = x_i + \sigma' \cdot
N_i(0,1)\)
The parameter \(\tau\) can be
interpreted as a kind of learning rate,
as in neural networks.
It is usually inversely proportional to the square root of the problem
size.
\(\tau \propto 1/\sqrt{n}\)
Why mutate with distribution?
The reasons for mutating \(\sigma\) by
multiplying with a variable with a lognormal distribution as
follows:
Smaller modifications should occur more often than large ones.
Standard deviations have to be greater than 0.
The median (0.5-quantile) should be 1, since we want to multiply the
\(\sigma\).
Mutation should be neutral on average.
This requires equal likelihood of drawing a certain value,
and its reciprocal value, for all values.
Lower limit
Standard deviations very close to zero are unwanted.
They will have on average a negligible effect.
The following boundary rule is used to force step sizes to be no smaller
than a threshold:
\(\sigma' < \epsilon_0 \Rightarrow
\sigma' = \epsilon_0\)
If less than limit, then set to limit.
Example effect on landscape (image)
We have an objective function, \(\mathbb{R}^2
\rightarrow \mathbb{R}\).
Individuals in this example are of the form \(<x, y, \sigma>\).
The mutation step size is the same in each direction.
There are limited points in the search space where new offspring can be
placed.
Such placement is drawn as a circle around the individual to be
mutated.
The image below shows the effects of mutation in two dimensions.
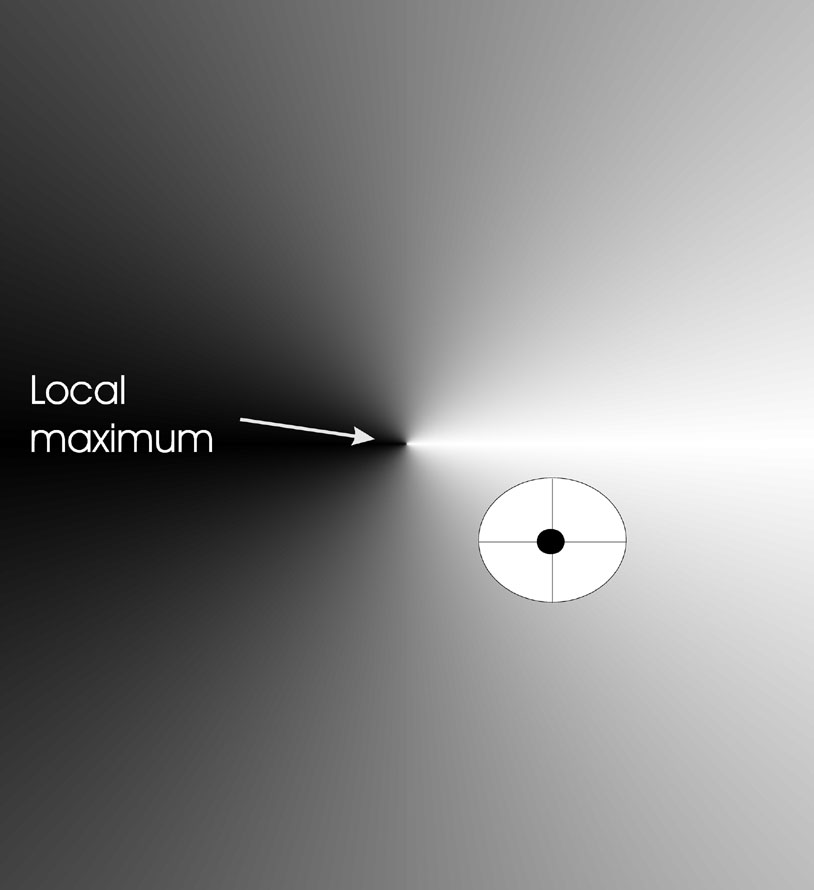
Part of a fitness landscape with a conical shape is shown.
The black dot indicates an individual.
Circle is mutants having the same chance to be created.
Mutation with n = 2, \(n_\sigma\) = 1,
\(n_\alpha\) = 0 (angle, more on alpha
later).
There is just one \(\sigma\).
Thus, the probability of moving along the y-axis (little effect on
fitness),
is the same as that of moving along the x-axis (large effect on
fitness)
Use n step sizes to treat each dimension (gene) differently.
Use different step sizes for different dimensions:
\(i \in \{1, ..., n\}\)
The fitness landscape can have a different slope in one direction
(along axis i),
than in another direction (along axis j).
Each basic chromosome:
\(<x_1, ..., x_n>\)
Extend with n step sizes, one for each dimension, resulting in:
\(<x_1, ..., x_n, \sigma_1, ...,
\sigma_n>\)
The step size mutation mechanism:
\(\sigma'_i = \sigma_i \cdot e^{\tau'
\cdot N(0,1) + \tau \cdot N_i(0,1)}\)
The x mutation mechanism:
\(x'_i = x_i + \sigma'_i \cdot
N_i(0,1)\)
where:
\(\tau' \propto 1/2n\)
\(\tau' \propto 1
\sqrt{2\sqrt{n}}\)
A boundary rule is applied to prevent standard deviations very close
to zero:
\(\sigma' < \epsilon_0 \Rightarrow
\sigma' = \epsilon_0\)
Instead of the individual level (each individual \(\bar{x}\) having its own \(\sigma\)),
it works on the coordinate level (one \(\sigma_i\) for each xi in \(\bar{x}\)).
The corresponding straightforward modification could be:
\(\sigma'_i = \sigma_i \cdot e^{\tau \cdot
N_i(0,1)}\)
Though we use the more complicated one above, for multiple \(\tau\).
The common base mutation \(e^{\tau'
\cdot N(0,1)}\) allows for an overall change of the
mutability,
guaranteeing the preservation of all degrees of freedom.
The coordinate-specific \(e^{\tau'
\cdot N_i(0,1)}\) provides flexibility,
to use different mutation strategies in different directions.
Effect on landscape
The image below shows the effects of mutation in two dimensions.
We have an objective function \(\mathbb{R}^2
\rightarrow \mathbb{R}\).
The black dot indicates an individual.
Individuals are of the form \(<x,y,\sigma_x, \sigma_y>\).
Mutation step sizes can differ in each direction (x and y).
The points in the search space where the offspring can be placed,
with a given probability,
form an ellipse around the individual to be mutated.
The axes of such an ellipse are parallel to the coordinate axes,
with the length along axis i proportional to the value of \(\sigma_i\)
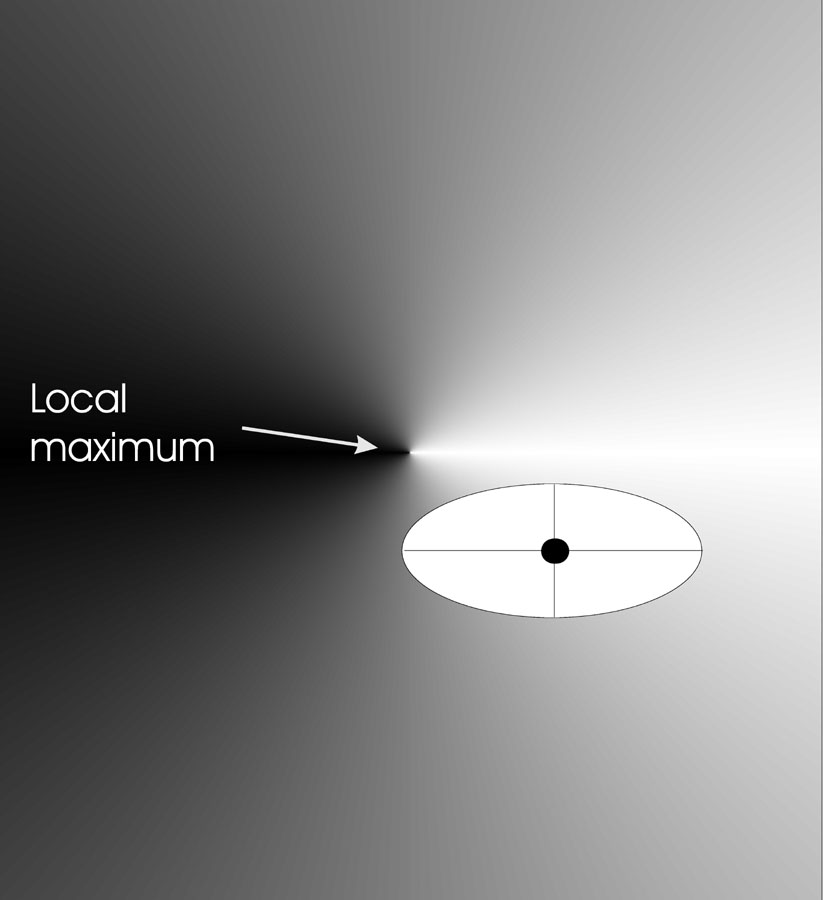
The second version of mutation discussed above,
introduced different standard deviations for each axis,
but this only allows ellipses orthogonal to the axes.
The rationale behind correlated mutations,
is to allow the ellipses to have any orientation,
by rotating them with a rotation (covariance) matrix C.
Comparing our previous two strategies to correlated mutations:

Possible settings of \(n_{\sigma}\)
(step) and \(n_{\alpha}\)
(angle),
for previous two mutation operators (row 1, 2),
and correlated on row 3.
The image below shows the effects of correlated mutations in two
dimensions:
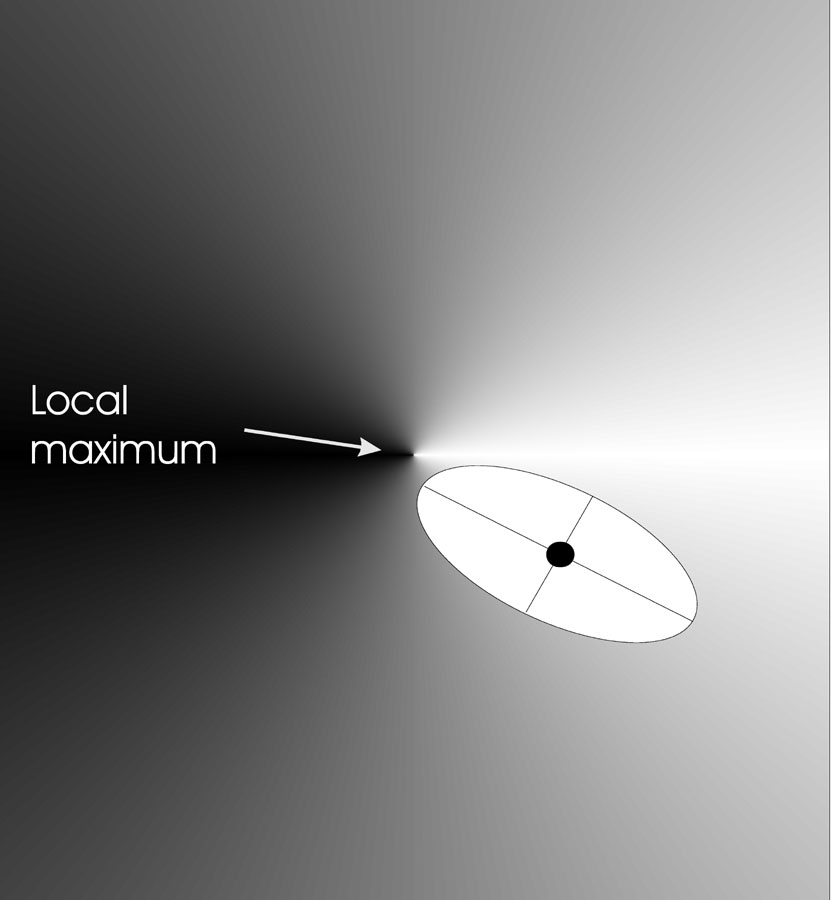
Correlated mutation: n = 2, \(n_{\sigma}\) = 2 (step), \(n_{\alpha}\) = 1 (angle).
The black dot indicates an individual.
The individuals now have the form
\(<x, y, \sigma_x, \sigma_y,
\alpha_{x,y}>\)
The points in the search space where the offspring can be placed,
with a given probability,
form a rotated ellipse around the individual to be mutated,
where again the axis lengths are proportional to the \(\sigma\) values.
Points where the offspring can be placed,
with a given probability,
form a rotated ellipse.
The probability of generating a move in the direction of the steepest
ascent
(largest effect on fitness) is now larger than that for other
directions.
Three major categories for floats:
1. Discrete
2. Intermediate / Arithmetic
3. Blend
Analogous operator to those used for bit-strings,
but now split between floats.
Recombination only gives us new combinations of existing values.
If discrete recombination is used,
then only mutation can insert new values into the population.
This is true of all of the recombination operators described
previously.
Each allele value in offspring z,
comes from one of its parents (x, y),
with equal probability:
zi = xi or
yi
Create a new allele value in the offspring,
that lies between those of the parents.
\(z_i = \alpha x_i + (1 - \alpha) y_i \ where
\ \alpha: 0 \leq \alpha \leq 1\)
The parameter \(\alpha\) can be
either:
constant, uniform arithmetical crossover,
variable, (e.g. depend on the age of the
population),
random, every time.
\(\alpha\) serves as a weight between
the two parents,
that auto-adjusts to 1.
This form of recombination creates new gene material.
However, as a result of the averaging process,
the range of the allele values in the population for each gene is
reduced.
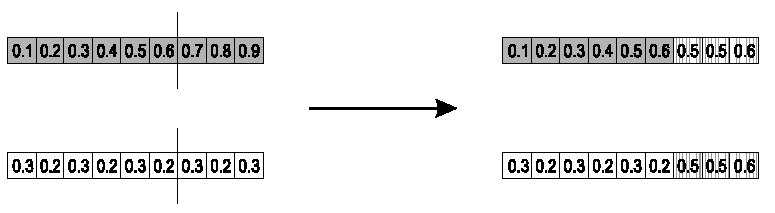
Parents:
\(<x_1, ..., x_n> and \ <y_1, ...,
y_n>\)
Pick a single gene (k) at random.
At that position, k,
take the arithmetic average of the two parents.
The other points are copied from the parents.
Child 1:
\(<x_1, ..., x_{k - 1}, \alpha \cdot y_k +
(1 - \alpha) \cdot x_k, x_{k + 1}, ..., x_n>\)
Child 2:
The second child is created in the same way,
with x and y reversed.
e.g., k = 8, α = 1/2

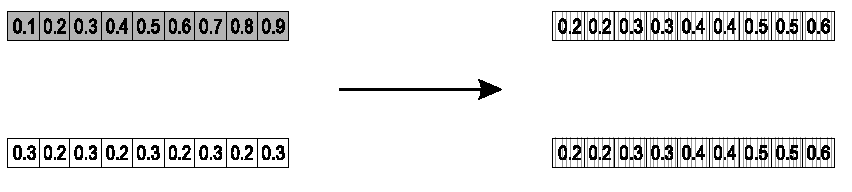
Parents:
\(<x_1, ..., x_n> and \ <y_1, ...,
y_n>\)
First pick a recombination point k, after which, mean all values.
Take the first k floats of parents, and put them into the
children.
The rest is the arithmetic average of parent 1 and 2.
Child 1:
\(<x_1, ..., x_k, \alpha \cdot y_{k + 1} +
(1 - \alpha) \cdot x_{k + 1}, ..., \alpha \cdot y_n + (1 - \alpha) \cdot
x_n>\)
Child 2:
The second child is created in the same way,
with x and y reversed.
e.g., with \(\alpha\) = 0.5, k =
6
This is the most commonly used operator.
Parents:
\(<x_1, ..., x_n> and \ <y_1, ...,
y_n>\)
For each gene, take the weighted sum of the two parental alleles.
Child 1 is:
\(\alpha \cdot \bar{x} + (1 - \alpha) \cdot
\bar{y}\)
Child 2 is revers:
\(\alpha \cdot \bar{y} + (1 - \alpha) \cdot
\bar{x}\)
e.g., with α = 1/2
Create a new allele value in the offspring,
which is close to that of one of the parents,
but may lie outside them.
Child value could be bigger than the larger of the two parent
values,
or smaller than the lesser parent.
Can create new material,
without restricting the range.
Create offspring in a region that is bigger,
beyond the n-dimensional rectangle spanned by the parents.
Extra space is often proportional to the distance between the
parents.
Parents that are farther apart yields more outer range.
Two parents x and y:
\(<x_1, ..., x_n> and \ <y_1, ...,
y_n>\)
For example, in chromosome position i, some value xi <
yi
The difference is:
di = yi - xi
To create a child we can sample a random number u uniformly from [0,
1], calculate:
\(\gamma = (1 - 2\alpha)\mu -
\alpha\)
and set:
\(z_i = (1 - \gamma) x_i + \gamma
y_i\)
Range for the ith value in the child z is \(z_i = [x_i - \alpha d_i, x_i + \alpha
d_i]\)
Interestingly, the original authors reported best results with \(\alpha = 0.5\).
where the chosen values are equally likely to lie inside the two parent
values, as outside.
This may balance exploration and exploitation.
Difference between:
single arithmetic recombination,
whole arithmetic combination, and
Blend Crossover.
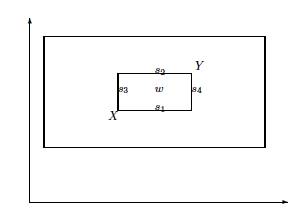
X and Y are individuals (the corners).
Single:
The points {s1, … , s~4} are four possible offspring,
from single arithmetic recombination with \(\alpha = 0.5\).
Whole:
The single point, w,
is the offspring from whole arithmetic recombination with \(\alpha = 0.5\).
Inner box represents all the possible offspring positions,
as \(\alpha\) is varied.
Blend:
The outer dashed box shows all possible offspring positions,
for blend crossover with \(\alpha =
0.5\),
each position being equally likely.
More recent methods, such as Simulated Binary Crossover,
have built on Blend Crossover,
so that rather than select offspring values uniformly,
from a range around each parent values,
select from a distribution more likely to create small changes,
and the distribution is controlled by the distance between the
parents.
We are not constricted by the conservative practicalities of
nature!
Mutation uses n = 1 parent.
Traditional crossover n = 2.
Extension to n > 2 is natural to examine.
Been around since 1960s (Prehaps a product of the times, lol…).
Still rare, but studies indicate sometimes useful.
Type 1
Type 2
Many problems decide on the order of a sequence of events.
Representations define a permutation of a fixed set of values.
Fixed values are typically integers.
A binary, or simple integer, representation allows numbers to occur
more than once.
Such sequences of potentially repeating integers would not represent
valid permutations.
Mutation and recombination operators must preserve the unique
permutation property.
Each possible allele value must occur exactly once in the solution.
decoder functions based on unrestricted integer
representations,
“floating keys” based on real-valued representations,
etc.
Represent each candidate solution as a list of integers.
Each queen was on a different column, or list position.
Each integer value represented the rows on which a queen was
positioned.
We required that these be a permutation of unique elements.
Thus, no two queens can share the same row.
Two classes of permutation problem exist:
order, and
adjacency.
Absolute order can determine correctness.
This might happen when the events use limited resources or time.
A typical example is the production scheduling problem.
In which order should a series of products be manufactured on a set of
machines?
There may be dependencies between products.
Specifically, there might be different setup times between
products.
Further, one product might be a component of another.
For example, it might be better for widget 1 to be produced before
widgets 2 and 3,
which in turn might be preferably produced before widget 4,
no matter how far in advance this is done.
In this case it might well be that the sequences [1,2,3,4] and [1,3,2,4]
have similar fitness,
and are much better than, for example, [4,3,2,1].
Adjacency can define correctness.
A common example is the:
https://en.wikipedia.org/wiki/Travelling_salesman_problem
How do we find a complete tour of n cities, of minimal length?
There are (n-1)! different routes possible, for n given cities.
This includes the asymmetric case, counting back and forth as two
routes…
For n = 30 there are approximately 1032 different
tours.
We label the cities 1, 2, …, n.
A complete tour is defined by a permutation.
It is the links between cities that are important.
The difference from absolute ordering problems is subtle.
Starting point of a tour is not important.
For example, [1,2,3,4], [2,3,4,1], [3,4,1,2], and [4,1,2,3] are all
equivalent.
As we mentioned before, many examples of this class are also
symmetric.
To extend the example, [4,3,2,1] is also equivalent.
Two possible methods to encode a permutation exist.
We can use an example of four cities:
[A,B,C,D].
A represented permutation, or candidate solution, could be:
[3,1,2,4].
In the first method,
the ith element of the representation denotes the event that
happens,
in that place in the sequence.
(TSP: the ith destination visited).
The first encoding denotes one tour of [A,B,C,D] as:
[3,1,2,4] as [C,A,B,D]
In the second method,
the value of the ith element denotes the position in the
sequence,
in which the ith event happens.
The second encoding denotes one tour of [A,B,C,D] as:
[3,1,2,4] as [B,C,A,D].
Discussion question:
Which method do you find most intuitive?
Do you have any idea why?
Mutate one permutation to produce another valid permutation.
Independence
For previous representations, we defined an independent probability that
a single gene in the chromosome is altered.
It is longer possible to consider each gene independently.
Now, finding legal mutations requires moving alleles around in the
genome.
The mutation parameter is interpreted as the probability that the
chromosome undergoes mutation.
Uniqueness
Previously covered mutation operators can lead to inadmissible solutions
for permutations.
For example, let gene i have value j.
If we change j to some other value k,
then k would occurr twice,
and j would no longer occur.
We review four methods of mutation for permutation:
Swap,
Insert,
Scramble, and
Inversion.
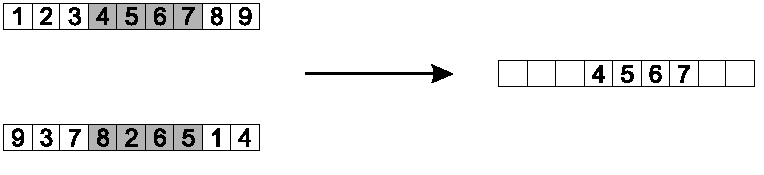
Randomly select two positions (genes) in the chromosome.
Swap allele values.
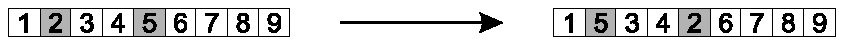
Image: Positions 2 and 5 were chosen, and swapped.
Randomly select two gene positions (allele values).
Shift the second forward, to immediately follow the first.
Shift those between later, to accommodate.
This preserves most of the order, and much adjacency information.
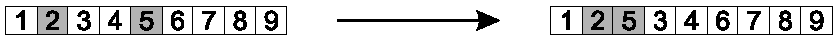
Image: Positions 2 and 5 were chosen, and 5 shifted backward.
Randomly select a contiguous range of genes.
Randomly re-arrange the alleles in those positions.
If range is large enough, in the limit, this scramble the entire
chromosome.

Image: Positions 2-5 were chosen, and randomly permuted.
The first three operators make small changes,
to the order in which allele values occur.
For adjacency-based problems,
this can cause large numbers of links to be broken.
Thus, for adjacency problems, inversion is commonly used.
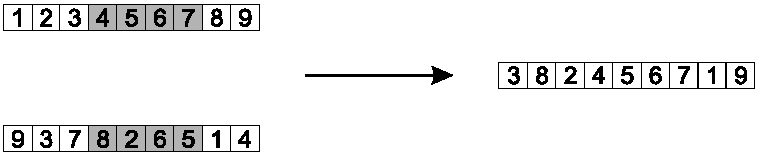
Inversion reverses a randomly chosen sub-string.
Steps:
Randomly select two positions in the chromosome.
Choosing two positions breaks the chromosome into three parts.
In the middle part, reverse the order in which the values appear.
All links inside each part are preserved.
The two links between the three parts are broken.
This operator is illustrated here:
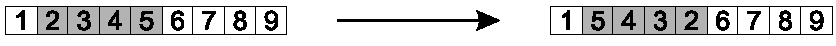
Image: positions 2-5 were selected, and inverted.
Generalization:
At a range of 2 genes, inversion is the smallest change,
that can be made to an adjacency-based problem.
All other types of changes could be constructed as a series of
inversions.
Ordering of the search space induced by this operator,
forms a natural basis for considering this class of problems as a
whole.
It is similar to the Hamming space for binary problem
representations.
It is also the basic logic behind the 2-opt search heuristic for
TSP,
and by extension k-opt:
https://en.wikipedia.org/wiki/2-opt
++++++++++++++ Cahoot 04-n
Combine 2+ permutation parents,
to produce valid permutation offspring.
For the design of recombination operators,
permutation-based representations present some difficulties.
It is not generally possible simply to exchange sub-strings between
parents,
and still maintain the unique permutation property.
What do the solutions actually represent?
an order in which elements occur, or
a set of transitions linking pairs of elements.
Specialized recombination operators must be designed for
permutations.
Operators ideally transmit information contained in the parents.
Some emphasize transmitting information in either parent.
Some emphasize transmitting information shared between parents.
Now, we will review the following methods:
Partially mapped crossover (PMX),
Edge recombination,
Order recombination, and
Cycle recombination.
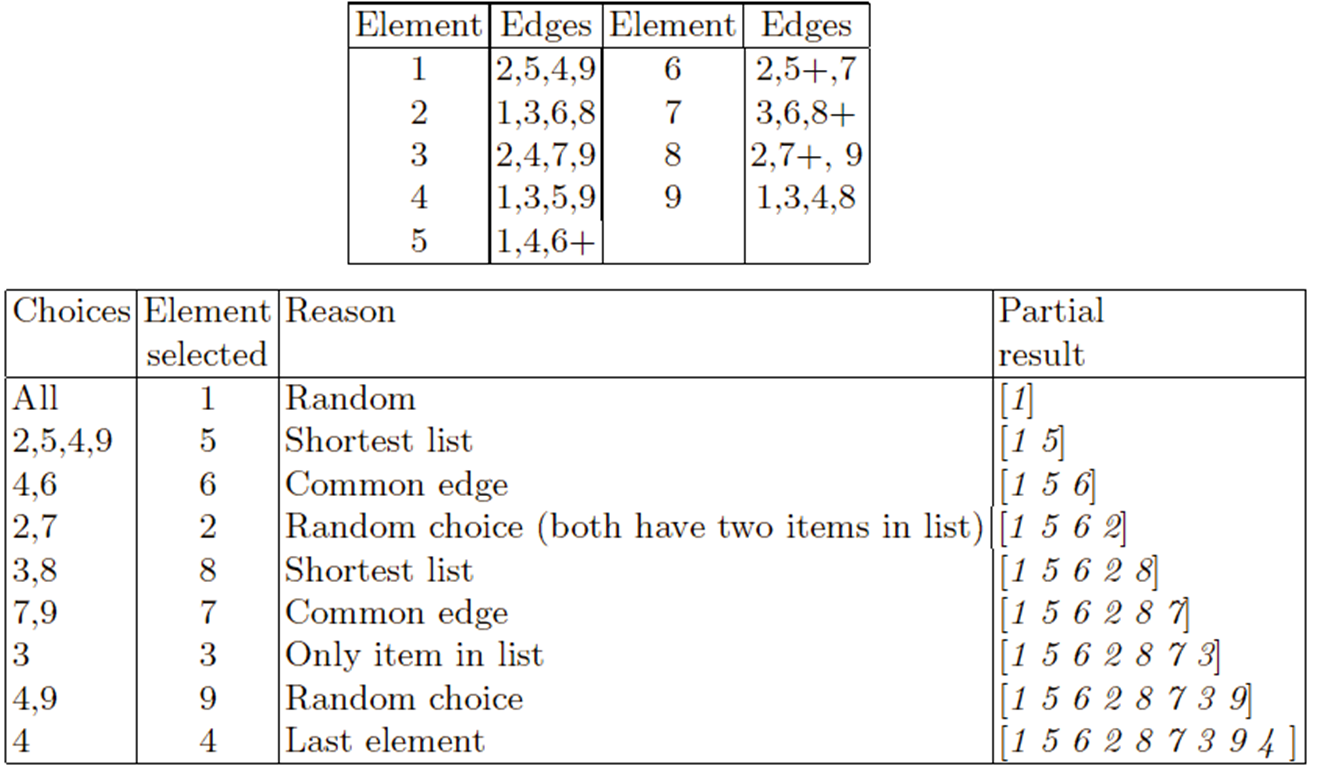
Procedure for parents P1 and P2:
Choose two crossover points at random.
Copy the segment between them from the first parent (P1) into the first
offspring.
Starting from the first crossover point,
look for elements in that segment of the second parent (P2),
that have not been copied.
For each of these (say i),
look in the offspring to see what element (say j),
has been copied in its place from P1.
Place i into the position occupied by j in P2,
since we know that we will not be putting j there
(as we already have it in our string).
If the place occupied by j in P2,
has already been filled in the offspring by an element k,
then put i in the position occupied by k in P2.
Having dealt with the elements from the crossover segment,
the remaining positions in this offspring can be filled from P2.
The second child is created analogously with the parental roles
reversed.
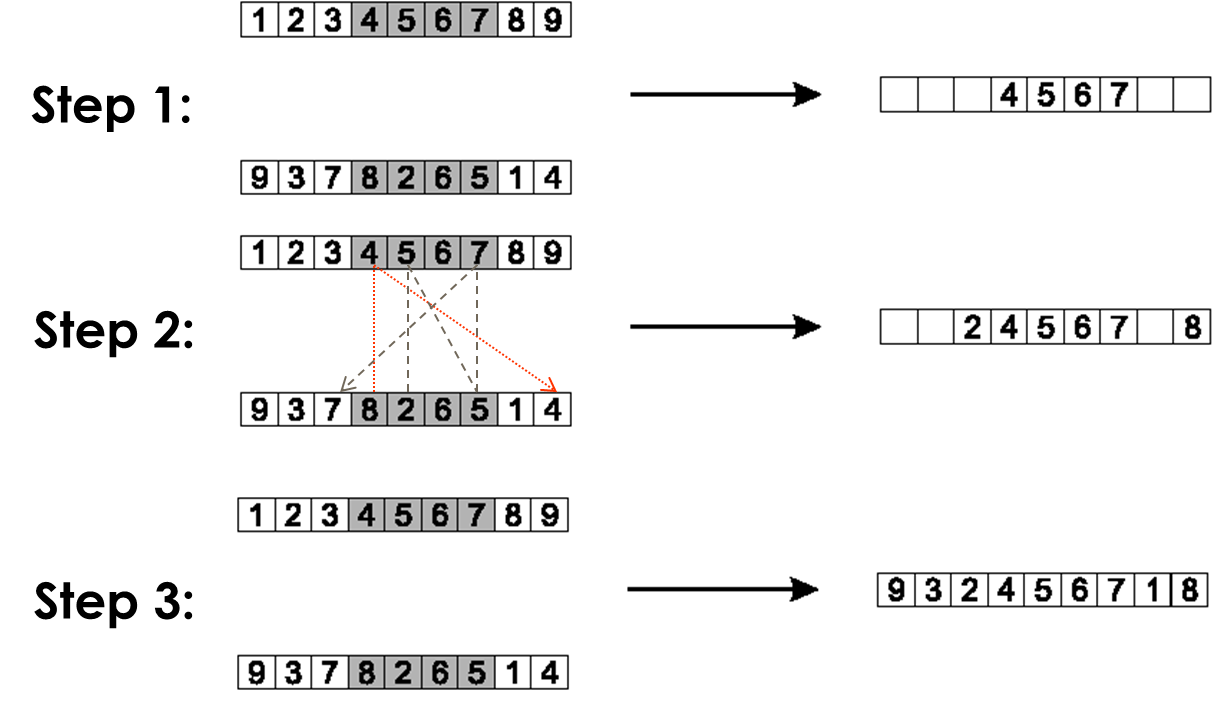
step 1:
copy randomly selected segment from first parent into offspring.
step 2:
consider in turn the placement of the elements that occur in the middle
segment of parent 2 but not parent 1.
The position that 8 takes in P2 is occupied by 4 in the offspring,
so we can put the 8 into the position vacated by the 4 in P2.
The position of the 2 in P2 is occupied by the 5 in the offspring,
so we look first to the place occupied by the 5 in P2, which is position
7.
This is already occupied by the value 7,
so we look to where this occurs in P2,
and finally find a slot in the offspring that is vacant, the
third.
Finally, note that the values 6 and 5 occur in the middle segments of
both parents.
step 3:
copy remaining elements from second parent into same positions in
offspring
Preserve what parents share?
Inspection of the offspring created shows that in this case,
six of the nine links present in the offspring,
are present in one or more of the parents.
However, of the two edges {5-6} and {7-8} common to both parents,
only the first is present in the offspring.
Some suggest that a desirable property of any recombination operator is
that of parental respect,
i.e., that any information carried in both parents should also be
present in the offspring.
This is true for all of the recombination operators described above for
binary and integer representations,
and for discrete recombination for floating-point representations,
However, as the example above shows, is not necessarily true of
PMX.
Several other operators have been designed for adjacency-based
permutation problems:
Offspring are be created such that its edges are present in at lest
one of the parents.
Edge recombination has undergone a number of revisions over the
years.
Here we show a design that ensures common edges are preserved.
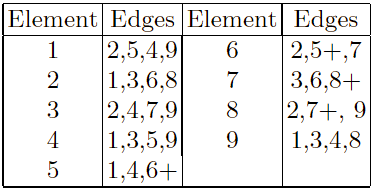
Using the two parents, an edge table is constructed.
This edge table is also known as an adjacency list.
For each element, it lists the other elements that are linked to it, in
the two parents.
Marking a ‘+’ in the table indicates that an edge is present in both
parents.
The operator works as follows:
Construct a table listing which edges are present in the two
parents.
If an edge is common to both, mark it with a +.
For example, parents:
[1 2 3 4 5 6 7 8 9] and [9 3 7 8 2 6 5 1 4]
Start randomly.
Pick an initial element, entry, at random, and put it in
the offspring.
Set a variable, current_element=entry.
Remove all references to current_element from the
table.
Examine edge list for current_element.
If there is a common edge (+),
then pick that to be next element.
If not,
then pick the entry in the list which itself has the shortest
list.
Split ties at random.
In the case of reaching an empty list,
the other end of the offspring is examined for extension.
Otherwise, a new element is chosen at random.
Only in the last case, will so-called foreign edges be introduced.
Edge-3 recombination is illustrated by the following example.
The parents are the same two permutations used in the PMX example:
[ 1 2 3 4 5 6 7 8 9] and [ 9 3 7 8 2 6 5 1 4].
Note that only one child per recombination is created by this
operator.
This operator begins in a similar fashion to PMX.
It copies a randomly chosen segment of the first parent into the
offspring.
However, it proceeds differently.
The intention is to transmit information about relative order from the
second parent.
Next, choose two crossover points at random.
Copy the segment between them from the first parent (P1) into the first
offspring.
Starting from the second crossover point in the second parent,
copy the remaining unused numbers into the first child,
in the order that they appear in the second parent,
wrapping around at the end of the list.
Create the second offspring in an analogous manner, with the parent
roles reversed.
Copy randomly selected set from first parent:
Copy the rest from second parent, in order 1,9,3,8,2
Summary
Preserves as much information as possible about the absolute position
in which elements occur.
A cycle is a subset of elements that has the following property:
Each element always occurs paired with another element of the
same cycle when the two parents are aligned.
Notice the three example cycles below.
Then, re-read that definition above.
Divide the elements into cycles.
Select alternate cycles from each parent, to create offspring.
The procedure for constructing cycles is as follows:
1. Start with the first unused position and allele of P1.
2. Look at the allele in the same position in P2.
3. Go to the position with the same allele in P1.
4. Add this allele to the cycle.
5. Repeat steps 2 through 4 until you arrive at the first allele of
P1.
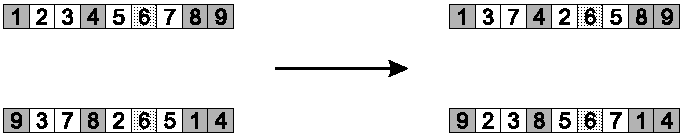
Step 1: identify cycles

Three cycles were identified.
Step 2: copy alternate cycles into offspring
Summary
Trees are a universal form.
They represent varied objects in computing.
In general, parse trees capture expressions in a given formal
syntax.
A tree might represent:
the syntax of arithmetic expressions,
formulas in first-order predicate logic, or
code written in a programming language.
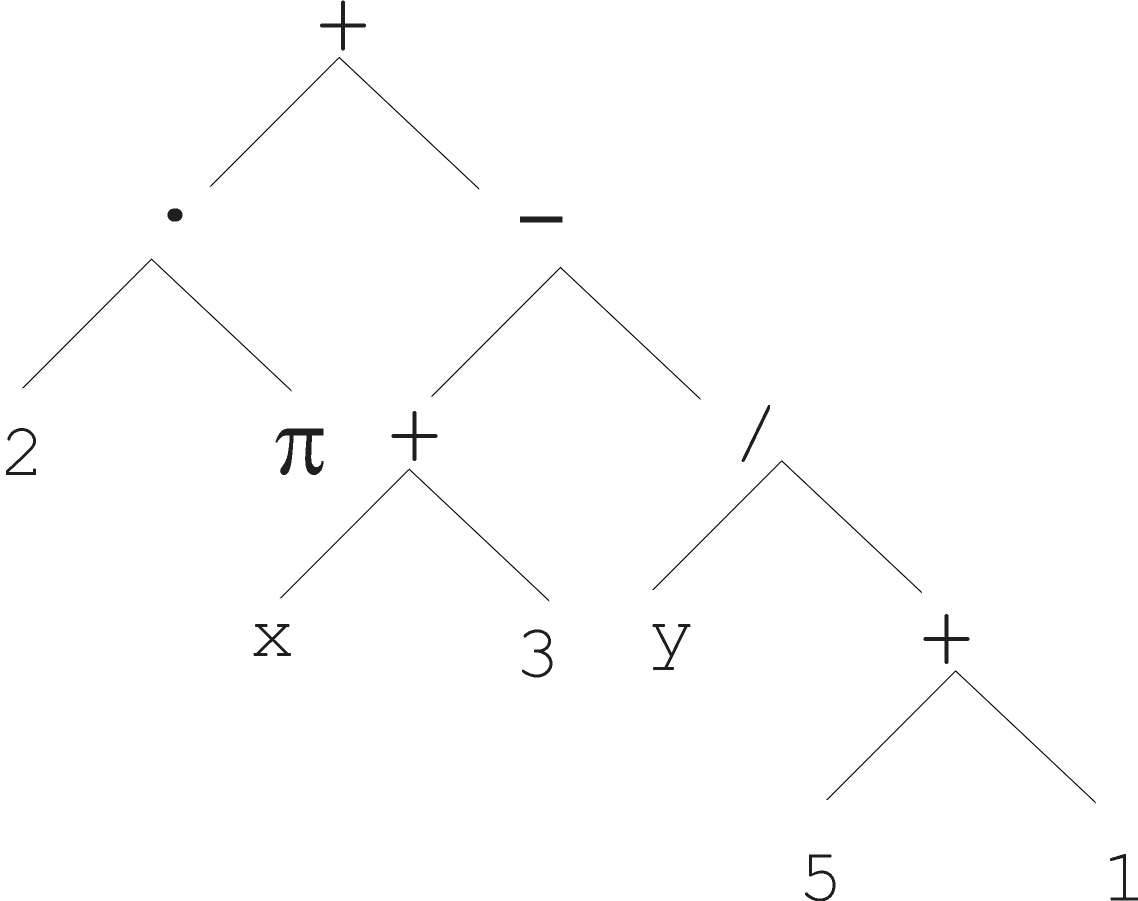
Arithmetic formula:
\(2 \cdot \pi + ((x + 3) -
\frac{y}{5+1})\)
And it’s abstract tree:
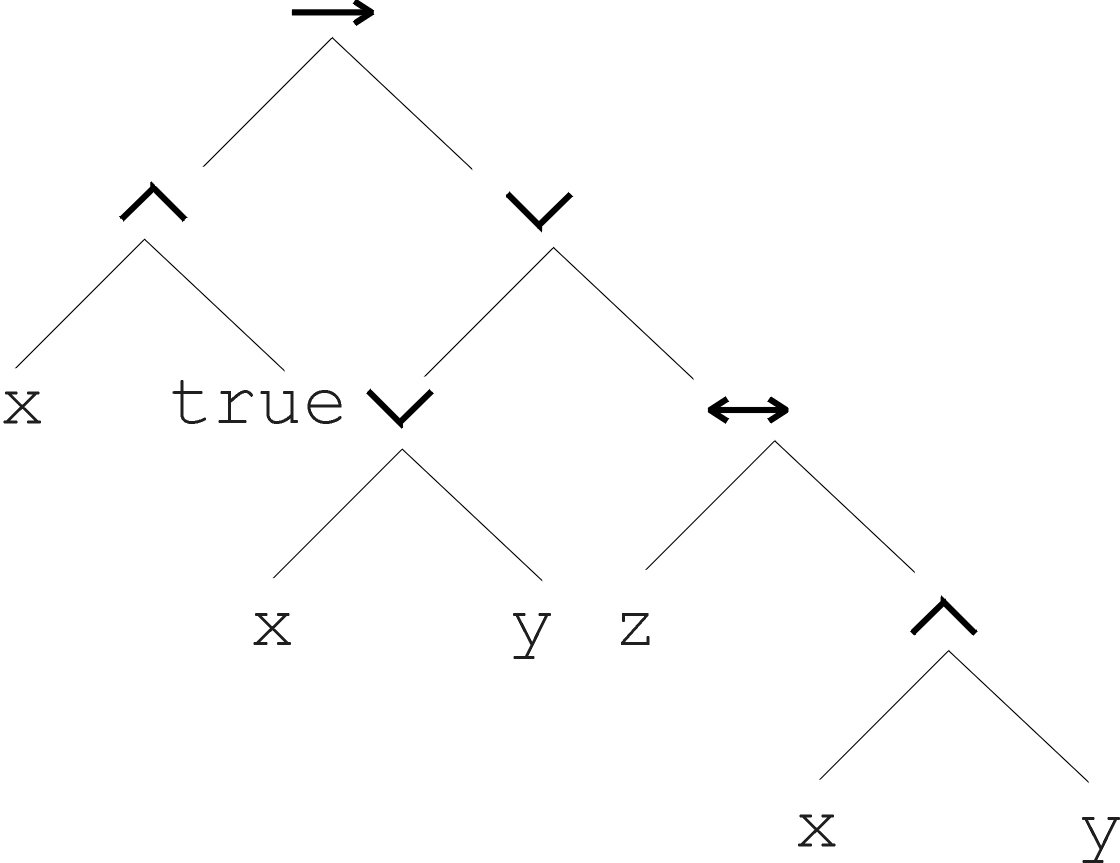
Logical formula:
\((x \land true) \rightarrow ((x \lor y) \lor
(z \leftrightarrow (x \land y)))\)
And it’s abstract tree:
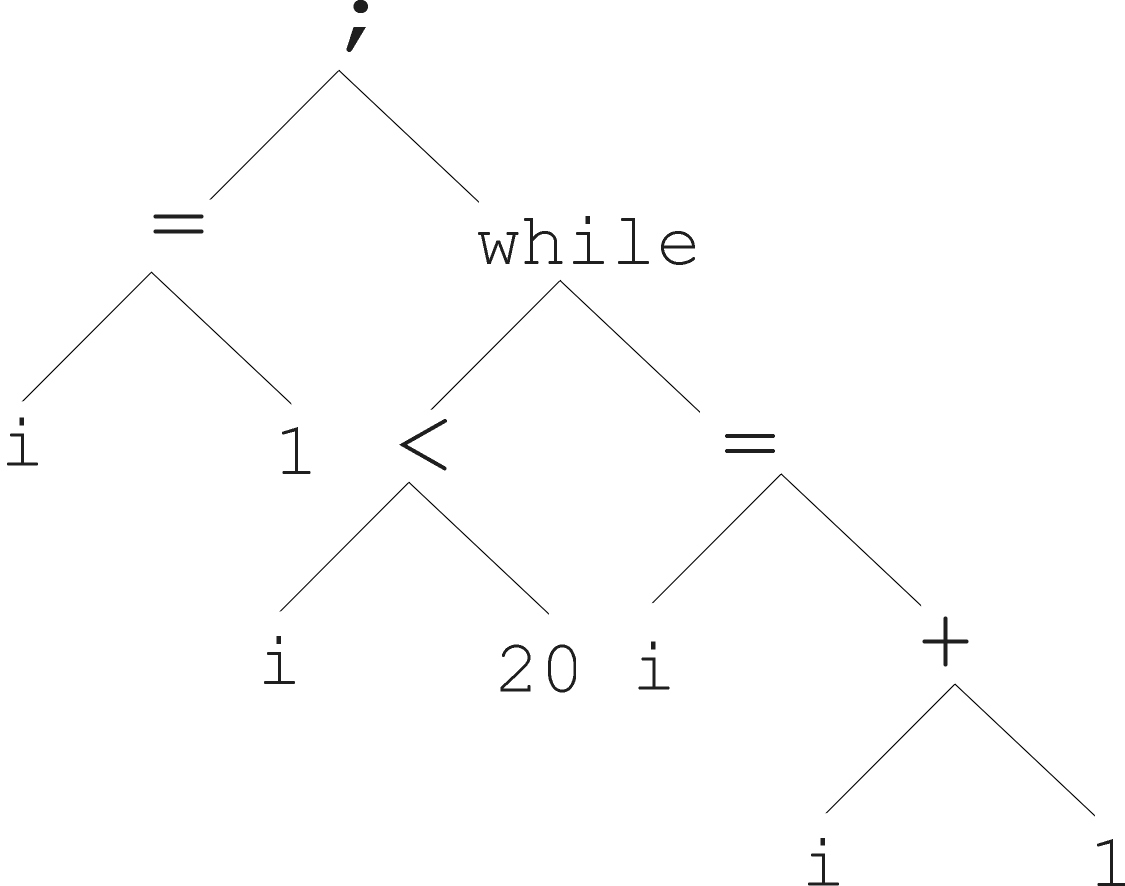
Program:
And it’s abstract tree:
Genetic programming (GP) employs tree representations.
These representations require different methods than before.
In GA, ES, and EP, chromosomes are linear structures.
These included bit strings, integer string, real-valued vectors,
permutations, etc.
Tree chromosomes in GP are non-linear structures.
In GA, ES, and EP, the size of the chromosomes is fixed.
These included various strings of equal length.
Tree chromosomes in GP may vary in depth and width.
Representing individuals involves defining the syntax of the
trees.
The syntax of the symbolic expressions (s-expressions) represents
trees.
Defining a function set and a terminal set.
Allow elements of the terminal set as leaves.
Allow symbols from the function set as internal nodes.
For example:
\(2 \cdot \pi + ((x + 3) -
\frac{y}{5+1})\)

Function set {+, −, ·, /}
Terminal set IR ∪ {x, y}
Two general parts are often omitted:
1. Specify the arity for each function in the set.
2. Define correct expressions (trees) on the function and terminal
set.
Those parts follow now:
All elements of the terminal set T are correct expressions.
If \(f \in F\) is a function
symbol,
with arity n,
and if each of \(e_1, ..., e_n\) is a
correct expression, then so is \(f(e_1, ...,
e_n)\).
There are no other forms of correct expressions.
To summarize:
Every \(t \in T\) is a correct
expression.
If the following are correct expressions:
\(f \in F\),
\(arity(f)=n\), and
\(e_1, ..., e_n\)
then, \(f(e_1, ..., e_n)\) is a correct
expression.
There are no other forms of correct expressions.
In the original standard GP, expressions are not typed.
In the above definition, we do not distinguish different types of
expressions.
Each function symbol in the example can take any expression as
argument.
This feature is known as the closure property.
Formally, any \(f \in F\) can take any
\(g \in F\) as an argument.
In practice, function symbols and terminal symbols are often
typed.
Typed symbols impose extra syntactic requirements.
A problem might require both arithmetic and logical function
symbols.
For example, typing enables (N = 2) ∧ (S > 80.000)) as a correct
expression.
In this latter example, it is necessary to enforce another rule:
Arithmetic (logical) function symbols only have arithmetic (logical)
arguments.
For example, this excludes N ∧ 80.000 as a correct expression.
Strongly typed genetic programming (STGP) addresses this issue.
The most common implementation of tree-based mutation works as follows:
Select a node at random from the tree.
Replace the sub-tree starting there with a randomly generated
tree.
This newly created sub-tree is usually generated the same way as in the
initial population.
It is also subject to conditions on maximum depth and width.
The image illustrates how the parse tree example above (left) is mutated
into one standing for \(2 \cdot \pi + ((x + 3)
- y)\).
As one goes down through a tree there are potentially more nodes at any
given depth.
Size
The size, or tree depth, of the child can exceed that of the parent
tree.
In this regard, mutation within GP differs from mutation in other EC
dialects.
Tree-based mutation is illustrated here:
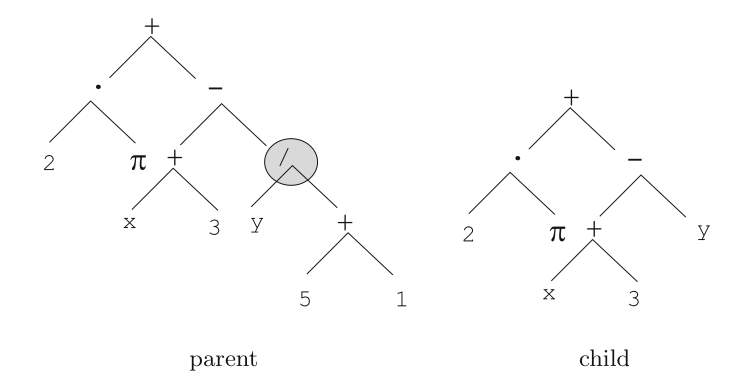
The node designated by a circle in the tree on the left is selected for
mutation.
The sub-tree staring at that node is replaced by a randomly generated
tree, which is a leaf here.
Tree-based mutation has two parameters:
First, the probability of choosing mutation itself, instead of, or in
addition to, recombination, pm
Second, the probability of choosing an internal point within the parent
as the root of the sub-tree to be replaced.
It is remarkable that Koza’s classic book on GP from 1992 advises
users to set the mutation rate at 0.
This suggests GP works without mutation!
More recently Banzhaf et al. recommended 5%.
In giving mutation such a limited role, GP differs from other EA
streams.
The generally shared view is that crossover has a large shuffling
effect, acting in some sense, as a macro-mutation operator.
The current GP practice uses low, but positive, mutation
frequencies,
even though some studies indicate that the common wisdom favoring an
(almost) pure crossover approach might be misleading.
Tree-based recombination creates offspring by swapping genetic
material among the selected parents.
It is a binary operator, taking two parent trees, to create two child
trees.
The most common implementation is sub-tree crossover.
Start at two randomly selected nodes in the given parents.
Each node is a sub-tree.
Interchanging those two sub-trees.
Size
Like in mutation, size (tree depth) of the children can exceed that of
the parent trees.
In this regard, recombination within GP differs from recombination in
other EC dialects.
Tree-based recombination has two parameters:
First, the probability of choosing recombination at the junction with
mutation, pc
Second, the probability of choosing internal nodes as crossover
points
Tree-based crossover is illustrated here:
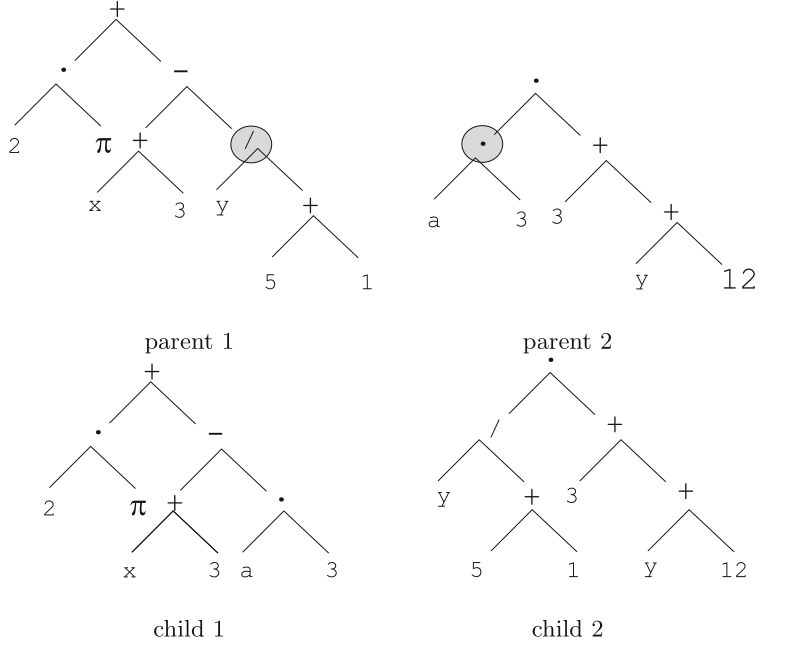
The nodes designated by a circle in the parent trees are selected to
serve as crossover points.
The sub-trees staring at those nodes are swapped, resulting in two new
trees, which are the children.
We’ll cover this representation more with genetic programming, near
the end of this class:
GeneticProgramming.html