
https://www.xkcd.com/1739/
Show self-recording screencast to start.
Lecture start/end points are noted below in the notes.
* Lecture 1: https://vimeo.com/521071999
* Lecture 2: https://vimeo.com/522062744
* Tip: If anyone want to speed up the lecture videos a little, inspect
the page, go to the browser console, and paste this in:
document.querySelector('video').playbackRate = 1.2
https://realpython.com/python-thinking-recursively/
https://www.python-course.eu/python3_recursive_functions.php
https://en.wikipedia.org/wiki/Recursion
As with any constructive discussion, we start with definitions:
“To understand recursion, you must understand
recursion.”

What is base case above?
https://en.wikipedia.org/wiki/Recursive_acronym
GNU: GNU’s Not Unix
YAML: YAML Ain’t Markup Language (initially “Yet Another Markup
Language”)
WINE: WINE Is Not an Emulator
https://www.google.com/search?&q=recursion (notice
the: “Did you mean recursion?”)
The first line of these definitions may seem circularly
dissatisfying.
It is the second line that grounds these definitions, making them
useful.
https://en.wikipedia.org/wiki/Natural_number
For example, 1, 2, 3, 4, …
Natural numbers are either:
n + 1, where n is a natural number, or
1
https://en.wikipedia.org/wiki/Exponentiation
For example, 28 = 256
Exponentiation:
bn = b * bn-1, or
b0 = 1
https://en.wikipedia.org/wiki/Factorial
For example,
5! = 5 × 4 × 3 × 2 × 1 = 120
Factorial:
n! = n * ((n - 1)!), or
0! = 1
Recursion in computer science is a self-referential
programming paradigm,
as opposed to iteration with a while() or for() loop, for
example.
Concretely, recursion is a process in which a function calls
itself.
Often the solution to a problem can employ solutions to smaller
instances of the same problem.
You’re not just decomposing it into parts, but incrementally smaller
parts.
Condition or test, often an if(), which tests for
a
base case (which often results in termination), which
only executes once, after doing the
recursive case repeatedly
14-Recursion/recursion_00_exp.py
Check out code now!
We can use an accumulator variable, starting at low values, working our
way up.
What is the big theta of this function?
What is the number of iterations for for n = 1, n = 2, n = 3?
++++++++++++++++++
Cahoot-14.1
Ask: What is 2^-8 ^?
Check out code now!
We use a trivial one-layer recursion.
A recursive call is like regular function calls!
How many activation records exist on the stack?
Show the stack in the debugger.
The recursive case looks just like your mathematical definition.
Recursive case:
bn = b * bn-1
Base case (termination):
b0 = 1 (or slightly faster, though less “correct”:
b1 = b)
Condition/test, which checks for the base:
if(n == 0):
For example:
b4 =
b * b3 =
b * (b * b2) =
b * (b * (b * b1)) =
b * (b * (b * (b * b0)))
When does the first function call actually finish?
Actually trace code now!
Unlike the iterative algorithm, which accumulates a value up, recursion
starts at the top values, and works down.
In the debugger, watch the activation records on the stack, count them
as we trace.
What is the big theta of this function?
Recursion depth for n = 1, n = 2, n = 3?
Real-world example:
Exponentiation is used very frequently in big-cryptography.
Imagine you have a web-server that makes 1 million connections a
day.
Some bitcoin server farms have power bills in the many millions per
month!!
How many dollars in power bills, or carbon dioxide production could you
save,
with just an improvement from an improvement from a big theta of n to
log2(n)??
To obtain bn, do recursively:
if n is even, do bn_2 * bn_2
if n is odd, do b * bn_2 * bn_2
with base case, b1 = b
where n//2 is integer (floor) division
What is b62** ?**
What is b61** ?**
How many multiplications when counting from the bottom up?
Check out the code now.
What is the maximum number of activation records on the stack for a
given n?
Display the printed output to show how many fewer multiplications there
are!
++++++++++++++++++
Cahoot-14.2
Paying attention to order of code around recursive calls is
important!!
When a function calls itself,
instructions placed before the recursive call are executed once per
recursion,
before the next call, “on the way down the stack”.
Instructions placed after the recursive call are executed
repeatedly,
after the maximum recursion has been reached, “on the way up the
stack”.
Observe code:
14-Recursion/recursion_01_order.py
Stack of what?
Check out the stack in pudb3.
The state of execution when you call a new function is still waiting
when you get back to it!
A slow complexity class, but computing factorial itself is not too slow (these are different concepts).
Recursive case:
n! = n * ((n - 1)!)
Base case (termination):
0! = 1
Condition/test, which checks for the base:
if(n == 0):
Observe code
Example:
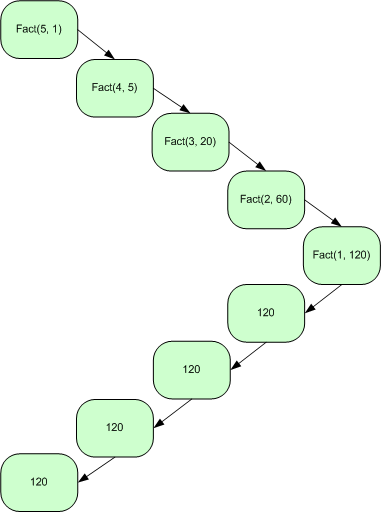
Factorial n! = n * ((n - 1)!)
0! = 1
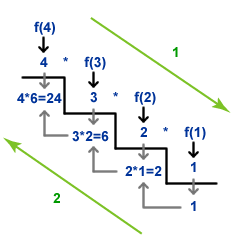
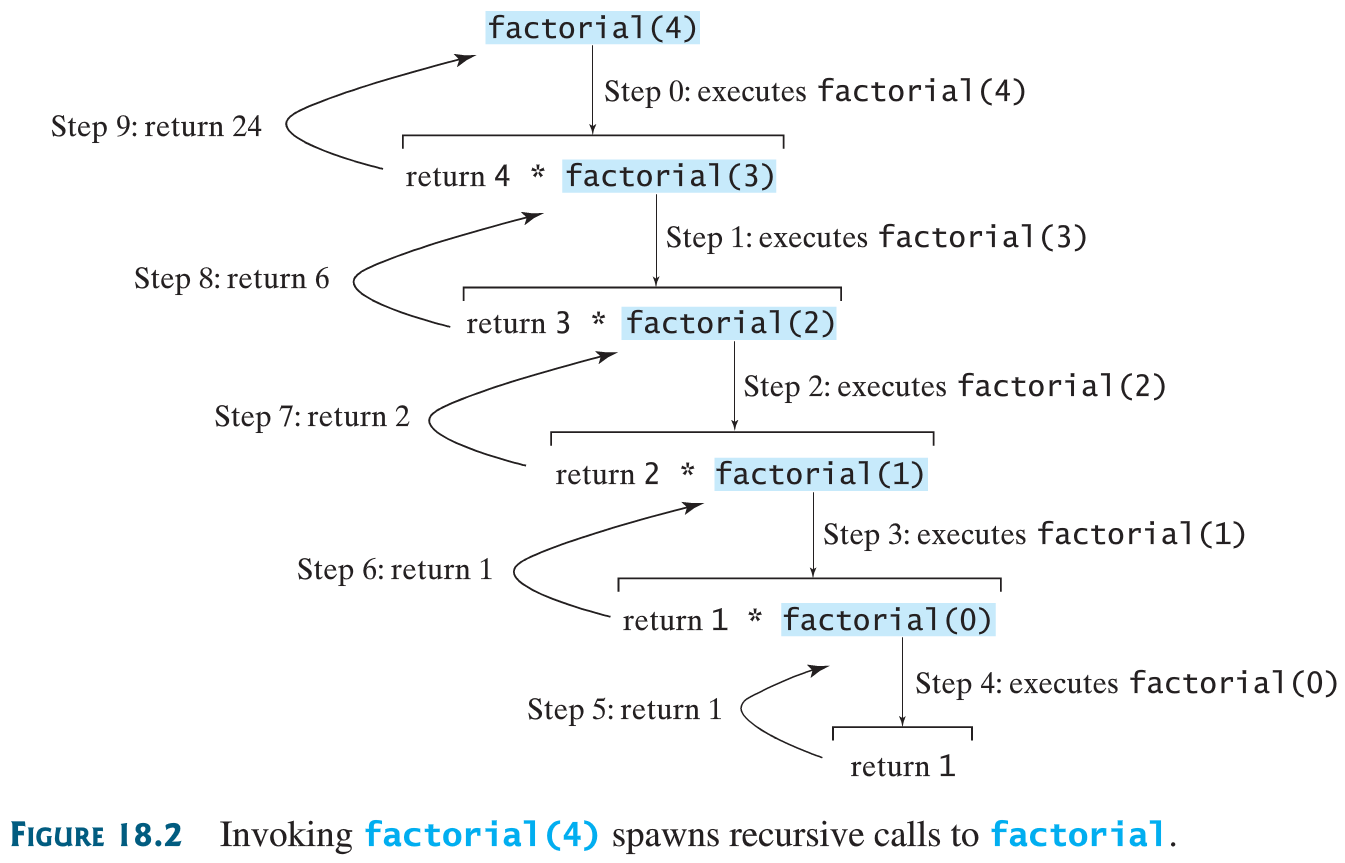
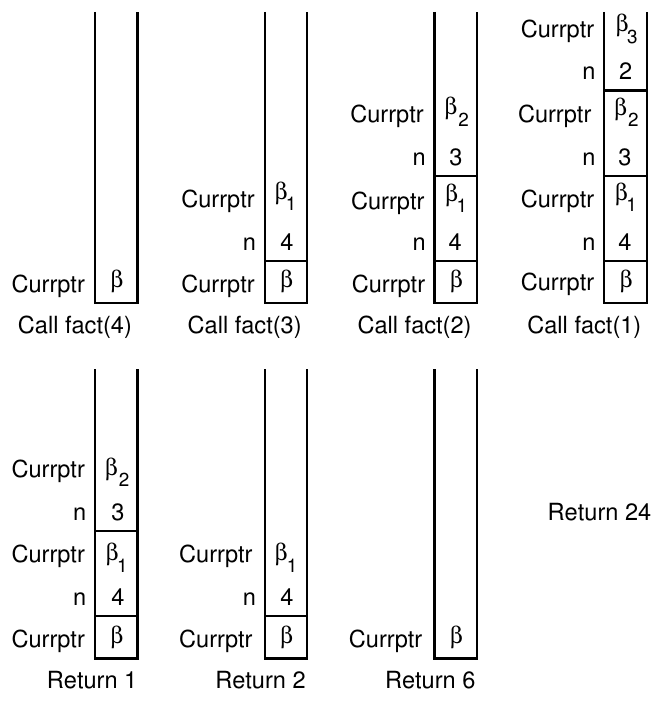
Observe code, and evaluate calling factorial of 3:
14-Recursion/recursion_02_factorial.py
Since 3 is not 0, take second branch and calculate (n-1)!...
Since 2 is not 0, take second branch and calculate (n-1)!...
Since 1 is not 0, take second branch and calculate (n-1)!...
Since 0 equals 0, take first branch and return 1.
Return value, 1, is multiplied by n = 1, and return result.
Return value, 1, is multiplied by n = 2, and return result
Return value, 2, is multiplied by n = 3, and the result, 6, becomes the
return value of the function call that started the whole process.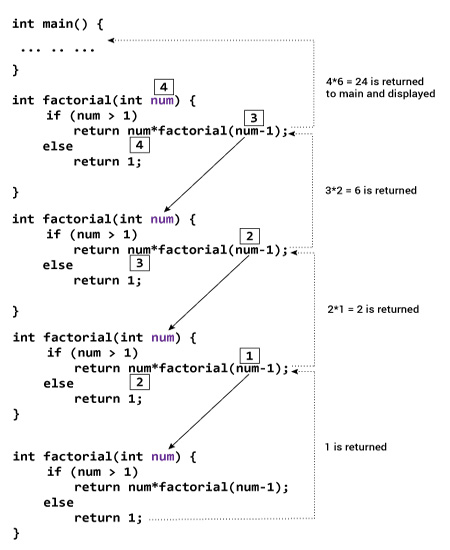
What happens when I run this??
14-Recursion/recursion_03_uh_o.py
Actually run this… As you can see, recursion is the bomb!
“Wherever you go, there you are.”
- https://en.wikipedia.org/wiki/Jon_Kabat-Zinn
Recursive side note:
One concrete definition of consciousness or awareness is
meta-cognition,
a form of self-referential thought.
https://en.wikipedia.org/wiki/Call_stack
Manages the stack of activation records.
A Call stack is a stack data structure that stores
information,
about the active subroutines (functions) in a computer program.
A subroutine/function call is implemented by placing necessary
information about the subroutine
(including the return address, parameters, and local variables) onto
“the stack”.
It is also known as:
the execution stack, program stack, control stack, run-time stack, or
machine stack,
and is often shortened to just “the stack”.
Information associated with one function call is called an
activation record or stack
frame.
Further subroutine calls add more records / frames to the stack.
Each return from a subroutine pops the top activation record off the
stack.
Although maintenance of the call stack is important for the proper
functioning of most software,
the details are normally hidden and automatic in high-level programming
languages.
In python, it is managed invisibly “behind the scenes”,
though you can directly inspect or manipulate it, if you want.
You can peek into the back-end by using pudb3 to see the
stack.
When viewing the stack in pudb3,
which activation records are most shallow, and which are most deep?
Observe these while tracing:

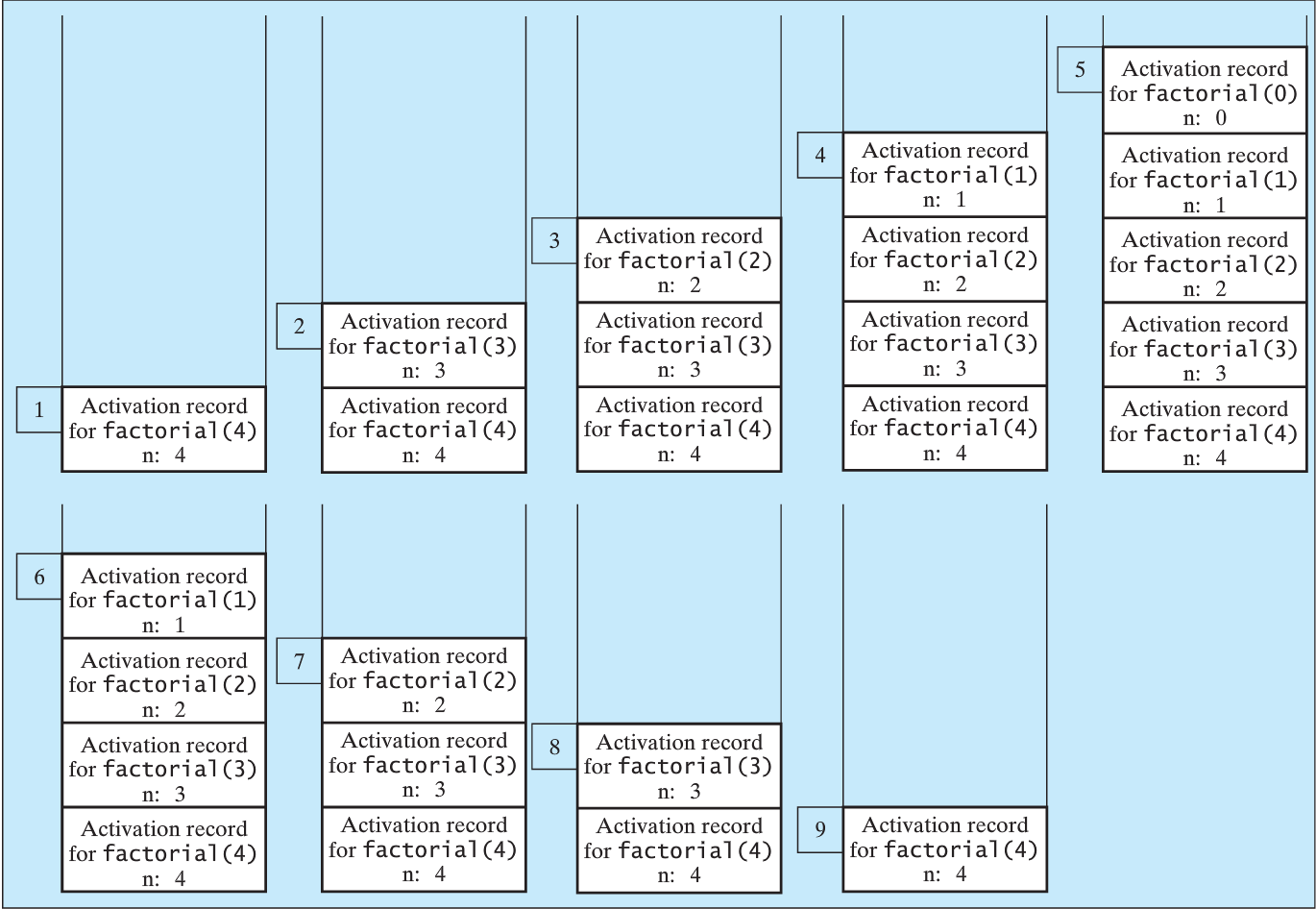
Each record on the stack needs a return address (more on this in years to come).
In practice, a recursive call doesn’t make an entire new copy of a
routine.
Each function call is assigned a chunk of memory to store its activation
record where it:
Records the location to which it will return.
Re-enters the new function code at the beginning.
Allocates memory for the local data for this new invocation of the
function.
… until the base case, then:
Returns to the earlier function right after where it left off…
Recursive programming variations: a partial overview
Single recursion:
Contains a single self-reference
e.g., list traversal, linear search, or computing the factorial
function…
Single recursion can often be replaced by an iterative
computation,
running in linear (n) time and requiring constant space.
Multiple recursion (binary included):
Contains multiple self-references, e.g., tree traversal, depth-first
search (coming up in future courses)…
This may require exponential time and space, and is more fundamentally
recursive,
not being able to be replaced by iteration without an explicit
stack.
Multiply recursive algorithms may seem more inherently recursive.
Some of the slowest complexity-class functions known are multiply
recursive;
some were even designed to be slow!
Indirect (or mutual) recursion:
Occurs when a function is called not by itself,
but by another function that it called (either directly or
indirectly).
Chains of 2, 3, …, n functions are possible.
Generative recursion:
Acts on outputs it generated (e.g., a mutated mutable List).
Structural recursion:
Acts on progressive newly generated sets of input data (e.g., a copied
immutable string).
A single linear self-reference.
As above, this is another way to define factorial:
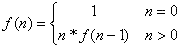
The first line is the base case.
The second line is the recursive call.
Notice that the recursive call to f() does NOT contain all
statements.
Specifically n * resides outside the call.
Example call-tree for factorial definition:
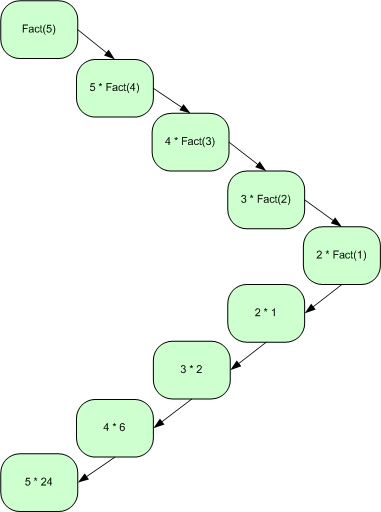
Where the recursive call contains all computation, and mimics iteration.
Factorial definition with tail-call design:
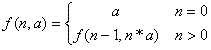
The first line is the base case.
The second line is the recursive case.
Notice that the recursive call to f() contains all statements, with none
outside f().
This mimics an iterative construction in some way.
Example call-tree for tail-call factorial definition:
This is potentially more efficient.
A function that calls a friend, that calls it back.
A pair of functions that each return a Boolean:
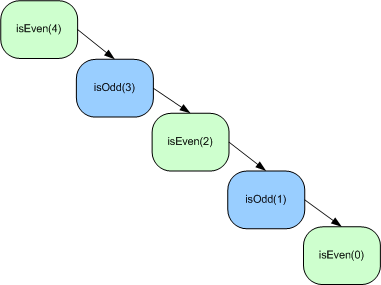
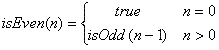
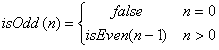
This is an inefficient way to check for even or odd numbers…
To expand on that side note, check out the code:
14-Recursion/recursion_04_thats_odd.py
(a kind of multiple recursion)
https://en.wikipedia.org/wiki/Fibonacci_number
Fibonacci sequence definition:
Base case:
F0 = 0,
F1 = 1
Recursive case:
Fn = Fn-1 + Fn-2
Unpacked:
1, 1, 2, 3, 5, 8, 13, …
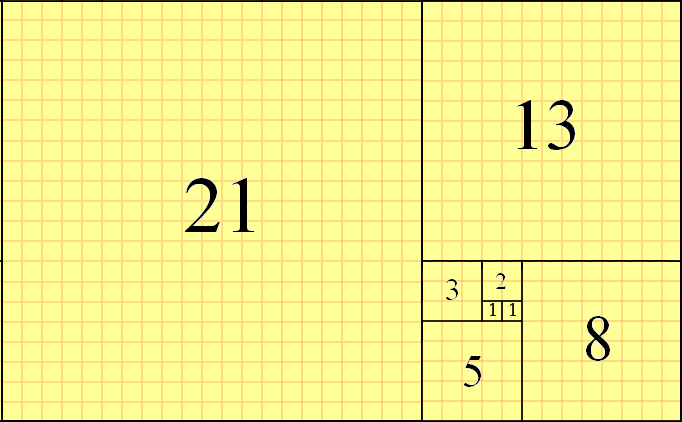
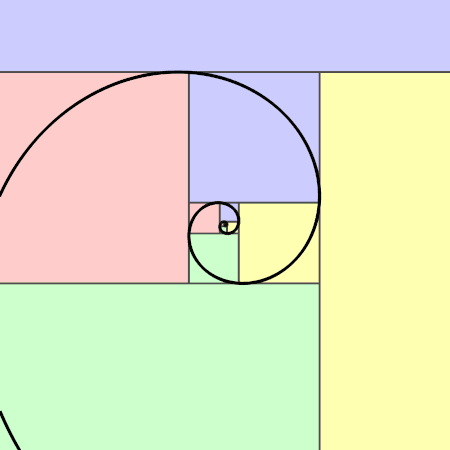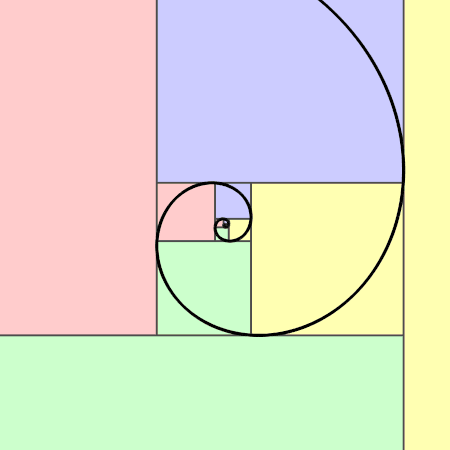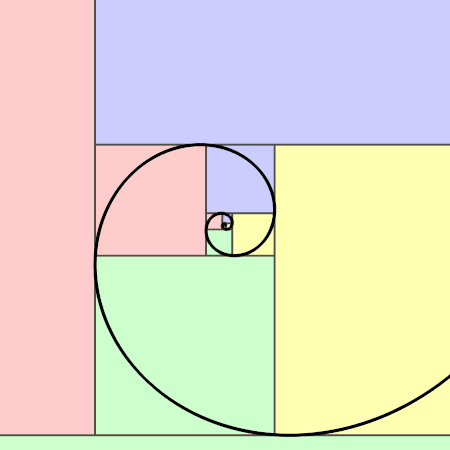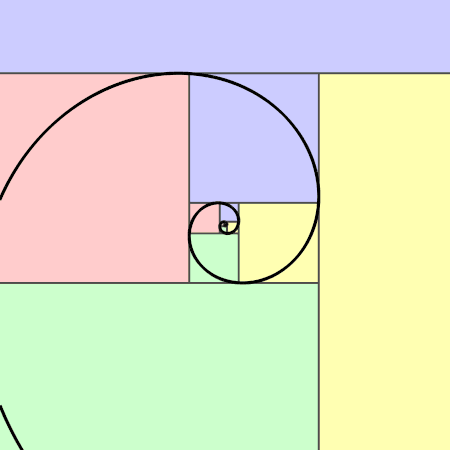
Functional set-notation definition:
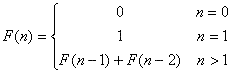
What the call-tree could look like:
Do you see any problems here?
Wait on code trace for this function until efficiency section below.
“To create recursion, you must create recursion.”

First design and write the base case(s) and the
conditions to check it!
You must always have some base case(s), which can be solved without
recursion.
Think about solving the problem by combining the results of one
or more smaller, but similar, sub-problems.
If the algorithm you write is correct,
then certainly you can rely on it (recursively) to solve the smaller
sub-problems.
You’re not just decomposing it into parts, but incrementally smaller
parts.
Make real progress
For the cases that are to be solved recursively,
the recursive call must always be to a future case,
that makes a fixed quantity of progress toward a base
case (not fixed proportion).
What happens if you always get half closer to something?
Check progressively larger inputs to inductively
validate that there is no infinite recursion
Proof of correctness by induction?
Can you satisfy to yourself that it works on a problem of size 0, 1, 2,
3, …, n?
Do not worry about how the recursive call solves the
sub-problem.
Simply accept that it will solve it correctly,
and use this result to in turn correctly solve the original
problem.
Compound interest guideline:
Try not to duplicate work by solving the same instance of a problem in
separate recursive calls.
Of recursion in code.
There are a variety of ways to reverse an ordered container.
We can use recursion to use the input/output buffer to reverse inputted
text.
Recall, variables operated on before the recursive call appear on the
way down the stack,
while those being operated on after the recursive call appear after the
base case, on the way up the stack.
Remember, as we unwind off the stack, the values of the variables are
where we left them.
Check out code now:
14-Recursion/recursion_05_reverse.py
https://en.wikipedia.org/wiki/Palindrome
Base case (which often results in termination)?
If we assume that we must have incrementally smaller versions of the
problem, does this lead us to our base case?
Is the string ’’ a palindrome?
is the string ‘a’ a palindrome?
Recursive case?
What is the one-smaller version of a palindrome problem?
Do we work from the inside or outside?
What is the condition/test that checks for the base?
What is a check for a one-smaller version of the palindrome problem?
Observe code to show recursion stack:
14-Recursion/recursion_06_palindrome.py
Cool side-note: we use greedy boolean comparisons to quit early
(efficiently)!
++++++++++++++++++
Cahoot-14.3
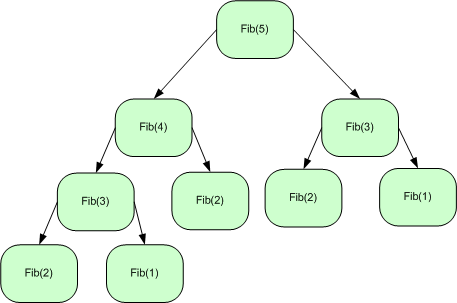
Euclid’s algorithm efficiently computes the greatest common divisor (GCD) of two numbers (AB and CD below), the largest number that divides both without leaving a remainder (CF).
Proceeding left to right:
Check out the code, loop then recursive:
14-Recursion/recursion_07_gcd.py
Which is more efficient, and by how much?
After 2 iterations, rem is at half its original value.
If ab > cd, then ab % cd < ab / 2.
Thus, the number of iterations is at most log n.
++++++++++++++++++
Cahoot-14.4
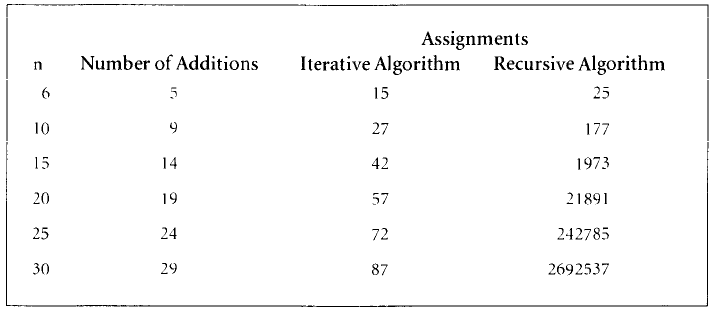
Add all the numbers in a list of ints.
See code: Iterative versus Recursive.
Recursive case: What is an incrementally smaller version of the sum
problem?
Base case: What is the smallest termination condition?
14-Recursion/recursion_08_sum.py
Could we convert from the iterative version to the recursive?
“Progress isn’t made by early risers.
It’s made by lazy men trying to find easier ways to do
something.”
- https://en.wikipedia.org/wiki/Robert_A._Heinlein
Are there any disadvantages to recursion?
What overhead is involved when making a function call?
save caller’s state
allocate stack space for arguments
allocate stack space for local variables
invoke routine at exit (return), release resources
restore caller’s “environment”
resume execution of caller
Much of this is language-dependent.
A few (but not all) recursive functions can be unnecessarily
inefficient,
and would be better implemented as iterative functions.
For example, our first recursive Fibonacci implementation has a steep computational complexity (is less efficient) than our iterative solution, no fibbing:
if n is zero, then fib(n) is: 0if n is one, then fib(n) is: 1
else, fib(n) is: fib(n - 1) + fib(n - 2)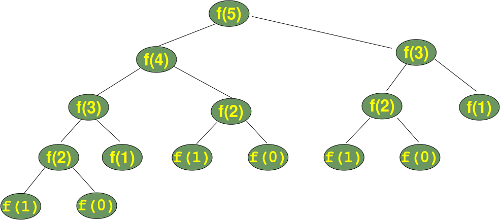
Observe recursive code:
14-Recursion/recursion_09_loop_to_recursion_fibonacci.py
Step f(3) all the way deep.
When you step a multiply recursive line, which gets called first, left
or right?
This algorithm produces something like a depth-first enumeration of the
above tree.
While it is nice that the python code looks like our mathematical
definition, it is inefficient!
How long does fib_rec(35) take?
How many iterations?

How long does fib_loop(35) take?
How many iterations?
There are a number of solutions to this problem of efficiency:
If you can easily find a looping algorithm
(e.g., Fibonacci with a loop below)
Observe iterative code.
The larger the n, the worse the recursive solution becomes, in
comparison to the iterative.
This is what it means to have a worse complexity.
Remember, recursion is just another way to loop.
Successfully designing an iterative algorithm to replace a recursive one
is not always easily possible.
Tail recursion is much like looping.
Often, but not always, developing tail recursive implementation,
may follow first writing an iterative solution.
++++++++++++++++++
Cahoot-14.5
“There is nothing so useless as doing efficiently that which
should not be done at all.”
- https://en.wikipedia.org/wiki/Peter_Drucker
is just a glorified loop.
Tail call is a subroutine call performed as the final action of a
procedure (recall order mattering example).
Tail calls don’t have to add new stack frame to the call stack.
Tail recursion is a special case of recursion,
where the calling function does no more computation after making a
recursive call.
Tail-recursive functions are functions in which all recursive calls are
tail calls,
and thus do not build up any deferred operations.
Producing such optimized code instead of a standard call sequence is
called tail call elimination.
Tail call elimination allows procedure calls in tail position to be
implemented as efficiently as goto statements,
thus allowing more efficient structured programming.
converts an iterative loop into a tail recursion.
Systematic steps:
1. First identify those variables that exist outside the loop, but are
changing in the loop body; these variable will become formal parameters
in the recursive function.
2. Then build a function that has these “outside” variables as formal
parameters, with default initial values.
3. The original loop test becomes an if() test in the body of the new
function.
4. The if-true block becomes the needed statements within the loop and
the recursive call.
5. Arguments to the recursive call encode the updates to the loop
variables.
6. else block becomes either the return of the value the loop attempted
to calculate (if any), or just a return.
7. Conversion results in tail recursion.
Code examples:
See multiple examples in code (fib, fact, countdown),
match them to the above steps in detail.
This is really cool.
It is a systematic way to convert any loop to recursion,
by just following those above steps in rote form!
14-Recursion/recursion_10_loop_to_recursion_factorial.py
14-Recursion/recursion_11_loop_to_recursion_countdown.py
A future lab in this class will involve solving several problems
iteratively and recursively.
For each problem, you will implement one iterative solution and one
recursive solution.
To program the recursive solution, you could either:
1. Implement a natural recursive solution by inventing one creatively,
or
2. Implement an iterative solution, and then perform the above
systematic conversion to use tail-call recursion from your iterative
solution.
Language choice gcc-c++ (aka g++) can usually do tail call
optimization.
Tail call elimination doesn’t automatically happen in Java or
Python,
though it does reliably in functional languages like Lisps:
Scheme, Clojure (upon specification with recur only), and
Common Lisp,
which are designed to employ this kind of recursion.
https://en.wikipedia.org/wiki/Memoization
Memoization and caches (stores) the values which have
already been computed,
rather than re-compute them.
It speeds up computer programs, by storing the results of expensive
function calls,
and returning the cached result when the same inputs occur again.
See code for Fibonacci
14-Recursion/recursion_12_memoization_dynamic_prog.py
This kind of memoization is a form of dynamic
programming,
which is really a terrible name, because it’s much more like static
programming:
one definition (there are others) is that you store values instead of
re-computing them,
in a trade-off between space complexity (storage) and time complexity
(CPU cycles):
https://en.wikipedia.org/wiki/Dynamic_programming#Computer_programming
In the trace, load up a full dictionary for fib_mem,
which does something like a depth-first population of the
dictionary!
This is the most recursion-friendly solution so far,
and works for essentially any recursive program,
even those that can’t easily be converted to a loop.
Conversion of recursive functions to loops is:
less systematic than converting a loop to tail recursive,
requires more creativity, and
isn’t always easy for a human,
though converting an already tail recursive algorithm is more
straightforward.
Often converting more inherently recursive algorithms to loops
requires keeping a programmer-designed stack,
like would be done by the compiler in the first place.
See example for factorial (C++ examples from 1575 only for now; no
stacks in CS1500)…
“Life can only be understood backwards;
but it must be lived forwards.”
- https://en.wikipedia.org/wiki/S%C3%B8ren_Kierkegaard
Recursion is not just for toy examples.
What kind of algorithms are realistically implemented using
recursion?
There are many algorithms that are simpler or easier to program
recursively,
for example tree enumeration algorithms (which we cover later in in the
data structures course).
Tree traversal is the most common real-world use of recursion.
Some recursive algorithms are actually more efficient (for example,
exponentiation).
Some algorithms were invented recursively,
and no one has figured out an equivalent iterative algorithm
(other than a trivial stack conversion like the compiler or interpreter
uses).
What about some more realistic algorithm?
We covered binary search using loops on our last lecture:
13-AlgorithmsSoftware.html
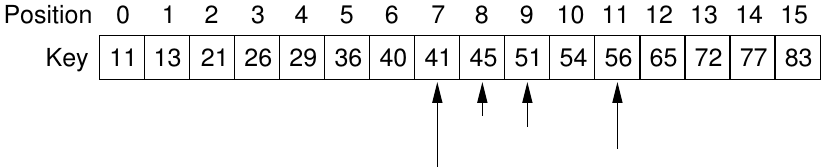
How might we implement this form of search recursively?
What is the base case?
What is the incrementally smaller case?
What is the condition?
See code:
14-Recursion/recursion_13_binary_search.py
https://en.wikipedia.org/wiki/Backtracking
Backtracking finds all (or some) solutions to some computational
problems,
notably constraint satisfaction problems,
by incrementally building candidates to the solutions,
and abandoning a candidate (“backtracking”),
as soon as it determines that the candidate cannot possibly be completed
as a valid solution.
It is actually what is known as a general
meta-heuristic, rather than an algorithm:
https://en.wikipedia.org/wiki/Metaheuristic
This is in-part because you can use the meta-heuristic to wrap
algorithms for a variety of problems,
with slight modifications.
How do you fix your past mistakes??
You are faced with repeated sequences of options and must choose one
each step.
After you make your choice you will get a new set of options.
Which set of options you get depends on which choice you made.
Procedure is repeated until you reach a final state.
If you made a good sequence of choices, your final state may be a goal
state.
If you didn’t, you can go back and try again.
For example, games such as: n-Queens, Knapsack problem, Sudoku, Maze, etc.
Backtracking is a general meta-heuristic that incrementally builds
candidate solutions,
by a sequence of candidate extension steps, one at a time,
and abandons each partial candidate, c, (by backtracking),
as soon as it determines that c cannot possibly be extended to a valid
solution.
can be completed in various ways, to give all the possible solutions to
the given problem.
can be implemented with a form of recursion, or stacks to mimic
recursion.
refers to the following procedure:
If at some step it becomes clear that the current path that you are on
can’t lead to a solution,
then you go back to the previous step (backtrack) and choose a different
path.
Pick a starting point.
recursive_function(starting point)
If you are done (base case), then
return True
For each move from the starting point,
If the selected move is valid,
select that move,
and make recursive call to rest of problem.
If the above recursive call returns True, then
return True.
Else
undo the current move
If none of the moves work out, then
return FalseYou can use this meta-heuristic to solve a whole variety of problem types.
++++++++++++++++++
Cahoot-14.6
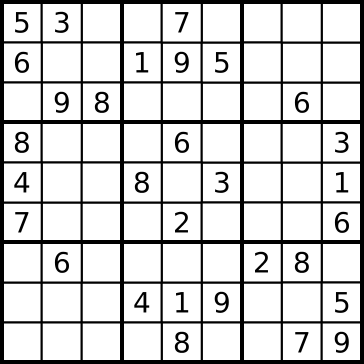
We’ll go over Sudoku and maze-navigation now:
https://en.wikipedia.org/wiki/Sudoku
Starting board (not initial configurations all are solvable, but this
one is):
Finish (win):

Board is 81 cells, in a 9 by 9 grid.
with 9 zones, each zone being:
the intersection of the first, middle, or last 3 rows, and the first,
middle, or last 3 columns.
Each cell may contain a number from one to nine;
each number can only occur once in each zone, row, and column of the
grid.
At the beginning of the game, some cells begin with numbers in
them,
and the goal is to fill in the remaining cells.
Exercises:
What would be your human Sudoku strategies?

How might we solve this non-recursively (iteratively)?
Where would you start?
What might you loop across?
How would you end?
What sub-functions might you want?

How about recursively?
What is the base case?
What is an incrementally smaller version?
What is the condition/check?
Which functions do we need (do they overlap from the iterative version
we drafted above)?
recursive_sudoku()
Find row, col of an unassigned cell, an open move
If there are no free cells, a win, then
return True
For digits from 1 to 9
If no conflict for digit at (row, col), then
assign digit to (row, col)
recursively try to fill rest of grid
If recursion successful, then
return True
Else
remove digit
If all digits were tried, and nothing worked, then
return FalseMy code for Sudoku:
14-Recursion/recursion_14_sudoku.py
Note: I originally wrote this for C++, and then converted it to python,
so this python code has a bit of a C-style to it.
As we trace this, pay attention to:
diving deeper by stepping,
the first time backtracking happens,
look-ahead versus look-behind,
whether a function call is responsible for reversing it’s own move, or
the move of another function call,
the final termination condition.
Your maze’s code macro-structure can be essentially identical to the
Sudoku code above.
If it diverges, you should fix it to match what I’ve given here!!
++++++++++++++++++
Cahoot-14.7
https://en.wikipedia.org/wiki/Maze_solving_algorithm
https://en.wikipedia.org/wiki/Maze#Solving_mazes
General rules to solve a maze?
How about the right or left hand rule?
Start in center, and try to escape:
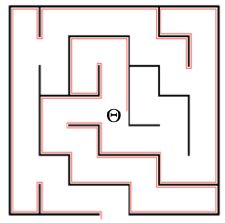
General rules to solve a maze?
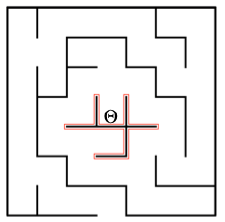
Right or left hand rule doesn’t work with this kind of loop:
Recursive maze-finding:
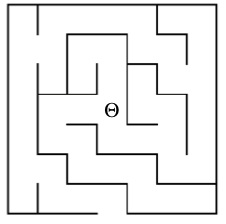
What is the base case?
What is an incrementally smaller version of the maze problem?
What is the condition?
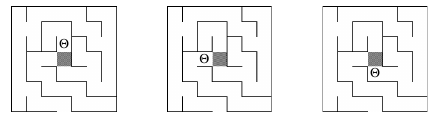
Maze with prize at center Goal:
start outside of maze, obtain prize, find your way out.

Important note:
Use the pseudo-code and the Sudoku code to write your maze!
Don’t copy code from the internet…