“The enemy knows the system”
https://en.wikipedia.org/wiki/Kerckhoffs's_principle
a.k.a Shannon’s maxim:
“A cryptosystem should be secure even if everything about the
system,
except the key, is public knowledge.”
Discussion questions:
Why do you think this is a difficult notion for newcomers to
cryptography?
Is the below similar statement true?
If everything about the system, except the key, is not public knowledge,
is the system secure?
Is it trustworthy?
How does trust relate to security?
How are they different?
https://proprivacy.com/guides/why-open-source-is-so-important
document.querySelector('video').playbackRate = 1.2http://inventwithpython.com/cracking/ Chapters 13-15
Today, we will go over two encryption algorithms which use some of the basic math we will rely on for modern cryptography, Diffie-Helmen and RSA for example.
https://en.wikipedia.org/wiki/Modular_arithmetic

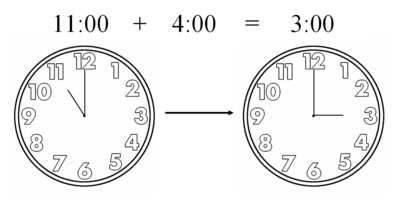
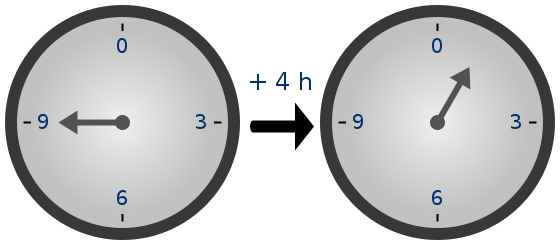
(11 + 4) % 12 = 3
(10 + 200 hours) % 24 = 6
The mod operator, %, works this way:
a mod b is the remainder after a is divided by b.
For example:
7 % 3 is 1 (since 7 / 3 is 2 with remainder 1).
27 % 3 is 0 (since 27 / 3 is 9 with remainder 0).
4 % 7 is 4 (since 4 / 7 is 0 with remainder 4).
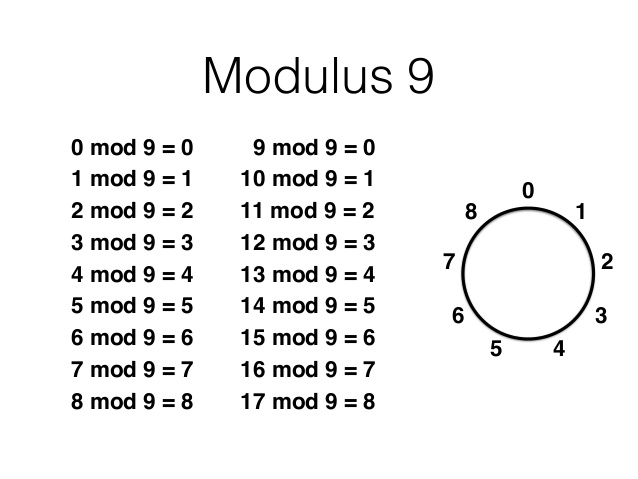
Defining a Ring mod 9:
Modular arithmetic can be handled mathematically,
by introducing a congruence relation on the integers,
that is compatible with the operations on integers, including:
addition, subtraction, multiplication, and what
else?
For a positive integer n,
two numbers a and b are said to be congruent modulo
n,
if their difference a - b is an integer multiple of
n
(that is, if there is an integer k such that a − b =
kn).
This congruence relation is typically considered when a and
b are integers,
and is denoted:
\(a\equiv b \pmod {n}\)
The number n is called the modulus of the congruence.
The congruence relation may be rewritten as:
\(a=kn + b\)
The following:
\(a\equiv b \pmod {n}\)
asserts that a and b have the same remainder when
divided by n.
That is:
\(a = p n + r\)
\(b = q n + r\)
Example:
\(38 \equiv 14 \pmod {12}\)
because 38 - 14 = 24, which is a multiple of 12, or
equivalently,
because both 38 and 14 have the same remainder 2 when divided by 12.
How do you ask what time it was 40 hours ago?
Reversing addition (mod m) is performed with subtraction (mod
m),
to produce the equivalent “ring” like effect as addition,
including the modulus of negative numbers.
For example, in the Caesar cipher we went over previously:
IntroCryptoCaesar.html
One can multiply a number mod m.
Multipliplication should still be consistent, mod m:
\(a*b \equiv c \pmod m\)
For example:
\(5*6 \equiv 2 \pmod 7\)
Reversing multiplication mod m is more complicated!
The normal division, that you are used to,
is defined as the inverse of multiplication.
a * b = c
c / b = a
We can also define something like the following to be true (mod
m):
\(a*b \equiv c \pmod m\)
then:
\(c/b \equiv a \pmod m\)
For example, multiplication:
5 * 6 = 30, which leaves a remainder of 2 when divided by 7, and
thus:
\(5*6 \equiv 2 \pmod 7\)
and the complementary division:
\(2/6 \equiv 5 \pmod 7\)
Usually, instead of using division,
we’ll multiply using something called a modular multiplicative
inverse.
The modular inverse of n is a number,
that when multiplied with n, is 1.
This is just like the inverse of a number in regular
arithmetic:
\(x * (1 / x) = 1\)
It also has an interesting property:
Multiplying anything times 1 equals that thing.
This will be one CRITICAL point in understanding RSA,
an asymmetric encryption algorithm we will cover later.
https://en.wikipedia.org/wiki/Modular_multiplicative_inverse
The modular multiplicative inverse of an integer a,
is an integer x such that the product a * x is
congruent to 1,
with respect to the modulus m.
In the standard notation of modular arithmetic,
this congruence is written as:
\(ax \equiv 1 \pmod {m}\)
which is a shorthand way of writing the statement that:
m divides (evenly) the quantity a * x − 1,
or put another way:
the remainder after dividing a * x by the integer m is
1.
a times what is 1 with mod m?
This is a special case of a linear congruence:
Where b is non-1, and a and m are given,
\(ax \equiv b \pmod {m}\)
there may be zero or multiple solutions for x.
(specified values of a and x for some b and m, satisfying the
equation),
but when \(ax \equiv 1 \pmod
{m}\),
then there can be provably only one solution.
Such a solution exists, if and only if
\(gcd(a, m) = 1\), that is,
a and m must be relatively prime (i.e. co-prime).
Further, when this condition holds, there is exactly one
solution,
i.e., when it exists, a modular multiplicative inverse is unique.
Why is the above nuance interesting??
Here is another example to explore this further:
Two integers are congruent mod 10,
if and only if their difference is divisible by 10,
for example:
\(32 \equiv 12 \pmod {10}\) since 10
divides 32 − 12 = 20, and
\(111 \equiv 1 \pmod {10}\) since 10
divides 111 − 1 = 110.
With a and m given, a mod inverse is defined as:
(a * i) % m = 1,
where i is the modular inverse.
For example, the modular inverse of 5 (mod 7) would be some number
i,
where:
(5 * i) % 7 = 1.
You can brute-force this calculation like this:
Because (5 * 1) % 7 = 5,
1 isn’t the modular inverse of 5 mod 7
Because (5 * 2) % 7 = 3,
2 isn’t the modular inverse of 5 mod 7
Because (5 * 3) % 7 = 1,
3 is the modular inverse of 5 mod 7
Not every element of a complete residue system modulo m has a modular
multiplicative inverse,
for example, zero never does.
After removing the elements of a complete residue system that are not
relatively prime to m,
what is left is called a reduced residue system,
all of whose elements have modular multiplicative inverses.
The number of elements in a reduced residue system is defined as:
\(\phi(m)\)
where \(\phi\) is the Euler totient
function.
Euler’s totiennt defines the number of positive integers less than
m,
that are relatively prime to m.
Given a and m, to find x efficiently
(if it exists, which necessarily occurs only when \(gcd(a, m) = 1\)),
we use the Extended Euclidean formula:
https://en.wikipedia.org/wiki/Extended_Euclidean_algorithm
A modular multiplicative inverse of a modulo
m can be found analytically.
For this purpose, we use the extended Euclidean algorithm.
Note: Skim this now, more depth later.
Code:
AffineCipher/cryptomath.py
# Cryptomath Module
# https://www.nostarch.com/crackingcodes (BSD Licensed)
from typing import Optional
def gcd(a: int, b: int) -> int:
"""
Euclid's Algorithm
Return the Greatest Common Divisor of a and b
"""
while a != 0:
a, b = b % a, a
return b
def findModInverse(a: int, m: int) -> Optional[int]:
# Return the modular inverse of a % m, which is
# the number x such that a*x % m = 1
if gcd(a, m) != 1:
# Ah dynamic typing!
return None
# No single mod inverse exists if a & m aren't relatively prime.
# Calculate using the Extended Euclidean Algorithm:
u1, u2, u3 = 1, 0, a
v1, v2, v3 = 0, 1, m
while v3 != 0:
# Note that // is the integer division operator
q = u3 // v3
v1, v2, v3, u1, u2, u3 = (u1 - q * v1), (u2 - q * v2), (u3 - q * v3), v1, v2, v3
return u1 % mmodule CryptoMath where
-- |
-- >>> gcd' 55 30
-- 5
gcd' :: Int -> Int -> Int
gcd' a b =
if mod a b == 0
then b
else gcd' b (mod a b)
-- |
-- >>> modInv 5 66
-- Just 53
-- |
-- >>> modInv 6 66
-- Nothing
modInv :: Int -> Int -> Maybe Int
modInv a m
| 1 == g = Just (mkPos i)
| otherwise = Nothing
where
(i, _, g) = gcdExt a m
mkPos x
| x < 0 = x + m
| otherwise = x
-- Extended Euclidean algorithm.
-- Given non-negative a and b, return x, y and g
-- such that ax + by = g, where g = gcd(a,b).
-- Note that x or y may be negative.
gcdExt :: Int -> Int -> (Int, Int, Int)
gcdExt a 0 = (1, 0, a)
gcdExt a b =
let (q, r) = quotRem a b
(s, t, g) = gcdExt b r
in (t, s - q * t, g)https://en.wikipedia.org/wiki/Greatest_common_divisor
A prime number (or a prime) is:
a natural number greater than 1,
that cannot be formed by multiplying two smaller natural numbers.
A composite number, is (the three below are all
equivalent):
a natural number greater than 1 that is not prime.
a positive integer that can be formed by multiplying two smaller
positive integers.
a positive integer that has at least one divisor other than 1 and
itself.

Reminder:
https://en.wikipedia.org/wiki/Integer_factorization
In number theory, integer factorization is the
decomposition of a composite number,
into a product of smaller integers.
If these smaller integers are further restricted to be factored until
they are prime numbers,
then the process is called prime factorization or
prime decomposition.
Factors of 10:
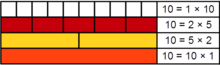
This image demonstrates the prime decomposition of
864:
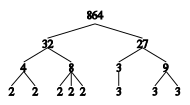
A shorthand way of writing the resulting prime factors is 25
× 33
Preview problem:
When the numbers are sufficiently large,
no efficient integer factorization algorithm is
known,
other than quantum and memristive solutions that do not scale to
factoring large primes… yet.
https://en.wikipedia.org/wiki/Integer_factorization_records
More to come later.
Mention:
This may be the single biggest practical problem in all of computer
science and mathematics today!!
Discussion questions:
If you solved this problem efficiently,
what could you do with the solution?
What would you do?
Do you think you’d live to tell the story if you tried to sell it or use
it,
rather than widely give it away?
../../ComputationalThinking/Content/Recursion.html#greatest-common-divisor-gcd
The greatest common divisor (gcd) of two or more integers,
which are not all zero,
is the largest positive integer that divides each of the integers
evenly.
For example, the gcd of 8 and 12 is 4, written as:
\(gcd(8, 12) = 4\)
An a-by-b rectangle can be covered with square tiles,
of side length c,
only if c is a common divisor of a and
b.

A 24-by-60 rectangle is covered with ten 12-by-12 square tiles,
where 12 is the GCD of 24 and 60.
Greatest common divisors can, in principle,
be computed by determining the prime factorizations of two
numbers,
a and b, and comparing the factors of a and b.
For example,
to compute gcd(18, 84), we find the prime factorizations
18 = 2 * 32 and
84 = 22 * 3 * 7
and the “overlap” of the two expressions is 2 * 3;
so gcd(18, 84) = 6
In practice, this method is only feasible for small numbers.
Computing prime factorizations in general takes faaaaar tooooo
long,
to be an an efficient algorithm to find the CGD.
There are better ways to find the GCD below.
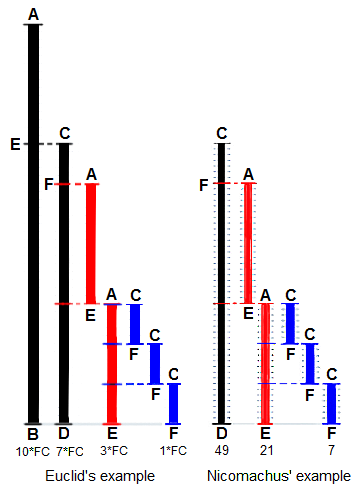
https://en.wikipedia.org/wiki/Euclidean_algorithm
The Euclidean algorithm, or Euclid’s algorithm,
is an efficient method for computing the greatest common divisor (GCD)
of two numbers,
the largest number that divides both of them without leaving a
remainder.
For any non-negative integer a, and any positive integer
b,
gcd(a, b) = gcd(b, a mod b)
V1
function gcd(a, b)
while b ≠ 0
t := b;
b := a mod b;
a := t;
return a;V2
function gcd(a, b)
while a ≠ b
if a > b
a := a − b;
else
b := b − a;
return a;V3
function gcd(a, b)
if b = 0
return a;
else
return gcd(b, a mod b);Check out cryptomath.py for iterative python
version:
AffineCipher/cryptomath.py
# Cryptomath Module
# https://www.nostarch.com/crackingcodes (BSD Licensed)
from typing import Optional
def gcd(a: int, b: int) -> int:
"""
Euclid's Algorithm
Return the Greatest Common Divisor of a and b
"""
while a != 0:
a, b = b % a, a
return b
def findModInverse(a: int, m: int) -> Optional[int]:
# Return the modular inverse of a % m, which is
# the number x such that a*x % m = 1
if gcd(a, m) != 1:
# Ah dynamic typing!
return None
# No single mod inverse exists if a & m aren't relatively prime.
# Calculate using the Extended Euclidean Algorithm:
u1, u2, u3 = 1, 0, a
v1, v2, v3 = 0, 1, m
while v3 != 0:
# Note that // is the integer division operator
q = u3 // v3
v1, v2, v3, u1, u2, u3 = (u1 - q * v1), (u2 - q * v2), (u3 - q * v3), v1, v2, v3
return u1 % mRecursive python version I included for fun:
AffineCipher/gcdRec.py
module CryptoMath where
-- |
-- >>> gcd' 55 30
-- 5
gcd' :: Int -> Int -> Int
gcd' a b =
if mod a b == 0
then b
else gcd' b (mod a b)
-- |
-- >>> modInv 5 66
-- Just 53
-- |
-- >>> modInv 6 66
-- Nothing
modInv :: Int -> Int -> Maybe Int
modInv a m
| 1 == g = Just (mkPos i)
| otherwise = Nothing
where
(i, _, g) = gcdExt a m
mkPos x
| x < 0 = x + m
| otherwise = x
-- Extended Euclidean algorithm.
-- Given non-negative a and b, return x, y and g
-- such that ax + by = g, where g = gcd(a,b).
-- Note that x or y may be negative.
gcdExt :: Int -> Int -> (Int, Int, Int)
gcdExt a 0 = (1, 0, a)
gcdExt a b =
let (q, r) = quotRem a b
(s, t, g) = gcdExt b r
in (t, s - q * t, g)Example operation of gcd() above:

Ask about the complexity of the Euclidean:
For each repetition, by what range does the remaining value to be
computed decrease by?
How do the complexities of the above two algorithms compare?
Can these algorithms handle very large numbers?
https://en.wikipedia.org/wiki/co-prime_integers
Some more number theory:
Two integers a and b are defined to be relatively
prime
(a.k.a., mutually prime or co-prime)
if the only positive integer (factor) that divides both of them is
1.
Consequently, any prime number that divides one does not divide the
other.
This is equivalent to their greatest common divisor (gcd) being 1.
Notes:
Numbers don’t actually have to be prime numbers to be relatively prime
to each other.
All prime numbers are necessarily relatively prime with every other
number, by definition.
Like before, number the symbol set:

Multiply the index of the plaintext letter by the key,
to get the index of the ciphertext letter.
For example, if you encrypted the letter E with the key 3,
then you would find E’s index (4) and multiply it by the key (3),
to get the index of the encrypted letter (4 × 3 = 12),
which would be the letter M.
Ask:
Is that enough?
What about wrap-around?
With a symbol set size of 66,
to encrypt the symbol F with key 17,
multiply its index 5, by the key of 17,
and mod the result by 66,
to handle the wraparound of the 66-symbol set.
The result of (5 × 17) mod 66 is 19,
and 19 corresponds to the symbol T.
So F encrypts to T, in the multiplicative cipher with key 17.
Further, you can’t just use any number for the multiplicative
cipher’s key.
For example, if you chose the key 11,
here’s the plaintext-ciphertext mapping you would end up with:
Plaintext (below)
'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz1234567890 !?.'
'ALWhs4ALWhs4ALWhs4ALWhs4ALWhs4ALWhs4ALWhs4ALWhs4ALWhs4ALWhs4ALWhs4'Ciphertext (above)
Hint:
The row-comparison above must be viewed in mono-spaced (equal width)
font to work.
Ask:
What is the problem?
Notice that this key doesn’t work,
because the symbols A, G, and M all encrypt to the same letter, A.
When you encounter an A in the ciphertext,
and want to decrypt to the plaintext,
you wouldn’t know which symbol it decrypts to.
In the multiplicative cipher,
the key and the size of the symbol set must be relatively prime to each
other!
For example, the numbers num1 and num2 are
relatively prime (co-prime) if
gcd(num1, num2) == 1,
where for this algorithm, num1 is the key and
num2 is the size of the symbol set.
Conclusion:
The multiplicative key (the multiplier) and symbol set size (the mod)
must be co-prime.
Ask:
How do we guarantee that the key and symbol set are relatively prime
(co-prime)?
What algorithm can we use to test this?
Can we select a symbol set size (i.e., modulus),
such that any key will work, and if so, how?
Multiply index of the ciphertext character by the
multiplicative inverse of the key,
mod the symbol set size,
to get back the index of the plaintext character.
The encryption key can be anything you choose,
as long as it’s relatively prime to the size of the symbol set,
which in the example below case is 66.
If you choose the key 53 for encrypting with the multiplicative
cipher,
the decryption key is the modular inverse of 53 mod 66:
If you have your encryption key,
and want to find your decryption key (mod inverse of 53),
then you could use brute force,
starting at 1 (0 can’t be a mod inverse):
1 isn’t the modular inverse of 53 mod 66, because (53 * 1) % 66 =
53
2 isn’t the modular inverse of 53 mod 66, because (53 * 2) % 66 =
40
3 isn’t the modular inverse of 53 mod 66, because (53 * 3) % 66 =
27
4 isn’t the modular inverse of 53 mod 66, because (53 * 4) % 66 =
14
5 is the modular inverse of 53 mod 66, because (53 * 5) % 66 = 1
Because 5 is the modular inverse of 53 mod 66,
you know that the multiplicative cipher decryption key is thus 5.
To decrypt a ciphertext letter,
multiply that letter’s number by 5 and then mod 66.
Using the 66-character symbol set,
let’s encrypt and decrypt the word “Cat” using the key 53.
To encrypt, we multiply by the index of each plaintext letter by 53 % 66
‘C’
C is at index 2, and 2 * 53 is 106,
which is larger than the symbol set size,
so we mod 106 by 66, and the result is 40.
The character at index 40 in the symbol set is ‘o’,
so the symbol C encrypts to o.
‘a’
The string ‘a’ is at index 26 in the symbol set,
and 26 * 53 % 66 is 58,
which is the index of ‘7’.
So the symbol a encrypts to 7.
‘t’
The string ‘t’ is at index 45,
and 45 * 53 % 66 is 9,
which is the index of ‘J’.
Therefore, the word Cat encrypts to
o7J.
To decrypt,
we multiply the index of the ciphertext letter by the modular inverse of
53 % 66,
which is 5.
The symbol o is at index 40,
and 40 * 5 % 66 is 2,
which is the index of ‘C’.
The symbol 7 is at index 58,
and 58 * 5 % 66 is 26,
which is the index of ‘a’.
The symbol J is at index 9,
and 9 * 5 % 66 is 45,
which is the index of ‘t’.
The ciphertext o7J decrypts to
Cat,
which is the original plaintext, just as expected.
Multiplying a number times 1 is what?
RSA will employ the same principle,
for a more advanced trick!
++++++++++++++++++++++++++++
Cahoot_AffineCipher-Keyspace
P: \(\mathbb{Z}_{26} =
\{0, 1, 2, \ldots, 25 \}\)
(or other symbol set size)
C: \(\mathbb{Z}_{26} =
\{0, 1, 2, \ldots, 25 \}\)
(or other symbol set size)
Ke: \(\mathbb{Z}_{?} = ?\)
(Ask, as a function of symbol set size?)
Kd: modular multiplicative inverse of
Ke mod symbol set size (domain of P and C)
(same as Ke?)
E: the encryption function
\(E(x, k) = x * k_{e} \mod 26\)
D: the decryption function
\(D(y, k) = y * k_{d} \mod 26\)
At first glance, it seems like Key A could be as large as you want it
to be,
as long as it’s relatively prime to the symbol set size.
Therefore, you might think that the multiplicative cipher has an
infinite number of keys,
and cannot be brute-forced!
Ask:
Does it wrap around to produce repetitive encryption like Caesar’s?
Conclusion:
Due do the requirement of the key and symbol set size being
co-prime,
the multiplicative cipher has only 20 different keys for a set of 66
symbols,
even fewer than the Caesar cipher!
++++++++++++++++++++++++++++
Cahoot_AffineCipher-RelPrime
https://en.wikipedia.org/wiki/Affine_cipher
One downside to using the multiplicative cipher is that the letter A
always maps to the letter A.
The reason is that A’s number is 0,
and 0 multiplied by anything will always be 0.
You can fix this issue by adding a second key,
to perform a Caesar cipher encryption,
after the multiplicative cipher’s multiplication and modding is
done.
This extra step changes the multiplicative cipher into the affine
cipher.
It also enlarges the keyspace!
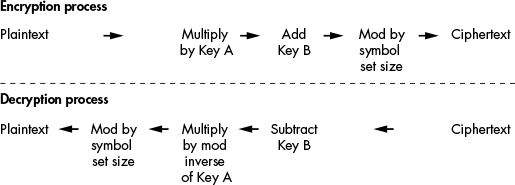
The affine cipher is a two-part process:
The affine cipher has two keys: Key A and Key
B.
Key A is the integer you use to multiply the letter’s number.
After you multiply the plaintext by Key A,
you add Key B to the product.
Then you mod the sum by 66 (or other symbol set size),
as you did in the original Caesar cipher.
Does this mean the affine cipher has 66 times as many possible
keys,
when compared to the multiplicative cipher?
It also ensures that the letter A doesn’t always encrypt to itself.
Return to modular multiplicative inverse above.
P: \(\mathbb{Z}_{26} =
\{0, 1, 2, \ldots, 25 \}\)
(or symbol set size)
C: \(\mathbb{Z}_{26} =
\{0, 1, 2, \ldots, 25 \}\)
(or symbol set size)
\(K_{a_e}\): \(\mathbb{Z}_{?} = ?\)
(Ask, as a function of symbol set size)
\(K_{a_d}\):
modular multiplicative inverse of Kae mod symbol set size
(domain of P and C)
Kb: \(\mathbb{Z}_{26} = \{0, 1, 2, \ldots, 25 \}\)
E: the encryption function
\(E(x, k_a, k_b) = x * k_{a_e} + k_b \mod
26\)
D: the decryption function
\(D(y, k_a, k_b) = (y - k_b) * k_{a_d} \mod
26\)
Code
Step through: $ pudb3 affineCipher.py
AffineCipher/affineCipher.py
#!/usr/bin/python3
# -*- coding: utf-8 -*-
# Affine Cipher
# https://www.nostarch.com/crackingcodes (BSD Licensed)
import sys, cryptomath, random
from typing import Tuple
SYMBOLS = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz1234567890 !?."
def main() -> None:
myMessage = "A computer would deserve to be called intelligent if it could deceive a human into believing that it was human. -Alan Turing"
myKey = 2894
myMode = "encrypt" # Set to either 'encrypt' or 'decrypt'.
if myMode == "encrypt":
translated = encryptMessage(myKey, myMessage)
elif myMode == "decrypt":
translated = decryptMessage(myKey, myMessage)
print(f"Key: {getKeyParts(myKey)}")
print("%sed text:" % (myMode.title()))
print(translated)
print("Full %sed text copied to clipboard." % (myMode))
def getKeyParts(key: int) -> Tuple[int, int]:
"""
Splits a single integer key into two integers for Key A and Key B.
The key to split is passed to the key parameter.
Key A is calculated by using integer division,
to divide key by len(SYMBOLS), the size of the symbol set.
Integer division (//) returns the quotient without a remainder.
The mod operator (%) on line 26 calculates the remainder,
which we’ll use for Key B.
For example,
with 2894 as the key parameter and a SYMBOLS string of 66 characters,
Key A would be 2894 // 66 = 43 and Key B would be 2894 % 66 = 56.
To combine Key A and Key B back into a single key,
multiply Key A by the size of the symbol set and add Key B to the product:
(43 * 66) + 56 evaluates to 2894, which is the integer key we started with.
This is not required, and is just a cute way to store 2 keys in one.
"""
keyA = key // len(SYMBOLS)
keyB = key % len(SYMBOLS)
return (keyA, keyB)
def checkKeys(keyA: int, keyB: int, mode: str) -> None:
if keyA == 1 and mode == "encrypt":
sys.exit("Cipher is weak if key A is 1. Choose a different key.")
if keyB == 0 and mode == "encrypt":
sys.exit("Cipher is weak if key B is 0. Choose a different key.")
if keyA < 0 or keyB < 0 or keyB > len(SYMBOLS) - 1:
sys.exit(
"Key A must be greater than 0 and Key B must be between 0 and %s."
% (len(SYMBOLS) - 1)
)
if cryptomath.gcd(keyA, len(SYMBOLS)) != 1:
sys.exit(
"Key A (%s) and the symbol set size (%s) are not relatively prime."
"Choose a different key." % (keyA, len(SYMBOLS))
)
def encryptMessage(key: int, message: str) -> str:
keyA, keyB = getKeyParts(key)
checkKeys(keyA, keyB, "encrypt")
ciphertext = ""
for symbol in message:
if symbol in SYMBOLS:
# Encrypt the symbol:
symbolIndex = SYMBOLS.find(symbol)
ciphertext += SYMBOLS[(symbolIndex * keyA + keyB) % len(SYMBOLS)]
else:
ciphertext += symbol # Append the symbol without encrypting.
return ciphertext
def decryptMessage(key: int, message: str) -> str:
keyA, keyB = getKeyParts(key)
checkKeys(keyA, keyB, "decrypt")
plaintext = ""
modInverseOfKeyA = cryptomath.findModInverse(keyA, len(SYMBOLS))
# just for sane typing on the findModInverse Optional[int]
if modInverseOfKeyA:
for symbol in message:
if symbol in SYMBOLS:
# Decrypt the symbol:
symbolIndex = SYMBOLS.find(symbol)
plaintext += SYMBOLS[
(symbolIndex - keyB) * modInverseOfKeyA % len(SYMBOLS)
]
else:
plaintext += symbol # Append the symbol without decrypting.
return plaintext
def getRandomKey() -> int:
while True:
keyA = random.randint(2, len(SYMBOLS))
keyB = random.randint(2, len(SYMBOLS))
if cryptomath.gcd(keyA, len(SYMBOLS)) == 1:
return keyA * len(SYMBOLS) + keyB
# If affineCipher.py is run (instead of imported as a module) call
# the main() function.
if __name__ == "__main__":
main()Haskell version:
AffineCipher/AffineCipher.hs
#!/usr/bin/runghc
module AffineCipher (encryptString, decryptString, m) where
import CryptoMath
import Data.List
import Data.Maybe
import Test.QuickCheck
symbolSet :: String
symbolSet = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz1234567890 !?."
m :: Int
m = length symbolSet
-- |
-- >>> encodeChar 'A'
-- Just 0
encodeChar :: Char -> Maybe Int
encodeChar symbol = elemIndex symbol symbolSet
-- |
-- >>> decodeChar 0
-- 'A'
decodeChar :: Int -> Char
decodeChar index = symbolSet !! index
-- |
-- >>> encKeyPoint 5 2 4
-- 22
-- |
-- >>> encKeyPoint 5 2 65
-- 63
encKeyPoint :: Int -> Int -> Int -> Int
encKeyPoint keyA keyB codePoint = mod (codePoint * keyA + keyB) m
-- |
-- >>> decKeyPoint 5 2 22
-- 4
-- |
-- >>> decKeyPoint 5 2 63
-- 65
decKeyPoint :: Int -> Int -> Int -> Int
decKeyPoint keyA keyB codePoint = mod ((codePoint - keyB) * fromJust (modInv keyA m)) m
-- fromJust is reasonable above, because we assume valid keys were selected for encryption.
-- |
-- >>> encryptChar 5 2 'A'
-- 'C'
encryptChar :: Int -> Int -> Char -> Char
encryptChar keyA keyB c = case encodeChar c of
Nothing -> c
Just codePoint -> decodeChar (encKeyPoint keyA keyB codePoint)
-- |
-- >>> decryptChar 5 2 'B'
-- 'N'
decryptChar :: Int -> Int -> Char -> Char
decryptChar keyA keyB c = case encodeChar c of
Nothing -> c
Just codePoint -> decodeChar (decKeyPoint keyA keyB codePoint)
-- |
-- >>> encryptString 5 2 "zed."
-- "8UP!"
encryptString :: Int -> Int -> String -> String
encryptString keyA keyB = map (encryptChar keyA keyB)
-- |
-- >>> decryptString 5 2 "8UP!"
-- "zed."
decryptString :: Int -> Int -> String -> String
decryptString keyA keyB = map (decryptChar keyA keyB)
main :: IO ()
main = do
let message = "A computer would deserve to be called intelligent if it could deceive a human into believing that it was human. -Alan Turing"
let keyA = 43
let keyB = 56
putStrLn "Your encrypted message is:"
putStrLn (encryptString keyA keyB message)
putStrLn "Your decrypted ciphertext is:"
putStrLn (decryptString keyA keyB (encryptString keyA keyB message))How do ranges of values for key a and key b interact?
How to loop across all keys?
How might we test that?
Check out $ pudb3 affineKeyTest.py
AffineCipher/affineKeyTest.py
#!/usr/bin/python3
# -*- coding: utf-8 -*-
# This program demonstrates that the keyspace of the affine cipher is limited,
# to less than len(SYMBOLS) ^ 2.
import affineCipher
import cryptomath
message: str = "Make things as simple as possible, but not simpler."
for keyA in range(2, 80):
key = keyA * len(affineCipher.SYMBOLS) + 1
if cryptomath.gcd(keyA, len(affineCipher.SYMBOLS)) == 1:
print(keyA, affineCipher.encryptMessage(key, message))And a Haskell version:
AffineCipher/AffineKeyTest.hs
import AffineCipher
-- |
-- >>> keySpace
-- 1254
keySpace = length [(keyA, keyB) | keyA <- [2 .. m], gcd keyA m == 1, keyB <- [1 .. m]]Assuming a symbol set size of 66:
When you multiply 66 possible Key A values by 66 possible Key B
values,
the result is 4356 possible combinations.
Then when you subtract the integers that can’t be used for Key
A,
because they’re not relatively prime with 66,
the total number of possible key combinations for the affine cipher
drops to 1254,
which is our best yet!
++++++++++++++++++++++++++
Cahoot_AffineCipher-Euclid
Code
Step through $ pudb3 affineHacker.py
AffineCipher/affineHacker.py
#!/usr/bin/python3
# -*- coding: utf-8 -*-
# Affine Cipher Hacker
# https://www.nostarch.com/crackingcodes (BSD Licensed)
import affineCipher, detectEnglish, cryptomath
from typing import Optional
SILENT_MODE = False
def main() -> None:
# You might want to copy & paste this text from the source code at
# https://www.nostarch.com/crackingcodes/affineHacker.py
myMessage = """"5QG9ol3La6QI93!xQxaia6faQL9QdaQG1!!axQARLa!!AuaRLQADQALQG93!xQxaGaAfaQ1QX3o1RQARL9Qda!AafARuQLX1LQALQI1iQX3o1RN"Q-5!1RQP36ARu"""
hackedMessage = hackAffine(myMessage)
if hackedMessage != None:
# The plaintext is displayed on the screen. For the convenience of
# the user, we copy the text of the code to the clipboard.
print("Copying hacked message to clipboard:")
print(hackedMessage)
else:
print("Failed to hack encryption.")
def hackAffine(message: str) -> Optional[str]:
print("Hacking...")
# Python programs can be stopped at any time by pressing Ctrl-C (on
# Windows) or Ctrl-D (on Mac and Linux)
print("(Press Ctrl-C or Ctrl-D to quit at any time.)")
# Brute-force by looping through every possible key
for key in range(len(affineCipher.SYMBOLS) ** 2):
keyA = affineCipher.getKeyParts(key)[0]
if cryptomath.gcd(keyA, len(affineCipher.SYMBOLS)) != 1:
continue
decryptedText = affineCipher.decryptMessage(key, message)
if not SILENT_MODE:
print("Tried Key %s... (%s)" % (key, decryptedText[:40]))
if detectEnglish.isEnglish(decryptedText):
# Check with the user if the decrypted key has been found.
print()
print("Possible encryption hack:")
print("Key: %s" % (key))
print("Decrypted message: " + decryptedText[:200])
print()
print("Enter D if done, anything else to continue hacking:")
response = input("> ")
if response.strip().upper().startswith("D"):
return decryptedText
return None
# If affineHacker.py is run (instead of imported as a module)
# call the main() function.
if __name__ == "__main__":
main()Haskell version:
AffineCipher/AffineHacker.hs
#!/usr/bin/runghc
import AffineCipher
import Data.HashSet (HashSet)
import Data.List
import DetectEnglish
affineHacker :: HashSet String -> Float -> String -> [((Int, Int), String)]
affineHacker wordList threshold message =
[ ((keyA, keyB), decryptString keyA keyB message)
| keyA <- [2 .. m],
gcd keyA m == 1,
keyB <- [1 .. m],
isEnglish wordList threshold (decryptString keyA keyB message)
]
main :: IO ()
main = do
let message = "A computer would deserve to be called intelligent if it could deceive a human into believing that it was human. -Alan Turing"
let keyA = 43
let keyB = 56
putStrLn "Your encrypted message is:"
putStrLn (encryptString keyA keyB message)
hashDict <- importDictionary
putStrLn "Your cracked ciphertext is:"
print (affineHacker hashDict 0.2 (encryptString keyA keyB message))