“The mantra of any good security engineer is:
Security is a not a product, but a process.
It’s more than designing strong cryptography into a
system;
it’s designing the entire system such that all security
measures,
including cryptography, work together.”
- Bruce Schneier
https://en.wikipedia.org/wiki/Bruce_Schneier
https://www.schneier.com/
Discussion question:
Which parts of a computer system matter the most?
A system have high and low level parts.
Do the high or low level parts matter more?
Why?
Does any pattern always hold?
http://inventwithpython.com/cracking/ Chapter 24
Very good tutorial on RSA; read it!
http://doctrina.org/How-RSA-Works-With-Examples.html
Very good tutorial on RSA; read it!
http://doctrina.org/Why-RSA-Works-Three-Fundamental-Questions-Answered.html
document.querySelector('video').playbackRate = 1.2Classification of Encryption Schemes
A significant distinction.
Also referred to as private key encryption.
There is one private or secret key, which is generally shared between
two parties.
Both encryption and decryption use the same key, and a similar
process.
Key agreement and exchange can be a very challenging problem.
Relies on making a big mess of the data, using the pre-exchanged key,
reversibly.
Generally computationally efficient to encrypt and decrypt (fast).
Examples of “modern” symmetric algorithms:
AES, DES, 3DES
Faster than asymmetric.
It is also referred as public key encryption.
It has two keys: one public and one private.
The encryption operation uses only the public key,
which is known to everyone.
The decryption operation uses only the private key,
which is known to one person.
Modern innovation (newer algorithms).
Relies on math tricks (one way functions).
Moderately computationally expensive,
both in key-generation and in encryption and decryption.
Examples of “modern” asymmetric algorithms: RSA, DSA, ElGamal,
NTRU.
Slower than asymmetric.
+++++++++++++++++++++
Cahoot-08.1
A computationally secure encryption scheme,
assumes the adversary has limited computing
power.
The adversary can be assumed to solve polynomially-bounded
problems,
but not to solve computationally infeasible NP-Complete, NP-hard, etc.
problems
Almost all practical encryption schemes,
e.g., AES and RSA, are computationally secure.
An information-theoretically secure encryption scheme,
assumes the adversary has unlimited computing
power.
The adversary can be assumed to solve any computational problems
NP-Complete and NP-hard could hypothetically be efficiently
solved,
and the scheme would still offer perfect security
Unconditional or perfect security.
One-time pad is information theoretically secure.
There are variants of the OTP,
but it’s the only one that fits this criteria.
Proposed by Diffie and Hellman in 1976 (quite recently!)
Based on mathematical one-way functions.
Q: What do we mean by one-way?
A: Those operations where the best algorithm to reverse them is a form
of brute force.
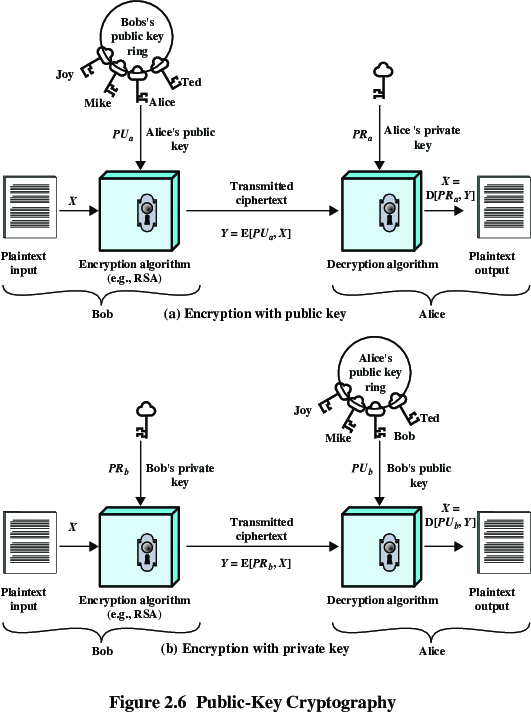
Asymmetric schemes use two separate keys:
public key
private key
Public key is made public for others to use.
Plaintext: Readable message or data that is fed into
the algorithm as input
Encryption algorithm: Performs transformations on the
plaintext
Public and private key: Pair of keys, one for
encryption, one for decryption
Ciphertext: Scrambled message produced as output
Decryption key: Produces the original plaintext.
Q: Why seemingly redundant definition?
A: either can decrypt or encrypt
Decryption algorithm: Accepts the ciphertext and the
matching key, and produces the original plaintext.
Should be:
Computationally easy for a party B to generate a pair,
(public key PUb, private key PRb).
Computationally easy for a sender A,
knowing the public key and the message to be encrypted, M,
to generate the corresponding ciphertext:
C = E(PUb , M)
Computationally easy for the receiver B to decrypt the resulting
ciphertext,
using the private key to recover the original message:
M = D(PRb ,C) = D[PRb, E(PUb, M)]
Computationally infeasible for an opponent,
knowing the public key, PUb,
to determine the private key, PRb
Computationally infeasible for an opponent,
knowing the public key, PUb, and a ciphertext, C,
to recover the original message, M.
Optionally, either of the two related keys can be used for
encryption,
with the other used for decryption.
M = D[PUb, E(PRb, M)] = D[PRb,
E(PUb, M)]
This is a neat feature, that you will see exists in RSA!
Meet Alice and Bob (and sometimes evil Eve)!
https://en.wikipedia.org/wiki/Alice_and_Bob
http://cryptocouple.com/
Each user generates pair of related keys, public and private.
ob encrypts a message using Alice’s
public key.
Alice decrypts messages using her private key;
no other recipient can decrypt the message,
because only Alice knows Alice’s private key.
Go over this carefully:

Bottom half: switch key roles
User encrypts data using his or her own
private key.
Anyone who knows the corresponding public key will be
able to decrypt the message.
Used for authenticating both:
source identity, and data integrity.
Created by encrypting hash code with private key.
Does not provide confidentiality,
even in the case of complete encryption.
Message is safe from alteration, but not eavesdropping.
Encryption is provided independently.

RSA (Rivest, Shamir, Adleman)
Developed in 1977.
This is the most widely accepted and implemented approach to public-key
encryption.
Block cipher in which the plaintext and ciphertext are integers between
0 and n-1 for some n.
Diffie-Hellman key exchange algorithm
Enables two users to securely reach agreement about a shared
secret,
that can be used as a secret key for subsequent symmetric encryption of
messages.
Most widely accepted and implemented approach to key exchange.
Limited to the exchange of the keys, with no direct encryption.
Digital Signature Standard (DSS)
Provides only a digital signature function with SHA-1.
Cannot be used for encryption or key exchange.
Elliptic curve cryptography (ECC)
Security like RSA, but with much smaller keys for similar security.
Read Chapter 9 and all Appendices:
https://github.com/crypto101/crypto101.github.io/raw/master/Crypto101.pdf
https://en.wikipedia.org/wiki/RSA_(cryptosystem)
https://simple.wikipedia.org/wiki/RSA_algorithm
Video series detailing the algorithm:
https://www.khanacademy.org/computing/computer-science/cryptography/modern-crypt/v/intro-to-rsa-encryption
Publically invented by Rivest, Shamir, and Adleman of MIT in
1977.
For a time, it was the best known, and widely used public-key
algorithm.
Uses exponentiation of integers, modulo some prime.
For a moment, let’s see the magic:
How?
Key generation involves multiple steps of repeated generate and
test.
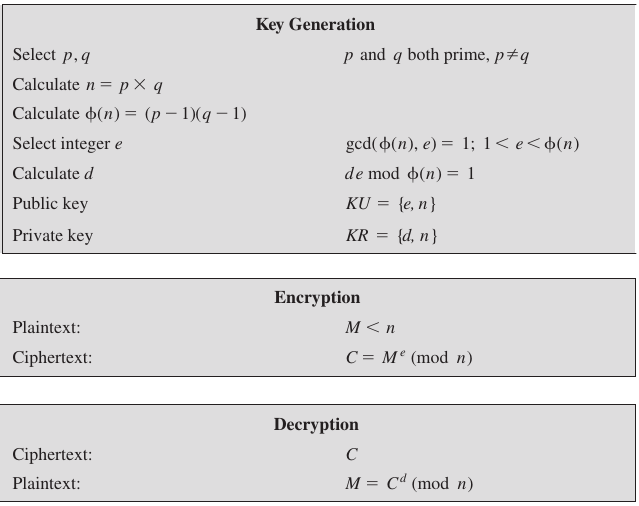
Each key in the public key scheme is made of two numbers.
The public key will be two numbers, n and e.
The private key will be two numbers, n and d.
The steps to create these numbers follow:
Generate many random numbers,
until you find two that are distinct, very very large, and prime:
p and q
Multiply these two numbers,
p x q = n (n will then be the modulus for encryption).
Also, multiply these two numbers minus 1,
(p - 1) × (q - 1)
to get a number called \(\phi(n)\) (the
modulus for key generation).
Generate many more random numbers,
until you find another number, which we will call e,
which is relatively prime to n.
This is part of the public key.
Calculate the modular inverse of e, which we’ll call d.
This is part of the private key.
Side note:
In practice, e is often just chosen as 65537, or some other fixed
value…
Notice that the modulus, n, is used in both keys.
By convention, the d number must be kept secret,
as only it can decrypt messages encrypted to e,
which is pubic information.
More formally, generate
numbers p and q, where
where p and q are very very large primes, with roughly similar sizes,
and
n = p * q
The size of p or q needs to be at least 2,048
bits,
though 4096 is a practical current upper limit in most
implementations.
Plaintext space:
Zn
Ciphertext space:
Zn
Public key:
n, e, where,
e is an integer relatively prime to \(\phi(n)\)
Private key:
d where
\(ed \equiv 1 \mod \phi(n)\)
Each done in sequence, in either direction, will cancel the other out!
Encryption: E(x, n, e) = xe mod n
Decryption: D(c, n, d) = cd mod n
= xed mod n
= x1
The above formulation is an over-simplification of the real
proof,
but illustrates a key theoretical point.
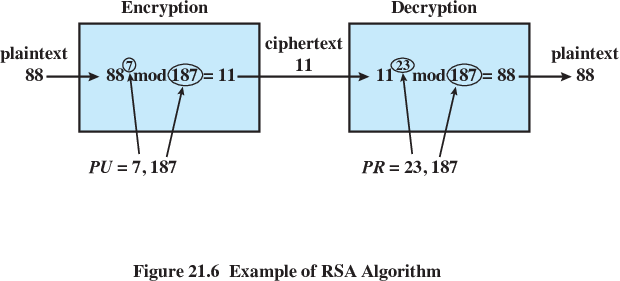
Iteratively, pick two primes:
p = 11
q = 17
Multiply (p - 1) × (q - 1):
n = 11 * 17 = 187
\(\phi(n)\) = 10 * 16 = 160
Iteratively with GCD Euclidean,
pick a relative prime to \(\phi(n)\):
e = 3
Using Extended Euclidean,
compute the inverse of e mod \(\phi(n)\):
d = 107
Write your hypothetical message:
Plaintext character encoded here as x = 10
Encrypt, producing ciphertext:
c = 103 mod 187 = 65
To decrypt C,
compute: D(c, e):
65107 mod 187 = 10
Some are public.
Some are secret.
n - the modulus
e - the public exponent
c - the cipher text
p - the prime factor of n
q - the other prime factor of n
\(\phi(n)\) - Euler’s totient of
n
d - the private exponent
+++++++++++++++++++++
Cahoot-08.2
Brute force:
Involves trying all possible private keys.
Mathematical attacks:
There are several approaches,
all equivalent in effort to factoring the product of two primes.
Timing attacks:
These extract statistics based on on analyzing the running time of the
decryption algorithm.
Chosen cipehrtext attacks:
This type of attack exploits properties of the RSA algorithm,
given some oracle,
which can produce arbitrary encrypted data for the attacker.
The easiest way we know how to break RSA is to factor n back into p *
q,
which is a prime factorization…
After that, given p and q, the attacker could just repeat the analytical
process,
that the legitimate owner of the key does during key generation,
in order to compute the private exponent d.
Fortunately, we don’t have an algorithm that can factor such large
numbers in reasonable time.
Unfortunately, we also haven’t proven it doesn’t exist.
Even more unfortunately, is that there is a theoretical algorithm,
called Shor’s algorithm,
that would be able to factor such a number in reasonable time on a
quantum computer.
There is another memristive solution (non-Turing),
implemented in application-specific hardware,
that can factor primes in polynomial resources (energy).
Right now, quantum and memristive solutions are far from
practical,
but it does appear that, if someone in the future manages to build one
sufficiently large,
that RSA becomes ineffective.
Ask and discuss:
Does this just break RSA, or other algorithms too?
RSA Labs (http://www.rsasecurity.com/rsalabs/) sponsored a challenge to factor some large n:
https://en.wikipedia.org/wiki/RSA_Factoring_Challenge
Progress in Factorization:
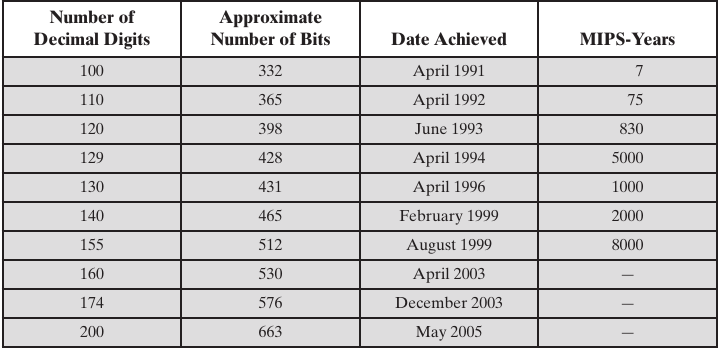
What is a modern size?
How much bigger and better is it?
https://en.wikipedia.org/wiki/Integer_factorization_records
+++++++++++++++++++++
Cahoot-08.3
AsymmetricEncryption/cryptomath.py
AsymmetricEncryption/primeNum.py
#!/usr/bin/python3
# -*- coding: utf-8 -*-
# Prime Number Sieve
# https://www.nostarch.com/crackingcodes/ (BSD Licensed)
import math, random
from typing import List
def isPrimeTrialDiv(num: int) -> bool:
"""
Returns True if num is a prime number, otherwise False.
Uses the trial division algorithm for testing primality.
"""
# All numbers less than 2 are not prime:
if num < 2:
return False
# See if num is divisible by any number up to the square root of num:
for i in range(2, int(math.sqrt(num)) + 1):
if num % i == 0:
return False
return True
def primeSieve(sieveSize: int) -> List[int]:
"""
Returns a list of prime numbers calculated using
the Sieve of Eratosthenes algorithm.
"""
sieve = [True] * sieveSize
sieve[0] = False # Zero and one are not prime numbers.
sieve[1] = False
# Create the sieve:
for i in range(2, int(math.sqrt(sieveSize)) + 1):
pointer = i * 2
while pointer < sieveSize:
sieve[pointer] = False
pointer += i
# Compile the list of primes:
primes = []
for i in range(sieveSize):
if sieve[i] == True:
primes.append(i)
return primes
def rabinMiller(num: int) -> bool:
"""Returns True if num is a prime number."""
if num % 2 == 0 or num < 2:
return False # Rabin-Miller doesn't work on even integers.
if num == 3:
return True
s = num - 1
t = 0
while s % 2 == 0:
# Keep halving s until it is odd (and use t
# to count how many times we halve s):
s = s // 2
t += 1
for trials in range(5): # Try to falsify num's primality 5 times.
a = random.randrange(2, num - 1)
v = pow(a, s, num)
if v != 1: # (This test does not apply if v is 1.)
i = 0
while v != (num - 1):
if i == t - 1:
return False
else:
i = i + 1
v = (v**2) % num
return True
# Most of the time we can quickly determine if num is not prime
# by dividing by the first few dozen prime numbers. This is quicker
# than rabinMiller(), but does not detect all composites.
LOW_PRIMES = primeSieve(100)
def isPrime(num: int) -> bool:
"""
Return True if num is a prime number. This function does a quicker
prime number check before calling rabinMiller().
"""
if num < 2:
return False # 0, 1, and negative numbers are not prime.
# See if any of the low prime numbers can divide num:
for prime in LOW_PRIMES:
if num == prime:
return True
if num % prime == 0:
return False
# If all else fails, call rabinMiller() to determine if num is a prime:
return rabinMiller(num)
def generateLargePrime(keysize: int = 1024) -> int:
"""Return a random prime number that is keysize bits in size."""
while True:
num = random.randrange(2 ** (keysize - 1), 2 ** (keysize))
if isPrime(num):
return numAsymmetricEncryption/makeRSAKeys.py
#!/usr/bin/python3
# -*- coding: utf-8 -*-
# Public Key Generator
# https://www.nostarch.com/crackingcodes/ (BSD Licensed)
import random, sys, os, primeNum, cryptomath
from typing import Tuple
def main() -> None:
# Create a public/private keypair with 1024 bit keys:
print("Making key files...")
makeKeyFiles("al_sweigart", 1024)
print("Key files made.")
def generateKey(keySize: int) -> Tuple[Tuple[int, int], Tuple[int, int]]:
# Creates a public/private keys keySize bits in size.
p = 0
q = 0
# Step 1: Create two prime numbers, p and q. Calculate n = p * q.
print("Generating p & q primes...")
while p == q:
p = primeNum.generateLargePrime(keySize)
q = primeNum.generateLargePrime(keySize)
n = p * q
# Step 2: Create a number e that is relatively prime to (p-1)*(q-1):
print("Generating e that is relatively prime to (p-1)*(q-1)...")
phiN = (p - 1) * (q - 1)
while True:
# Keep trying random numbers for e until one is valid:
e = random.randrange(2 ** (keySize - 1), 2 ** (keySize))
if cryptomath.gcd(e, phiN) == 1:
break
# Step 3: Calculate d, the mod inverse of e:
print("Calculating d that is mod inverse of e...")
d = cryptomath.findModInverse(e, phiN)
publicKey = (n, e)
privateKey = (n, d)
print("Public key:", publicKey)
print("Private key:", privateKey)
return (publicKey, privateKey)
def makeKeyFiles(name: str, keySize: int) -> None:
# Creates two files 'x_pubkey.txt' and 'x_privkey.txt' (where x
# is the value in name) with the n,e and d,e integers written in
# them, delimited by a comma.
# Our safety check will prevent us from overwriting our old key files:
if os.path.exists("%s_pubkey.txt" % (name)) or os.path.exists(
"%s_privkey.txt" % (name)
):
sys.exit(
"Files %s_pubkey.txt or %s_privkey.txt already exists! Use a different name, or delete keys and re-run."
% (name, name)
)
publicKey, privateKey = generateKey(keySize)
print(
"\nThe public key is a %s and a %s digit number."
% (len(str(publicKey[0])), len(str(publicKey[1])))
)
print("Writing public key to file %s_pubkey.txt..." % (name))
with open("%s_pubkey.txt" % (name), "w") as fo:
fo.write("%s,%s,%s" % (keySize, publicKey[0], publicKey[1]))
print(
"\nThe private key is a %s and a %s digit number."
% (len(str(publicKey[0])), len(str(publicKey[1])))
)
print("Writing private key to file %s_privkey.txt..." % (name))
with open("%s_privkey.txt" % (name), "w") as fo:
fo.write("%s,%s,%s" % (keySize, privateKey[0], privateKey[1]))
# If makePublicPrivateKeys.py is run (instead of imported as a module),
# call the main() function:
if __name__ == "__main__":
main()AsymmetricEncryption/RSACipher.py
#!/usr/bin/python3
# -*- coding: utf-8 -*-
# Public Key Cipher
# https://www.nostarch.com/crackingcodes/ (BSD Licensed)
import sys, math
from typing import List, Optional, Tuple
# The public and private keys for this program are created by
# the makePublicPrivateKeys.py program.
# This program must be run in the same folder as the key files.
SYMBOLS = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz1234567890 !?."
def main() -> None:
# Runs a test that encrypts a message to a file or decrypts a message from a file.
filename = "encrypted_file.txt" # The file to write to/read from.
# mode = "decrypt" # Set to either 'encrypt' or 'decrypt'.
mode = input("Type 'encrypt' or 'decrypt' and hit enter: ")
if mode == "encrypt":
message = "Journalists belong in the gutter because that is where the ruling classes throw their guilty secrets. Gerald Priestland. The Founding Fathers gave the free press the protection it must have to bare the secrets of government and inform the people. Hugo Black."
pubKeyFilename = "al_sweigart_pubkey.txt"
print("Encrypting and writing to %s..." % (filename))
encryptedText = encryptAndWriteToFile(filename, pubKeyFilename, message)
print("Encrypted text:")
print(encryptedText)
elif mode == "decrypt":
privKeyFilename = "al_sweigart_privkey.txt"
print("Reading from %s and decrypting..." % (filename))
decryptedText = readFromFileAndDecrypt(filename, privKeyFilename)
print("Decrypted text:")
print(decryptedText)
def getBlocksFromText(message: str, blockSize: int) -> List[int]:
# Converts a string message to a list of block integers.
for character in message:
if character not in SYMBOLS:
print("ERROR: The symbol set does not have the character %s" % (character))
sys.exit()
blockInts = []
for blockStart in range(0, len(message), blockSize):
# Calculate the block integer for this block of text:
blockInt = 0
for i in range(blockStart, min(blockStart + blockSize, len(message))):
blockInt += (SYMBOLS.index(message[i])) * (len(SYMBOLS) ** (i % blockSize))
blockInts.append(blockInt)
return blockInts
def getTextFromBlocks(blockInts: List[int], messageLength: int, blockSize: int) -> str:
# Converts a list of block integers to the original message string.
# The original message length is needed to properly convert the last
# block integer.
message: List[str] = []
for blockInt in blockInts:
blockMessage: List[str] = []
for i in range(blockSize - 1, -1, -1):
if len(message) + i < messageLength:
# Decode the message string for the 128 (or whatever
# blockSize is set to) characters from this block integer:
charIndex = blockInt // (len(SYMBOLS) ** i)
blockInt = blockInt % (len(SYMBOLS) ** i)
blockMessage.insert(0, SYMBOLS[charIndex])
message.extend(blockMessage)
return "".join(message)
def encryptMessage(message: str, key: Tuple[int, int], blockSize: int) -> List[int]:
# Converts the message string into a list of block integers, and then
# encrypts each block integer. Pass the PUBLIC key to encrypt.
encryptedBlocks = []
n, e = key
for block in getBlocksFromText(message, blockSize):
# ciphertext = plaintext ^ e mod n
encryptedBlocks.append(pow(block, e, n))
return encryptedBlocks
def decryptMessage(
encryptedBlocks: List[int], messageLength: int, key: Tuple[int, int], blockSize: int
) -> str:
# Decrypts a list of encrypted block ints into the original message
# string. The original message length is required to properly decrypt
# the last block. Be sure to pass the PRIVATE key to decrypt.
decryptedBlocks = []
n, d = key
for block in encryptedBlocks:
# plaintext = ciphertext ^ d mod n
decryptedBlocks.append(pow(block, d, n))
return getTextFromBlocks(decryptedBlocks, messageLength, blockSize)
def readKeyFile(keyFilename: str) -> Tuple[int, int, int]:
# Given the filename of a file that contains a public or private key,
# return the key as a (n,e) or (n,d) tuple value.
with open(keyFilename) as fo:
content = fo.read()
keySize, n, EorD = content.split(",")
return (int(keySize), int(n), int(EorD))
def encryptAndWriteToFile(
messageFilename: str,
keyFilename: str,
message: str,
blockSize: Optional[int] = None,
) -> str:
# Using a key from a key file, encrypt the message and save it to a
# file. Returns the encrypted message string.
keySize, n, e = readKeyFile(keyFilename)
if blockSize is None:
# If blockSize isn't given, set it to the largest size allowed by the key size and symbol set size.
blockSize = int(math.log(2**keySize, len(SYMBOLS)))
# Check that key size is large enough for the block size:
if not (math.log(2**keySize, len(SYMBOLS)) >= blockSize):
sys.exit(
"ERROR: Block size is too large for the key and symbol set size. Did you specify the correct key file and encrypted file?"
)
# Encrypt the message:
encryptedBlocks = encryptMessage(message, (n, e), blockSize)
# Convert the large int values to one string value:
# for i in range(len(encryptedBlocks)):
# encryptedBlocks[i] = str(encryptedBlocks[i])
# encryptedContent = ",".join(encryptedBlocks)
encryptedContent = ",".join(map(str, encryptedBlocks))
# Write out the encrypted string to the output file:
encryptedContent = "%s_%s_%s" % (len(message), blockSize, encryptedContent)
with open(messageFilename, "w") as fo:
fo.write(encryptedContent)
# Also return the encrypted string:
return encryptedContent
def readFromFileAndDecrypt(messageFilename: str, keyFilename: str) -> str:
# Using a key from a key file, read an encrypted message from a file
# and then decrypt it. Returns the decrypted message string.
keySize, n, d = readKeyFile(keyFilename)
# Read in the message length and the encrypted message from the file:
with open(messageFilename) as fo:
content = fo.read()
messageLength_str, blockSize_str, encryptedMessage = content.split("_")
messageLength = int(messageLength_str)
blockSize = int(blockSize_str)
# Check that key size is large enough for the block size:
if not math.log(2**keySize, len(SYMBOLS)) >= blockSize:
sys.exit(
"ERROR: Block size is too large for the key and symbol set size. Did you specify the correct key file and encrypted file?"
)
# Convert the encrypted message into large int values:
encryptedBlocks = []
for block in encryptedMessage.split(","):
encryptedBlocks.append(int(block))
# Decrypt the large int values:
return decryptMessage(encryptedBlocks, messageLength, (n, d), blockSize)
# If publicKeyCipher.py is run (instead of imported as a module) call
# the main() function.
if __name__ == "__main__":
main()Ask:
What line does the encryption?
Hint:
$ python3
>>> help(pow)
pow(x, y, z=None)
Equivalent to x**y (with two arguments)
or x**y % z (with three arguments).
Some types, such as ints,
are able to use a more efficient algorithm,
when invoked using the three argument form.Ask and discuss:
How do you take a string like 'Hello RSA’ to a power??
In order to encrypt text or data,
it must be turned into a number.
A method with blocks is used above.
How the text is turned into a number differs by implementation,
and is conceptually independent of the core RSA algorithm,
though it impacts the security!
AsymmetricEncryption/CryptoMath.hs
{-# LANGUAGE BangPatterns #-}
module CryptoMath where
fastpow :: Integer -> Integer -> Integer -> Integer
fastpow base exp modulo =
let fastpow' b 0 m !r = r
fastpow' b e m r = fastpow' (mod (b * b) m) (div e 2) m (if even e then r else mod (r * b) m)
in fastpow' (mod base modulo) exp modulo 1
-- |
-- >>> gcd' 55 30
-- 5
gcd' :: Integer -> Integer -> Integer
gcd' a b =
if mod a b == 0
then b
else gcd' b (mod a b)
-- |
-- >>> modInv 5 66
-- Just 53
-- |
-- >>> modInv 6 66
-- Nothing
modInv :: Integer -> Integer -> Maybe Integer
modInv a m
| 1 == g = Just (mkPos i)
| otherwise = Nothing
where
(i, _, g) = gcdExt a m
mkPos x
| x < 0 = x + m
| otherwise = x
-- Extended Euclidean algorithm.
-- Given non-negative a and b, return x, y and g
-- such that ax + by = g, where g = gcd(a,b).
-- Note that x or y may be negative.
gcdExt :: Integer -> Integer -> (Integer, Integer, Integer)
gcdExt a 0 = (1, 0, a)
gcdExt a b =
let (q, r) = quotRem a b
(s, t, g) = gcdExt b r
in (t, s - q * t, g)AsymmetricEncryption/RabinMiller.hs
#!/usr/bin/runghc
module RabinMiller where
-- https://programmingpraxis.com/wp-content/uploads/2012/09/primenumbers.pdf
-- https://programmingpraxis.com/programming-with-prime-numbers-source-code-in-haskell/
import Control.Monad (forM_, when)
import Control.Monad.ST
import Data.Array.ST
import Data.Array.Unboxed
import Data.List (sort)
ancientSieve :: Int -> UArray Int Bool
ancientSieve n = runSTUArray $ do
bits <- newArray (2, n) True
forM_ [2 .. n] $ \p -> do
isPrime <- readArray bits p
when isPrime $ do
forM_ [2 * p, 3 * p .. n] $ \i -> do
writeArray bits i False
return bits
ancientPrimes :: Int -> [Int]
ancientPrimes n =
[ p
| (p, True) <-
assocs $ ancientSieve n
]
sieve :: Int -> UArray Int Bool
sieve n = runSTUArray $ do
let m = (n - 1) `div` 2
r = floor . sqrt $ fromIntegral n
bits <- newArray (0, m - 1) True
forM_ [0 .. r `div` 2 - 1] $ \i -> do
isPrime <- readArray bits i
when isPrime $ do
let a = 2 * i * i + 6 * i + 3
b = 2 * i * i + 8 * i + 6
forM_ [a, b .. (m - 1)] $ \j -> do
writeArray bits j False
return bits
primes :: Int -> [Int]
primes n = 2 : [2 * i + 3 | (i, True) <- assocs $ sieve n]
tdPrime :: Int -> Bool
tdPrime n = prime (2 : [3, 5 ..])
where
prime (d : ds)
| n < d * d = True
| n `mod` d == 0 = False
| otherwise = prime ds
tdFactors :: Int -> [Int]
tdFactors n = facts n (2 : [3, 5 ..])
where
facts n (f : fs)
| n < f * f = [n]
| n `mod` f == 0 =
f : facts (n `div` f) (f : fs)
| otherwise = facts n fs
powmod :: Integer -> Integer -> Integer -> Integer
powmod b e m =
let times p q = (p * q) `mod` m
pow b e x
| e == 0 = x
| even e =
pow
(times b b)
(e `div` 2)
x
| otherwise =
pow
(times b b)
(e `div` 2)
(times b x)
in pow b e 1
isSpsp :: Integer -> Integer -> Bool
isSpsp n a =
let getDandS d s =
if even d
then getDandS (d `div` 2) (s + 1)
else (d, s)
spsp (d, s) =
let t = powmod a d n
in if t == 1 then True else doSpsp t s
doSpsp t s
| s == 0 = False
| t == (n - 1) = True
| otherwise = doSpsp ((t * t) `mod` n) (s - 1)
in spsp $ getDandS (n - 1) 0
isPrime :: Integer -> Bool
isPrime n =
let ps =
[ 2,
3,
5,
7,
11,
13,
17,
19,
23,
29,
31,
37,
41,
43,
47,
53,
59,
61,
67,
71,
73,
79,
83,
89,
97
]
in n `elem` ps || all (isSpsp n) ps
rhoFactor :: Integer -> Integer -> Integer
rhoFactor n c =
let f x = (x * x + c) `mod` n
fact t h
| d == 1 = fact t' h'
| d == n = rhoFactor n (c + 1)
| isPrime d = d
| otherwise = rhoFactor d (c + 1)
where
t' = f t
h' = f (f h)
d = gcd (t' - h') n
in fact 2 2
rhoFactors :: Integer -> [Integer]
rhoFactors n =
let facts n
| n == 2 = [2]
| even n = 2 : facts (n `div` 2)
| isPrime n = [n]
| otherwise =
let f = rhoFactor n 1
in f : facts (n `div` f)
in sort $ facts n
-- main = do
-- print $ ancientPrimes 100
-- print $ primes 100
-- print $ length $ primes 1000000
-- print $ tdPrime 716151937
-- print $ tdFactors 8051
-- print $ powmod 437 13 1741
-- print $ isSpsp 2047 2
-- print $ isPrime 600851475143
-- print $ isPrime 2305843009213693951
-- print $ rhoFactors 600851475142AsymmetricEncryption/RSACipher.hs
#!/usr/bin/runghc
import CryptoMath
import Data.Char
import Data.Maybe (fromJust)
import RabinMiller
import System.Random
-- Note: The keysize here is 2^64, so you can see the numbers on the screen.
-- Normal key size is 2^4096...
genLargePrime :: IO Integer
genLargePrime = do
bigRand <- randomRIO (2 ^ 63, 2 ^ 64) :: IO Integer
if isPrime bigRand then return bigRand else genLargePrime
genPQ :: IO (Integer, Integer)
genPQ = do
p <- genLargePrime
q <- genLargePrime
if p /= q then return (p, q) else genPQ
genCoPrime :: Integer -> IO Integer
genCoPrime phiN = do
bigRand <- randomRIO (2 ^ 63, 2 ^ 64) :: IO Integer
if gcd' bigRand phiN == 1 then return bigRand else genCoPrime phiN
genKeys :: IO ((Integer, Integer), (Integer, Integer))
genKeys = do
(p, q) <- genPQ
let n = p * q
phiN = (p - 1) * (q - 1)
e <- genCoPrime phiN
let d = fromJust (modInv e phiN)
return ((n, e), (n, d))
encryptBlock :: (Integer, Integer) -> Integer -> Integer
encryptBlock (n, e) block = fastpow block e n
decryptBlock :: (Integer, Integer) -> Integer -> Integer
decryptBlock (n, d) block = fastpow block d n
main :: IO ()
main = do
let message = "This is a small message."
putStrLn ("Message was: " ++ message)
let codePoints = map (toInteger . ord) message
putStrLn ("\nCodePoints were: " ++ show codePoints)
(pubKey, privKey) <- genKeys
putStrLn ("\npubKey was: " ++ show pubKey)
putStrLn ("\nprivKey was: " ++ show privKey)
let encryptedPoints = map (encryptBlock pubKey) codePoints
putStrLn ("\nEncrypted message: " ++ show encryptedPoints)
let decryptedPoints = map (decryptBlock privKey) encryptedPoints
putStrLn ("\nDecrypted points: " ++ show decryptedPoints)
let decryptedText = map (chr . fromIntegral) decryptedPoints
putStrLn ("\nDecrypted text: " ++ decryptedText)To make textbook RSA actually secure,
padding on the encoded plaintext must be used:
https://en.wikipedia.org/wiki/Optimal_asymmetric_encryption_padding
If your RSA key is compromised,
what happens to past communications?
Should you keep using the key?
Forward secrecy protects the past…
This is something of a misnomer.
https://en.wikipedia.org/wiki/Diffie%E2%80%93Hellman_key_exchange
https://en.m.wikipedia.org/wiki/Multiplicative_group_of_integers_modulo_n
https://en.wikipedia.org/wiki/Discrete_logarithm_problem
https://en.m.wikipedia.org/wiki/Primitive_root_modulo_n
https://en.m.wikipedia.org/wiki/Generating_set_of_a_group
In modular arithmetic,
some number g, is a primitive root modulo n,
if every number, a, co-prime to n,
is congruent to a power of g modulo n.
That is, g is a primitive root modulo n,
if for every integer, a, co-prime to n,
there is an integer, k,
such that \(g^k \equiv a \mod n\).
For example, g = 3, mod 7:
Here we see that the period of 3k modulo 7 is 6.
The remainders in the period,
which are 3, 2, 6, 4, 5, 1,
form a rearrangement of all nonzero remainders modulo 7,
implying that g = 3 is indeed a primitive root modulo 7.
It was the first published public-key algorithm,
by Diffie and Hellman in 1976.
They first explained public key concepts.
It is used in a number of applications.
It is a practical method to exchange a secret key securely,
that can then be used for subsequent encryption of messages.
Security relies on difficulty of computing discrete logarithms.
Mention:
We previewed this “baby Diffie-Hellman idea before,
using nothing but exponents and log:
CryptoMath.html
Two people, Alice (A) annd Bob (B).
Example Public Parameters:
Prime number: q = 353
Primitive root of q: \(\alpha = 3\)
Example Private Parameters:
Alice randomly selects XA = 97
Bob randomly selects XB = 233
Alice and Bob each compute their public keys:
Alice computes YA = 397 mod 353 = 40
Bob computes YB = 3233 mod 353 = 248
Then exchange the public keys and compute secret key:
Alice:
\(K = (Y_B)^{X_A} \mod 353 = 248^{97} \mod 353
= 160\)
Bob:
\(K = (Y_A)^{X_B} \mod 353 = 40^{233} \mod 353
= 160\)
160 is the shared secret they both possess.
Diffie-Hellman Key Exchange, Generation and Computation
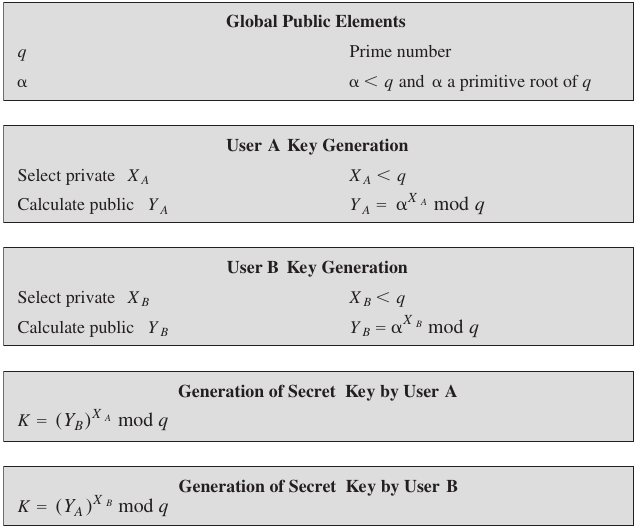
Diffie-Hellman Key Exchange
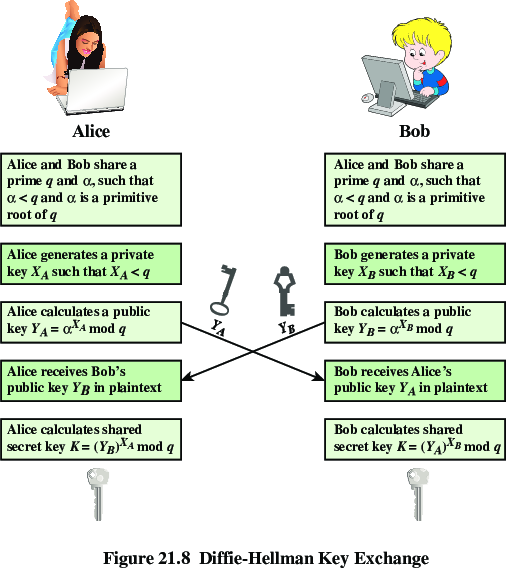
red = secret
blue = public
(against DH, RSA, or any other of these algorithms)
https://en.wikipedia.org/wiki/Man-in-the-middle_attack
Example of evil Eve in the middle:
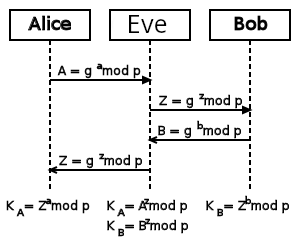
1. Alice transmits YA to Bob.
2. Eve generates private keys XD1 and XD2, and
their public keys YD1 and YD2
3. Eve intercepts YA and transmits YD1 to
Bob.
4. Eve also calculates \(K2 =
(Y_A)^{X_{D2}}\)
5. Bob receives YD1 and calculates \(K1 = (Y_{D1})^{X_B}\)
6. Bob transmits YB to Alice
7. Eve intercepts YB and transmits YD2 to
Alice
8. Eve calculates \(K1 =
(Y_B)^{X_{D1}}\)
9. Alice receives YD2 and calculates \(K2 = (Y_{D2})^{X_A}\)
If Alice and Bob were using these DH secrets as single-session
private keys,
which communications are compromised, past, present, or future?
+++++++++++++++++++++
Cahoot-08.4
When setting up your web server:
Use DH-* with TLS for this nice feature:
https://en.wikipedia.org/wiki/Transport_Layer_Security#Key_exchange_or_key_agreement
More to come later.
Using something like super-Turing solutions:
Which algorithms would primarily be directly vulnerable,
symmetric or asymmetric?
Even if both are not, does it matter?
If you are interested:
https://www.youtube.com/watch?v=lvTqbM5Dq4Q
https://aip.scitation.org/doi/abs/10.1063/1.4975761
https://arxiv.org/pdf/1512.05064.pdf