This MAC is not the same MAC term as:
a media access control (MAC) address,
or the mandatory access control (MAC) permissions control,
nor as the big MAC…
To err is human;
to make a real mess,
you need a computer.
document.querySelector('video').playbackRate = 1.2Chapter 10 - Hash functions
https://github.com/crypto101/crypto101.github.io/raw/master/Crypto101.pdf
(a quick aside on crypto-systems)
More to come later, here: AppliedCryptoSystems.html
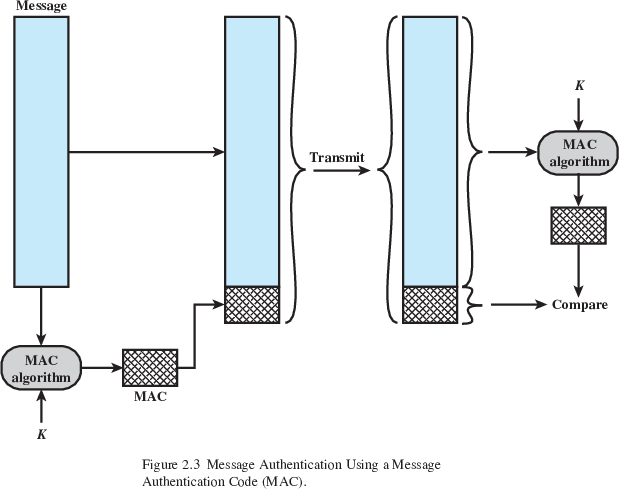
Authentication:
Protects against active attacks.
Verifies a received message is authentic and that:
message contents have not been altered,
a message is from an authentic source,
message delivery is in the correct sequence.
Can use conventional encryption as part of a larger system (or other methods).
Only sender and receiver share a key.
MAC is an over-overloaded term!
This MAC is not the same MAC term as:
a media access control (MAC) address,
or the mandatory access control (MAC) permissions control,
nor as the big MAC…

Alice (A) and Bob (B), share a common secret key KAB and compute a MAC.
MACM = F(KAB, M)
Where F():
DES is used to generate an encrypted version of the message,
and the last number of bits of ciphertext are used as the code.
A 16 or 32 bit code is typical.
Is this reversible or lossy?
+++++++++++++++++++++
Cahoot-11.1
Unlike a MAC, a hash function does not take secret key as
input.
Unlike symmetric or asymmetric cryptography,
it is not reversible (there is information loss).
This is like a deterministic meat grinder for your data:
The goal of authentication can be satisfied using hashing as part of
a system:
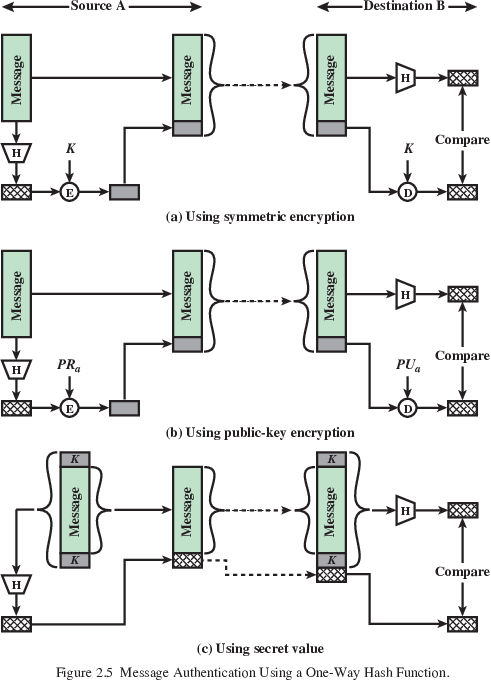
Enumerated descriptions below correspond to images above:
encrypt hash of message with pre-exchanged symmetric key
(must coordinate key exchange)
encrypt hash of message with public key
(no need to coordinate key exchange, assuming authentication
method)
hash function over the concatenation of the secret key and the
message:
Where || is simple concatenation,
H() is your hash function,
M is message,
and K is key,
MDM = H( K || M || K ).
Can be applied to a block of data of any size.
Produces a fixed-length output.
H(x) should be relatively easy to compute, for any given x.
Exception to this idea:
Key derivation functions and slow hash functions should ideally be
slow!
One-way or pre-image
resistant.
Assuming H(x) = h,
it should be computationally infeasible to find x.
Weak collision resistant
Given x,
it should be computationally infeasible to find y != x,
such that H(y) = H(x).
Strong collision resistance.
It should be computationally infeasible to find any pair (x, y),
such that H(x) = H(y).
+++++++++++++++++++++
Cahoot-11.2
There are two approaches to attacking a secure hash function:
Passwords:
Hash of a password is stored by an operating system (better when this is
a slow hash).
Intrusion detection:
Store H(F) for each file on a system and secure the hash values
There are a number of hash functions.
SHA family is most widely used hashing algorithms
SHA-3 is one:
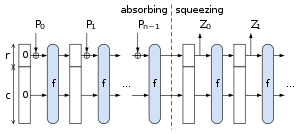
Uses A sponge construction.
Data is “absorbed” into the sponge,
then the result is “squeezed” out.
In absorbing phase,
message blocks are XOR’ed into a subset of the state,
which is then transformed as a whole using a permutation function
f.
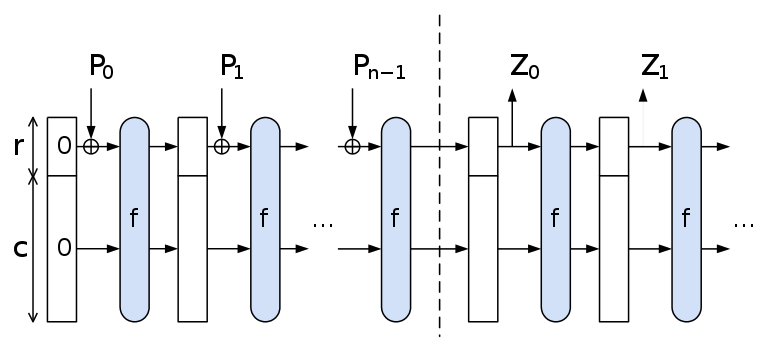
Pi are input, Zi are hashed output.
The unused “capacity” c should be twice the desired,
to insure resistance to collision or pre-image attacks.
More details later!
https://en.wikipedia.org/wiki/Cryptographic_hash_function
An ideal cryptographic hash function should have the
following properties, that:
1. it is deterministic, so the same message always results in the same
hash
it is relatively efficient to compute the hash value for any given message
it is not feasible to generate a message from its hash value, except by trying all possible messages
a small change to a message should change the hash value extensively, so that the new hash value appears uncorrelated with the old hash value.
it is not feasible to find two different messages with the same hash value
Functions of hashing include:
Verifying the integrity of messages and files.
Cryptographic signature generation and verification.
Password verification.
Proof-of-work (e.g., bitcoin).
File or data identifier.
Hashing is not typically sufficient for authentication alone!
Fold your message into a matrix (notice a pattern yet??), then XOR
down columns:
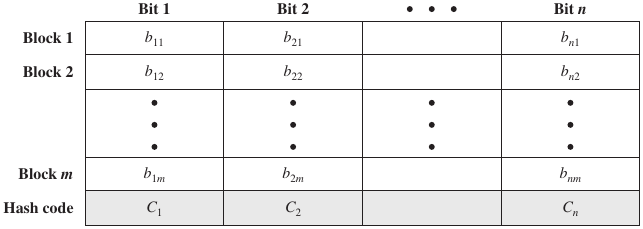
Ask:
Is this a robust and/or secure hash function?
Why?
Can we recover the message from the hash?
Is there data-loss here?
Why?
One-way
The most important property of a hash function is being
one-way:
Easy to compute, but hard to “invert”.
Inversion with hashing is not really even inversion at all, but
re-generation.
Given M, it should be somewhat easy to compute h(M).
Given y = h(M), it should be hard to find M.
Collision resistant
Cryptographic hash functions should be collision
resistant:
It should be hard to find two messages with the same hash value.
Given M, it should be hard to find a different message M’ such that
h(M’) = h(M).
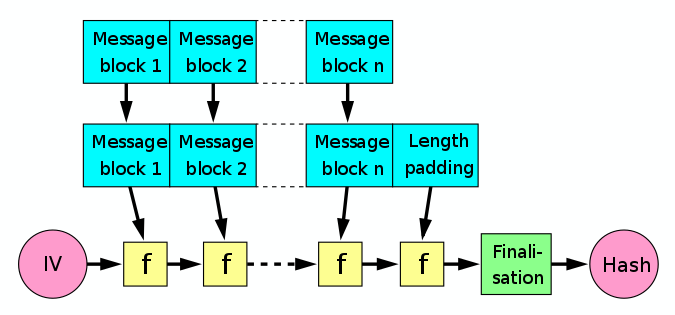
f is a one-way compression function.
Truly 1-way, not reversible, unlike encryption,
with hashing producing real formal information loss.
Used for MD5, SHA-1, and SHA-2 below:
https://en.wikipedia.org/wiki/MD5
MD5 is not considered secure, and is vulnerable to finding
collisions.
It should only be used for applications not requiring cryptographic
security.
Example when NOT to use md5:
expand on downloading an apk from outside an app store.
In python
#!/usr/bin/python3
import hashlib
hashlib.md5('stringtohash').hexdigest()
hashlib.md5('stringtohash_plusMitMinjection').hexdigest()
help(md5)In bash
#!/bin/bash
echo "hey" >filetohash.txt
md5sum filetohash.txt
echo "hey" >>filetohash.txt
md5sum filetohash.txthttps://en.wikipedia.org/wiki/Secure_Hash_Algorithms
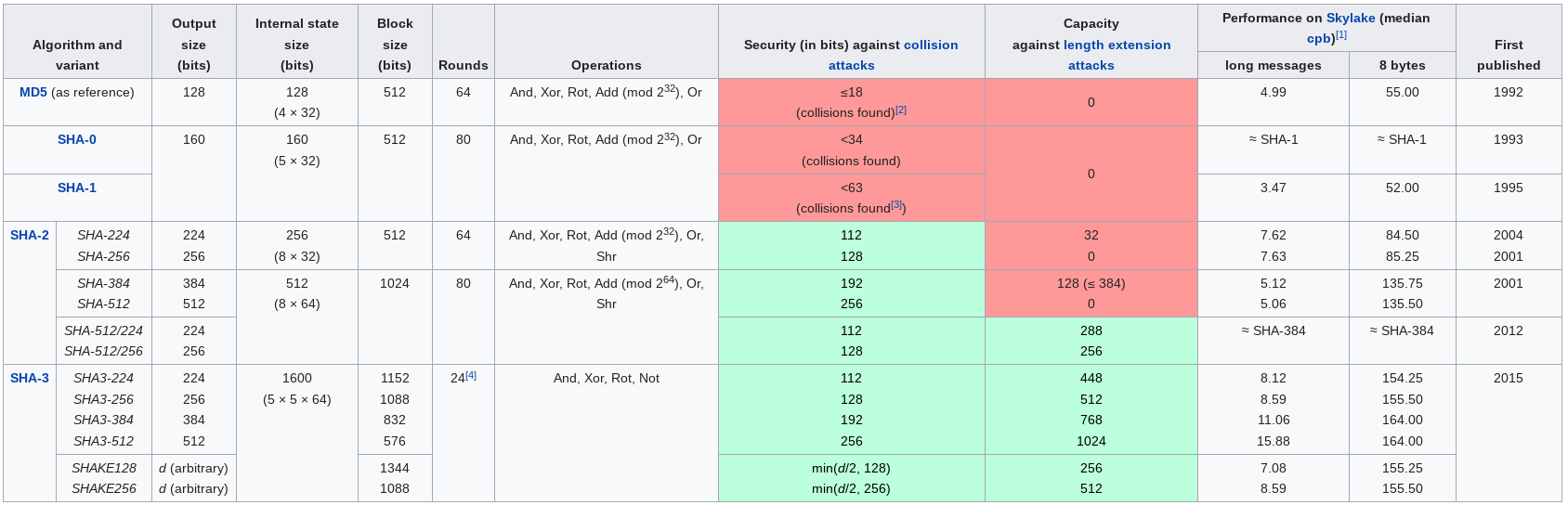
The Secure Hash Algorithms (SHA) are a family of
cryptographic hash functions published by the National Institute of
Standards and Technology (NIST) as a U.S. Federal Information Processing
Standard (FIPS), including:
SHA-0:
A retronym applied to the original version of the 160-bit hash
function,
published in 1993 under the name “SHA”.
It was withdrawn shortly after publication,
due to an undisclosed “significant flaw”,
and replaced by the slightly revised version SHA-1.
SHA-1:
A 160-bit hash function which resembles the earlier MD5 algorithm.
This was designed by the National Security Agency (NSA),
to be part of the Digital Signature Algorithm.
Cryptographic weaknesses were discovered in SHA-1,
and the standard was no longer approved for most cryptographic uses
after 2010.
SHA-2:
A family of two similar hash functions,
with different block sizes,
known as SHA-256 and SHA-512.
They differ in the word size;
SHA-256 uses 32-bit words where SHA-512 uses 64-bit words.
There are also truncated versions of each standard,
known as SHA-224, SHA-384, SHA-512/224 and SHA-512/256.
These were also designed by the NSA.
SHA-3:
A hash function formerly called Keccak,
chosen in 2012 after a public competition among non-NSA designers.
It supports the same hash lengths as SHA-2,
and its internal structure differs significantly from the rest of the
SHA family.
https://en.wikipedia.org/wiki/SHA-1
Takes arbitrary data as input,
outputs a 160-bit (20-byte) hash value,
known as a message digest,
typically rendered as a hexadecimal number, 40 digits long.
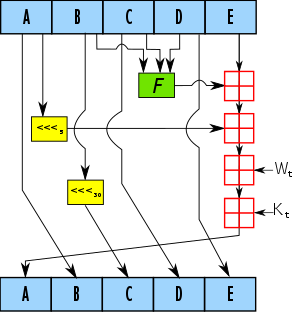
One iteration within the SHA-1 compression function:
A, B, C, D and E are 32-bit words of the state.
F is a nonlinear function that varies.
<<<n (Left shift n) denotes a left bit rotation by
n places,
where n varies for each operation.
Wt is the expanded message word of round t.
Kt is the round constant of round t.
Red square denotes addition modulo 232.
In python
From bash
#!/bin/bash
echo "hey" >filetohash.txt
sha1sum filetohash.txt
man sha1sum
# or
rhash --sha1 filetohash.txt
man rhashSHA was originally developed by NIST.
Published as FIPS 180 in 1993.
Was revised in 1995 as SHA-1 (Produces 160-bit hash values).
NIST issued revised FIPS 180-2 in 2002.
Adds 3 additional versions of SHA.
SHA-256, SHA-384, SHA-512,
256/384/512-bit hash values.
Same basic structure as SHA-1, but greater security.
In 2005 NIST announced the intention to phase out approval of
SHA-1,
and move to a reliance on the other SHA versions by 2010
SHA-1 is not secure on its own,
but can be in the context of another system like HMAC
in bits
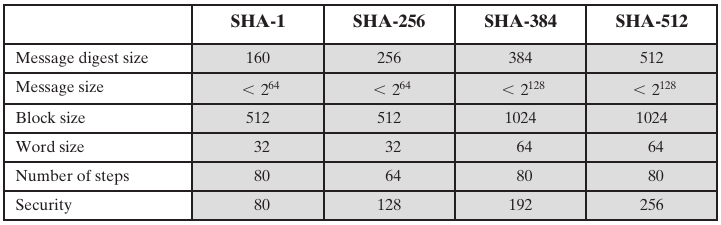
When you don’t see a -1 or -2 before the bit-size, it’s SHA-2.
For example, SHA-512 above is SHA-2-512 (below).
https://en.wikipedia.org/wiki/SHA-2
224-512 bit versions
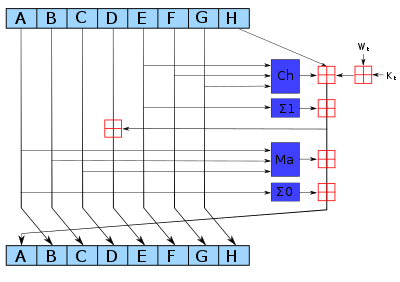
Similar to SHA-1, though an improvement.
Still vulnerable to extension attacks,
and thus needs to be used as part of a MAC,
if the goal is authentication.
In python
From bash
#!/bin/bash
# Note the sha binaries on my system:
ls /usr/bin/sha*
#/usr/bin/sha1hmac*
#/usr/bin/sha1sum*
#/usr/bin/sha224hmac*
#/usr/bin/sha224sum*
#/usr/bin/sha256hmac*
#/usr/bin/sha256sum*
#/usr/bin/sha384hmac*
#/usr/bin/sha384sum*
#/usr/bin/sha512hmac*
#/usr/bin/sha512sum*
echo "hey" >filetohash.txt
sha256sum filetohash.txt
sha512sum filetohash.txt
# or
rhash --sha256 filetohash.txt
rhash --sha512 filetohash.txtAs noted above, sha### is SHA-2, with the bit size specified.
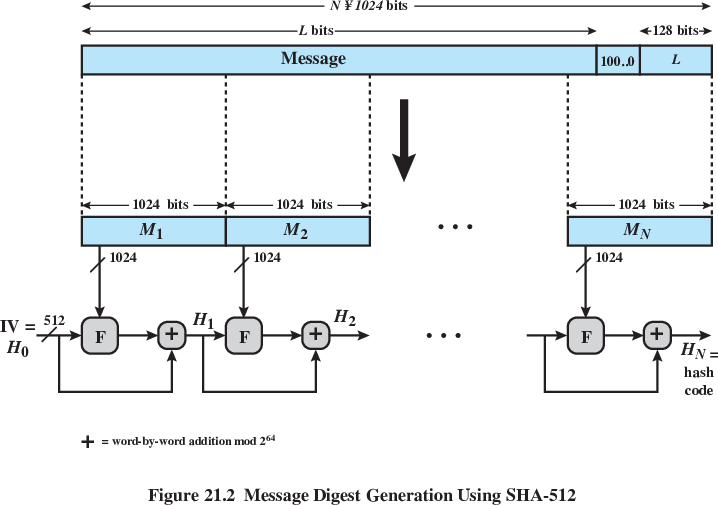
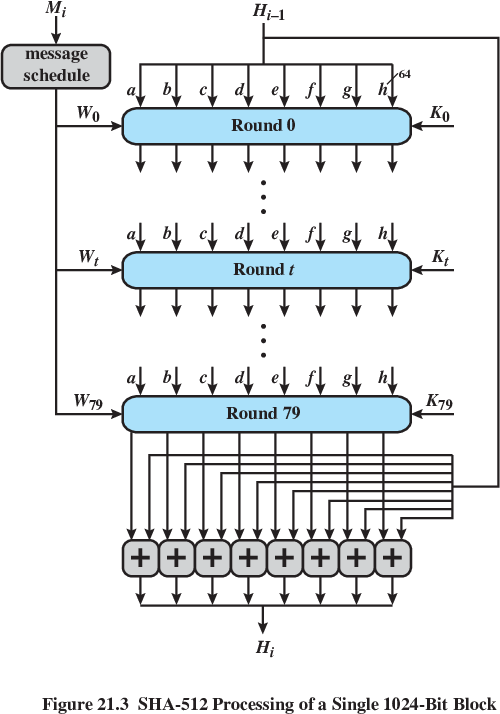
https://en.wikipedia.org/wiki/SHA-3
Is the first hash function we’re covering that is not
Merkle-Damgard,
and is a class of it’s own,
with some extra beneficial properties,
discussed below.
The sponge construction for hash functions:
Pi are input,
Zi are hashed output.
Data are “absorbed” into the sponge,
then the result is “squeezed” out.
In the absorbing phase,
message blocks are XOR’ed into a subset of the state,
which is then transformed as a whole using a permutation function
f.
In the “squeeze” phase,
output blocks are read from the same subset of the state,
alternated with the state transformation function f.
The size of the part of the state that is written and read is called the
“rate” (denoted r),
and the size of the part that is untouched by input/output is called the
“capacity” (denoted c).
In python
From bash
SHA-2 shared same structure and mathematical operations as its
predecessors,
and there was some concern for its future.
Due to time required to replace SHA-2,
should it become vulnerable,
NIST announced in 2007 a competition to produce SHA-3
SHA-3 does not need a MAC to be reasonably used for
authentication,
but HMAC is just an improvement anyway,
so you might as well use SHA-3 within HMAC, for example.
https://en.wikipedia.org/wiki/Key_derivation_function
A key derivation function (KDF) takes a secret initial value such
as:
a master key, a password, or a passphrase.
Using a pseudorandom function,
it derives one or more secret keys from that original value.
A KDF can be used to “stretch” keys into longer keys,
or to obtain keys of a required format,
such as converting a group element that is the result of a Diffie
Hellman key exchange,
into a symmetric key for use with AES.
They can ideally also be made slower to compute,
and thus are better for password hashing,
in key stretching and key
strengthening;
a fast hash enables brute forcing hashed passwords.
bcrypt and scrypt are popular KDFs.
We will talk about salt values in password hashing later…
(salt is another over-overloaded term).