
Meet Alice and Bob (and sometimes evil Eve)!
http://cryptocouple.com/ (show in class)
https://en.wikipedia.org/wiki/Alice_and_Bob

Meet Alice and Bob (and sometimes evil Eve)!
http://cryptocouple.com/ (show in class)
https://en.wikipedia.org/wiki/Alice_and_Bob
document.querySelector('video').playbackRate = 1.2http://inventwithpython.com/cracking/ Chapter 21
Our first modern encryption algorithm.
It’s also primitive.
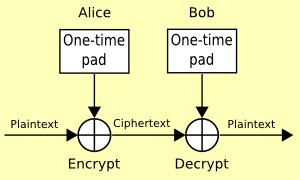
The only timeless encryption algorithm!
https://en.wikipedia.org/wiki/One-time_pad
http://users.telenet.be/d.rijmenants/en/onetimepad.htm

One Time Pad (OTP) is not the same thing as a One
Time Password (OTP):
https://en.wikipedia.org/wiki/One-time_password
is not what we’re talking about today.
What defines a “one time pad”?
The key is at least as long as the message or data that must be
encrypted.
The key is truly random.
It is not generated by a deterministic pseudo-random software
function.
Key and plain-text are calculated mod the encoding base,
for example:
modulo 10 (digits),
modulo 26 (letters), or
modulo 2 (binary)
mod also works as you would expect in binary (or any base).
Example mod 26:

Communication partners must securely pre-share their secret keys!
Information-theoretic security of the correctly implemented OTP is
truly perfect,
since the message contains absolutely no “information”.
Given a ciphertext from a correctly implemented OTP,
all plaintext messages are equally likely.
The following are equally likely:


+++++++++++++++++++++
Cahoot-06.1
Re-using a OTP key is the Vigenere cipher!


Cryptographically secure pseudo-random number
generator (CSPRNG)
or cryptographic pseudo-random number generator (CPRNG)
is a pseudo-random number generator (PRNG),
with properties that make it suitable for use in cryptography.
Pseudorandom number generators (PRNG)
also known as a deterministic random bit generator (DRBG),
is an algorithm for generating a sequence of numbers,
whose properties approximate the properties of sequences of random
numbers.
The PRNG-generated sequence is not truly random,
because it is completely determined by an initial value,
called the PRNG’s seed (which may include truly random values).
There are two primary methods used to generate random numbers.
Physical
The first method measures some physical phenomenon that
is expected to be random,
and then compensates for possible biases in the measurement
process.
Example sources include measuring atmospheric noise,
thermal noise, and other external electromagnetic or quantum
phenomena.
For example, cosmic background radiation or radioactive decay,
as measured over short timescales represent sources of natural
entropy.
In Linux distributions, the pseudo device file /dev/random
will block,
until sufficient entropy is harvested from the environment for
retrieval.
Computational
The second method uses deterministic computational
algorithms,
that can produce long sequences of apparently random results,
which are completely determined by a short initial seed value,
known as a seed value, key, or nonce.
As a result, the entire seemingly random sequence can be
reproduced,
if the seed value is known.
This type is often called a pseudorandom number
generator,
and typically does not continually rely on sources of naturally
occurring entropy,
though it may be periodically seeded by natural sources to compensate or
start.
+++++++++++++++++++++
Cahoot-06.2
The module random (random.random, etc.) and numpy.random are
not “truly” random:
https://docs.python.org/3/library/random.html
Use the module called secrets instead:
https://docs.python.org/3/library/secrets.html
The secrets module is used for generating cryptographically strong
random numbers.
It is suitable for managing data such as:
passwords, account authentication, security tokens, and related
secrets.
Secrets should be used in preference to the random module,
which is designed for modeling and simulation,
not for security or cryptography.
To generate a 55-long OTP key, for a 55-long message:
OneTimePad/secrets_demo.py
#!/usr/bin/python3
# -*- coding: utf-8 -*-
import secrets
otp: str = ""
for _ in range(55):
otp += secrets.choice("ABCDEFGHIJKLMNOPQRSTUVWXYZ .")
print(otp)
# or more concisely
otp = "".join([secrets.choice("ABCDEFGHIJKLMNOPQRSTUVWXYZ .") for _ in range(55)])
print(otp)or from /dev/random for a big integer:
OneTimePad/urandom_demo.py
#!/usr/bin/python3
# -*- coding: utf-8 -*-
import os
print(os.urandom(10))
# or
with open("/dev/random", "rb") as f:
print(int.from_bytes(f.read(10), "big"))You could post-process this into random characters.
See this for more detail on (/dev/urandom vs
/dev/random):
https://www.2uo.de/myths-about-urandom/
../../CompSciTools/Content/LinuxBash.html
Section # Generate random strings
#!/usr/bin/runghc
-- These methods are PRNG for statistics, not cryptography
module RandomExample where
import System.Random
main :: IO ()
main = do
-- Single item, ranged
singleIntRange <- randomRIO (1, 10) :: IO Int
print singleIntRange
singleFloatRange <- randomRIO (1, 10) :: IO Float
print singleFloatRange
singleCharRange <- randomRIO ('a', 'z') :: IO Char
print singleCharRange
-- Single item, default range bounds
singleIntDefault <- randomIO :: IO Int
print singleIntDefault
singleCharDefault <- randomIO :: IO Char
print singleCharDefault
-- Single item, ranged
rollDice <- getStdRandom (randomR ('a', 'z'))
print rollDice
rollDice2 <- getStdRandom (randomR (1, 10 :: Int))
print rollDice2
-- Single item, default range
rollDiceInt <- getStdRandom random :: IO Int
print rollDiceInt
rollDice2Char <- getStdRandom random :: IO Char
print rollDice2Char
-- You can choose the seed:
s1 <- getStdGen
let (i1, s2) = randomR (0, 100 :: Int) s1
-- The seed is passed, then chained:
let (i2, s3) = randomR (0, 100) s2 :: (Float, StdGen)
-- Default range
let (i3, s4) = random s3 :: (Int, StdGen)
putStrLn $ show i1 ++ ", " ++ show i2 ++ ", " ++ show i3
-- Using a seed, generate list of ranged ints, ranged
let randList = take 20 $ randomRs (0, 99 :: Int) s4
print randList
-- Generate list of ranged Chars, default range
putStrLn $ take 20 (randomRs ('a', 'z') s4)
-- You can choose the seed alternatively:
let rs = mkStdGen 42
let randFloats = take 20 $ randoms rs :: [Float]
print randFloats#!/usr/bin/runghc
-- This file implements this:
-- https://en.wikipedia.org/wiki/Fisher%E2%80%93Yates_shuffle
-- More background on Shuffle:
-- https://en.wikipedia.org/wiki/Random_permutation
-- https://en.wikipedia.org/wiki/Shuffling#Algorithms
-- https://wiki.haskell.org/Random_shuffle
-- https://www.reddit.com/r/haskell/comments/y8t3b/ask_rhaskell_how_to_elegantly_and_randomly/https://www.reddit.com/r/haskell/comments/y8t3b/ask_rhaskell_how_to_elegantly_and_randomly/
-- https://apfelmus.nfshost.com/articles/random-permutations.html
-- https://en.wikipedia.org/wiki/Steinhaus%E2%80%93Johnson%E2%80%93Trotter_algorithm
-- https://en.wikipedia.org/wiki/Heap%27s_algorithm
import Data.Map
import System.Random
shuffleStep :: (RandomGen g) => (Map Int a, g) -> (Int, a) -> (Map Int a, g)
shuffleStep (m, gen) (i, x) =
let (j, gen') = randomR (0, i) gen
in ((insert j x . insert i (m ! j)) m, gen')
shuffle :: (RandomGen g) => g -> [a] -> ([a], g)
shuffle gen [] = ([], gen)
shuffle gen l =
let toElems (x, y) = (elems x, y)
enumerate = zip [1 ..]
initial x gen = (singleton 0 x, gen)
in toElems $ Prelude.foldl shuffleStep (initial (head l) gen) (enumerate (tail l))
main :: IO ()
main = do
g <- getStdGen
print (shuffle g [1..10])#!/usr/bin/runghc
-- These methods do CSPRNG
-- https://stackoverflow.com/questions/20889729/how-to-properly-generate-a-random-bytestring-in-haskell
-- https://tommd.github.io/posts/RNG-Bench.html
-- ghc-crypto-api (old), ghc-cryptonite (retired), ghc-crypton (current) have similar API
-- sudo dnf install ghc-crypton-* ghc-entropy*
import Crypto.Random (getRandomBytes)
import Data.ByteString (ByteString)
import System.Entropy
generateSecureRandomBytes :: Int -> IO ByteString
generateSecureRandomBytes n = getRandomBytes n
main :: IO ()
main = do
-- With Crypton/Cryptonite/Crypto-api
randomBytes <- generateSecureRandomBytes 16
print randomBytes
-- With System.Entropy
randBytes <- getEntropy 16
print randBytesDiscussion Question:
Can you think of any practical issues with actually using the OTP?
Requires physical delivery for certainty of perfect
security.
Is this practical?
Do other algorithms have a similar constraint?
End-points are vulnerable.
As they are generally, in most security systems.
What else is like this?
Each key is used only once.
Is this practical?
How?
There should only be n copies of the key(s) for n parties,
one for each sender and one for each receiver.
The key material must be securely destroyed after use,
to ensure the key material is never reused,
and to protect the messages sent.
How?
Because the key material must be transported from one endpoint to
another,
and persists until the message is sent or received,
it can be more vulnerable to forensic recovery,
compared to the transient plaintext it protects.
How, when?
A simple hack/conversion of some code from our previous
algorithms:
OneTimePad/otp.py
#!/usr/bin/python3
# -*- coding: utf-8 -*-
"""
How could this code be improved?
@author: taylor@mst.edu
"""
import secrets
LETTERS = "ABCDEFGHIJKLMNOPQRSTUVWXYZ ."
def keygen(keylen: int) -> str:
return "".join([secrets.choice(LETTERS) for _ in range(keylen)])
def main() -> None:
myMessage = (
"The generation of random numbers is too important to be left to chance."
)
myMode = "encrypt" # Set to either 'encrypt' or 'decrypt'.
if myMode == "encrypt":
myKey = keygen(len(myMessage))
print("Your ONE-TIME use key is:\n", myKey, "\n")
translated = translateMessage(myKey, myMessage, "encrypt")
elif myMode == "decrypt":
myKey = input("What was the ONE-TIME use key you securily pre-shared?")
translated = translateMessage(myKey, myMessage, "decrypt")
print("Your " + myMode + "ed message was:", translated)
def translateMessage(key: str, message: str, mode: str) -> str:
translated = [] # Stores the encrypted/decrypted message string.
keyIndex = 0
key = key.upper()
for symbol in message: # Loop through each symbol in message.
num = LETTERS.find(symbol.upper())
if num != -1: # -1 means symbol.upper() was not found in LETTERS.
if mode == "encrypt":
num += LETTERS.find(key[keyIndex]) # Add if encrypting.
elif mode == "decrypt":
num -= LETTERS.find(key[keyIndex]) # Subtract if decrypting.
num %= len(LETTERS) # Handle any wraparound.
# Add the encrypted/decrypted symbol to the end of translated:
if symbol.isupper():
translated.append(LETTERS[num])
elif symbol.islower():
translated.append(LETTERS[num].lower())
keyIndex += 1 # Move to the next letter in the key.
else:
# Append the symbol without encrypting/decrypting.
translated.append(symbol)
return "".join(translated)
if __name__ == "__main__":
main()
Ask:
Taken from which cipher in the book?
Could this be simplified?
Discuss:
This is a base-26 (or symbol-set size base) otp.
One could compute the OTP in any base.
Does the number of symbols impact strength?
Would it be weaker if there were only two symbols?
+++++++++++++++++++++
Cahoot-06.3
General symbol is \(\oplus\).
Subset of the bitwise operators in Python:
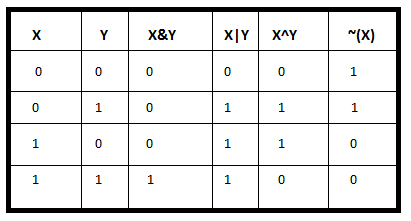
In interpreting the below code,
remember that the ints 1 and 0 are the same as the binary numbers 0 and
1.
The ^ operator operates on the binary representation of
int,
or directly on a binary string number,
e.g., 0b11111
OneTimePad/xor.py
#!/usr/bin/python3
# -*- coding: utf-8 -*-
import operator
print(1 ^ 0)
print(0 ^ 1)
print(1 ^ 1)
print(0 ^ 0)
# or where the operator lives
print(operator.xor(1, 0))
print(operator.xor(0, 1))
print(operator.xor(1, 1))
print(operator.xor(0, 0))
# Example on binary strings:
print(31 ^ 30)
print(bin(0b1111 ^ 0b1110))A clean, simple, and general OTP implementation:
P = {0, 1}n
C = {0, 1}n
P = {0, 1}n
E(p, k) = p \(\oplus\) k
D(c, k) = c \(\oplus\) k
Does it even matter what the key-space, plaintext, or ciphertext
space is?
What about in the lower limit of message length, 0 or 1 bit?
Encrypt by xor’ing input with key:

How to decrypt?
Just repeat to go backwards!
n = 5 the length of the data
p = 01011 which is 11
k = 10111 which is 23
c = p \(\oplus\) k
11100 = 01011 \(\oplus\) 10111
Also written as:
c = p ^ k
11100 = 01011 ^ 10111p = c \(\oplus\) k
01011 = 11100 \(\oplus\) 10111
Also written as:
p = c ^ k
01011 = 11100 ^ 10111#!/usr/bin/python3
# -*- coding: utf-8 -*-
n = 5
p = 0b01011
k = 0b10111
print("plaintext is:", p, bin(p))
print("key is:", k, bin(k))
c = p ^ k
print("ciphertext is:", c, bin(c))
p = c ^ k
print("recovered plaintext is:", p, bin(p))Original message is unambiguously recoverable with XOR,
but not other bit-wise operators, why?
https://www.devdungeon.com/content/working-binary-data-python
OneTimePad/numeric_bases_encoding.py (review in class)
These two are for you to ponder when doing this in python:
OneTimePad/ascii_newline.py
OneTimePad/ascii_nonewline.py
https://docs.python.org/3.7/howto/unicode.html
https://git-classes.mst.edu/taylorpat/python-otp
The permissions on this project are institutional.
You just have to be logged into git-classes to see it.
#!/usr/bin/python3
# -*- coding: utf-8 -*-
import sys
import secrets
def gen_keys(num_keys: int) -> list[str]:
"""
Takes the number of keys to generate as an integer input.
Generates num_keys keys.
Returns those keys in a list of str.
"""
keys: list[str] = []
for i in range(1, num_keys + 1):
keys.append(format(secrets.randbits(2048), "02048b"))
return keys
def main() -> None:
with open(sys.argv[1], "w") as code_book:
code_book.write("\n".join(gen_keys(50)))
if __name__ == "__main__":
main()#!/usr/bin/python3
# -*- coding: utf-8 -*-
import sys
def translate(text: str, key: str) -> str:
"""
Takes input of text as a string, and key as a string.
Translates the message.
Returns the translated message as a string.
"""
new_message = []
for i in range(256):
index = i * 8
newChar = chr(ord(text[i]) ^ int(key[index : index + 8], 2))
new_message.append(newChar)
return "".join(new_message)
def main() -> None:
key_num = int(sys.argv[2])
with open(sys.argv[1], "r") as code_book:
key = code_book.readlines()[key_num]
with open(sys.argv[3], "r", newline="") as input_text:
text = input_text.read()
with open(sys.argv[4], "w", newline="") as outputFile:
outputFile.write(translate(text, key))
if __name__ == "__main__":
main()#!/usr/bin/runghc
module OTP (translateString) where
import Data.Bits as B
import Data.Char as C
-- |
-- >>> translateChar 'k' 'Z'
-- '1'
-- |
-- >>> translateChar 'k' '1'
-- 'Z'
translateChar :: Char -> Char -> Char
translateChar keyChar messageChar = C.chr (B.xor (C.ord keyChar) (C.ord messageChar))
-- |
-- >>> translateString "HIYAVRX ZDVUW RFI AJ DYCPFGMAJKS" "\FS!02v?=S)%10wI!fz\DC2a)H%+0p*(#&de}"
-- "This message is 32 chars long..."
-- |
-- >>> translateString "HIYAVRX ZDVUW RFI AJ DYCPFGMAJKS" "This message is 32 chars long..."
-- "\FS!02v?=S)%10wI!fz\DC2a)H%+0p*(#&de}"
translateString :: String -> String -> String
translateString = zipWith translateChar
main :: IO ()
main = do
let message = "This message is 32 chars long..."
let key = "HIYAVRX ZDVUW RFI AJ DYCPFGMAJKS"
putStrLn "Your encrypted message is (with special characters interpreted):"
putStrLn (translateString key message)
putStrLn "Your encrypted message is (with special characters uninterpreted):"
print (translateString key message)
putStrLn "Your decrypted ciphertext is:"
putStrLn (translateString key (translateString key message))Several elegant lines of Haskell for the strongest known cryptography…
For personal text-based communications?
Has key-storage changed since this algorithm was used more widely?
For watching videos?
For video-chatting?
http://pidgin-paranoia.sourceforge.net/
There are many variants of the OTP, hardware, quantum, light,
etc.,
but they’re all just the OTP.
The next time you hear about some new exciting perfect
cryptography,
you’ll know it’s just the same old OTP!