1 06-PopularVariants

1.1 Popular Evolutionary Algorithm Variants

Now, we’ll describe some of the most widely known evolutionary algorithm variants.

Historical EA variants:

• Genetic Algorithms
• Evolution Strategies
• Evolutionary Programming
• Genetic Programming

More recent versions:

• Learning Classifier Systems
• Differential Evolution
• Particle Swarm Optimization
• Estimation of Distribution Algorithms
• Evolutionary Robotics
• Neuroevolution
• Many more!

1.2 Genetic Algorithms

https://en.wikipedia.org/wiki/Genetic_algorithm
http://scholarpedia.org/article/Genetic_algorithms
The genetic algorithm (GA) is the most widely known type of evolutionary algorithm.
GAs have largely (if mistakenly) been considered as function optimization methods.

1.2.1 Quick Overview

• Developed: USA in the 1960’s
• Early names: J. Holland, K. DeJong, D. Goldberg
• Holland’s original GA is now known as the simple genetic algorithm (SGA)
• Typically applied to:
  • discrete function optimization
  • binary representation
  • straightforward problems
  • now, used for benchmarks
• Features:
  • not too fast
  • SGA missing new variants (elitsm, sus)
  • often modeled by theorists
• Other GAs use different:
  • Representations
  • Mutations
  • Crossovers
  • Selection mechanisms

1.2.2 SGA technical summary

GAs employ:
a binary representation,
fitness proportionate selection,
a low probability of mutation,
an emphasis on genetically inspired recombination,
as a means of generating new candidate solutions.

1.2.3 SGA reproduction cycle

Select parents - for the mating pool.
(size of mating pool = population size)
Shuffle the mating pool.
Apply crossover - for each consecutive pair with probability p_c, otherwise copy parents.
Apply mutation - for each offspring (bit-flip with probability p_m independently for each bit).
Replace the whole population with the resulting offspring.

In detail:
GAs traditionally have a fixed work-flow:
given a population of μ individuals,
parent selection fills an intermediary population of μ,
allowing duplicates.
Then the intermediary population is shuffled to create random pairs,
and crossover is applied to each consecutive pair with probability p_c,
and the children replace the parents immediately.
The new intermediary population undergoes mutation individual by individual,
where each of the l bits in an individual is modified by mutation with independent probability p_m.
The resulting intermediary population forms the next generation replacing the previous one entirely.
Note that in this new generation there might be pieces,
perhaps complete individuals,
from the previous one that survived crossover and mutation without being modified,
but the likelihood of this is rather low (depending on the parameters μ, p_c, p_m).

1.2.4 An example after Goldberg ’89

• Simple problem: maximize x² over {0, 1, …, 31}
• GA approach:
  • Representation: binary code, e.g., 01101 ↔︎ 13
  • Population size: 4
  • 1-point x-over, bit-wise mutation
  • Roulette wheel selection
  • Random initialization
• We previously showed one generational cycle done by hand

1.2.5 X2 example

We covered this previously.

1.2.5.1 Selection

1.2.5.2 Crossover

1.2.5.3 Mutation

1.2.6 The simple GA

Has been subject of many (early) studies.
In the early years of the field,
there was significant attention paid to trying to establish suitable values for GA parameters,
such as the population size, crossover and mutation probabilities.
Recommendations were for mutation rates between 1/l and 1/μ,
crossover probabilities around 0.6-0.8,
and population sizes in the fifties or low hundreds,
although to some extent these values reflect the computing power available in the 1980s and 1990s.

1.2.6.1 Weaknesses

It has been recognized that there are some flaws in the SGA.
Shows many shortcomings, e.g.,
Representation is too restrictive.
Mutation and crossover operators are only applicable for bit-string and integer representations.
Selection mechanism is sensitive to converging populations with close fitness values.
Generational population model can be improved with explicit survivor selection.

1.2.6.2 New features

Various features have been added since the first SGA.
Factors such as elitism, and non-generational models were added to offer faster convergence if needed.
SUS is preferred to roulette wheel implementation,
and most commonly rank-based selection is used,
implemented via tournament selection for simplicity and speed.
Studying the biases in the interplay between representation and one-point crossover led to the development of alternatives,
such as uniform crossover,
and a stream of work through ‘messy-GAs’ and ‘Linkage Learning’,
to Estimation of Distribution Algorithms.
Analysis and experience has recognised the need to use non-binary representations where more appropriate.
The problem of how to choose a suitable fixed mutation rate has largely been solved by adopting the idea of self-adaptation,
where the rates are encoded as extra genes in an individuals representation and allowed to evolve.

1.3 Evolution Strategies

https://en.wikipedia.org/wiki/Evolution_strategy
http://scholarpedia.org/article/Evolutionary_strategies
This one was actually intended as a numerical optimization technique.

1.3.1 Quick overview

• Developed: Germany in the 1960’s
• Early names: I. Rechenberg, H.-P. Schwefel
• Typically applied to:
  • numerical optimization
• Attributed features:
  • fast
  • good optimizer for real-valued optimization
  • relatively much theory
• Special:
  • self-adaptation of (mutation) parameters standard

1.3.2 ES technical summary table

• μ is population number
• λ is offspring number

1.3.3 (1+1) ES

• Task: minimize f: \({\rm I\!R}^n\) in R

• Algorithm: “two-membered ES” using

  • Vectors from \({\rm I\!R}^n\) directly as chromosomes
  • Population size 1
  • Only mutation creating one child
  • Greedy selection

1.3.4 Adaptive mutation mechanism

• z values drawn from normal distribution N(ξ,σ)
  • mean ξ is set to 0
  • variation σ is called mutation step size
• σ is varied on the fly by the “1/5 success rule”:
  Rechenberg’s 1/5 success rule states that:
  the ratio of successful mutations to all mutations should be 1/5.
  Hence if the ratio is greater than 1/5,
  then the step size should be increased,
  and if the ratio is less than 1/5,
  then it should be decreased.
  The rule is executed at periodic intervals,
  for instance, after k iterations,
  each σ is reset by:
  σ = σ / c if p_s > 1/5
  σ = σ * c if p_s < 1/5
  σ = σ if p_s = 1/5
  where:
  p_s is the % of successful mutations
  constant c is \(0.8 \leq c \leq 1\)
  Using this mechanism,
  changes in the parameter values are now based on feedback from the search.

1.3.5 Illustration of normal distribution

1.3.6 Historical example: the jet nozzle experiment

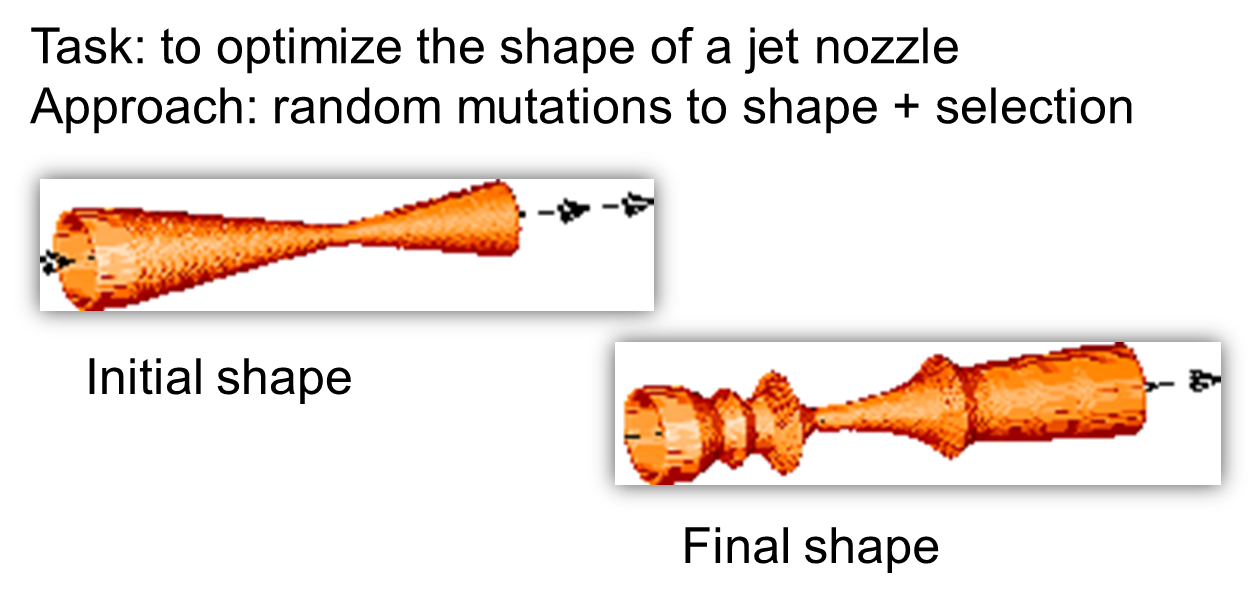
The original nozzle:


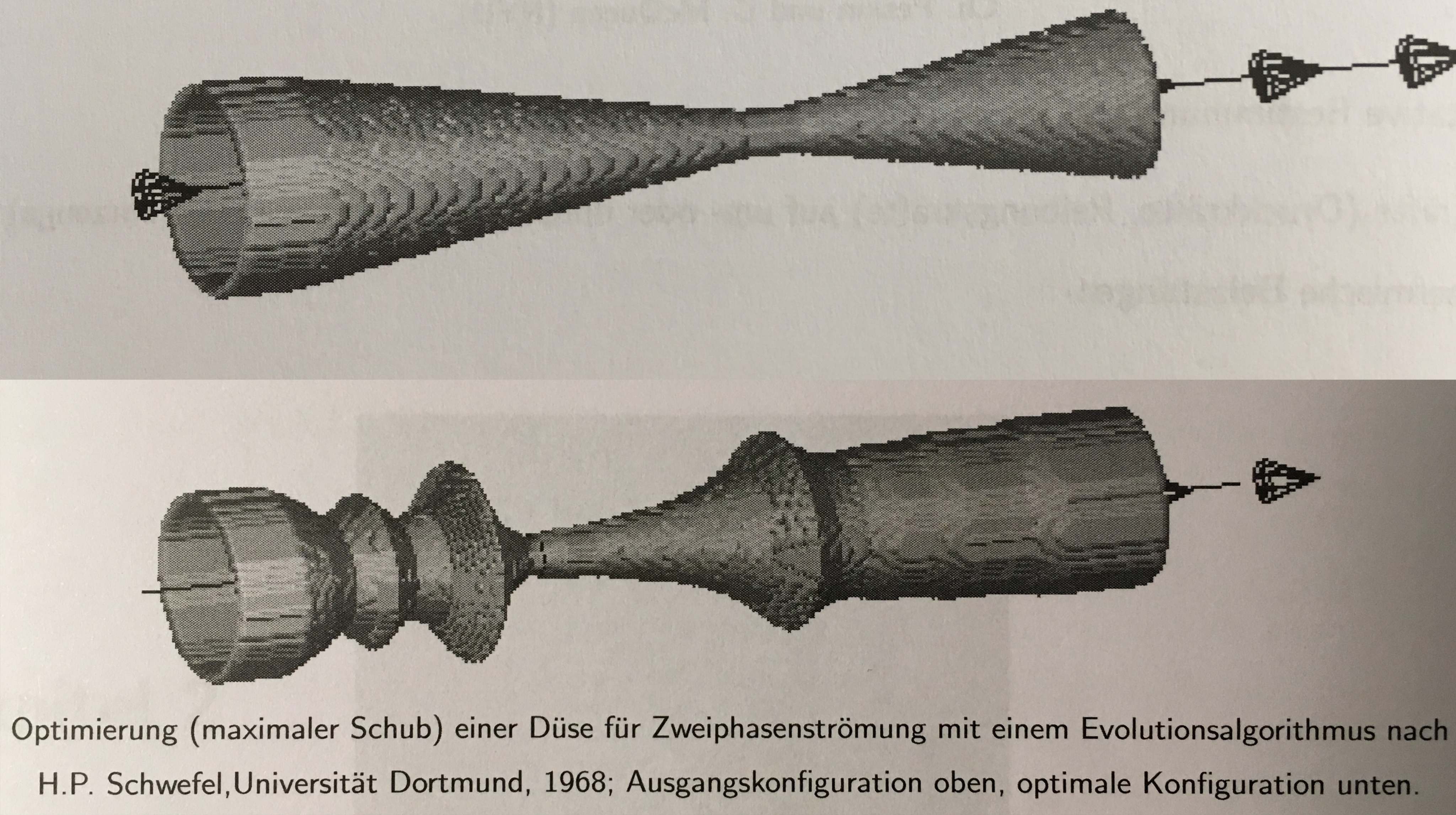
To actually build it:

Side note:
Lathing is one of the precursors of precision technologies:
https://www.youtube.com/watch?v=gNRnrn5DE58

1.3.7 Representation

ES works with extended chromosomes \(\bar{x}\), \(\bar{p}\),
where \(\bar{x} \in {\rm I\!R}^n\) is a vector from the domain of the given objective function to be optimized,
while \(\bar{p}\) carries the algorithm parameters.

• Chromosomes consist of three parts:
  • Object variables: x₁, …, x_n
  • Strategy parameters:
    • Mutation step sizes: \(\sigma_1, ..., \sigma_{n_\sigma}\)
    • Rotation angles: \(\alpha_1, ..., \alpha_{n_\alpha}\)
• Not every component is always present
• Full size: <x₁, …, x_n, σ₁,…,σ_n, α₁, …, α_k>
• where k = n(n-1)/2 (no. of i,j pairs)

1.3.8 Recombination

• Creates one child
• Acts per variable / position by either
  • Averaging parental values, or
  • Selecting one of the parental values
• From two or more parents by either:
  • Using two selected parents to make a child
  • Selecting two parents for each position

1.3.9 Names of recombinations

1.3.10 Parent selection

Parents are selected by uniform random distribution whenever an operator needs one/some.
Thus, ES parent selection is unbiased.
Every individual has the same probability to be selected.

1.3.11 Self-adaptation illustrated

• Given a dynamically changing fitness landscape (optimum location shifted every 200 generations)
• Self-adaptive ES is able to
  • follow the optimum and
  • adjust the mutation step size after every shift !
    

1.3.12 Prerequisites for self-adaptation

μ > 1 to carry different strategies.
λ > μ to generate offspring surplus.
(μ,λ)-selection to get rid of mis-adapted σ’s.
Mixing strategy parameters by (intermediary) recombination on them.

1.3.13 Selection Pressure

Is quite high for ES.
Takeover time \(\tau^*\) is a measure to quantify the selection pressure.
The number of generations it takes until the application of selection completely fills the population,
with copies of the best individual.
Goldberg and Deb showed:
For proportional selection in a genetic algorithm the takeover time is \(\lambda ln(\lambda)\)

1.3.14 Example application: The cherry brandy experiment

Task: to create a color mix yielding a target color (that of a well known cherry brandy).
Ingredients: water + red, yellow, blue dye
Representation: <w, r, y, b> no self-adaptation!
Values scaled to give a predefined total volume (30 ml).
Mutation: lo / med / hi values of σ used with equal chance.
Selection: (1,8) strategy
Fitness: students effectively making the mix and comparing it with target color
Termination criterion: student satisfied with mixed color
Solution is found mostly within 20 generations
Accuracy is very good.

1.3.15 Example application: The Ackley function (Bäck et al ’93)

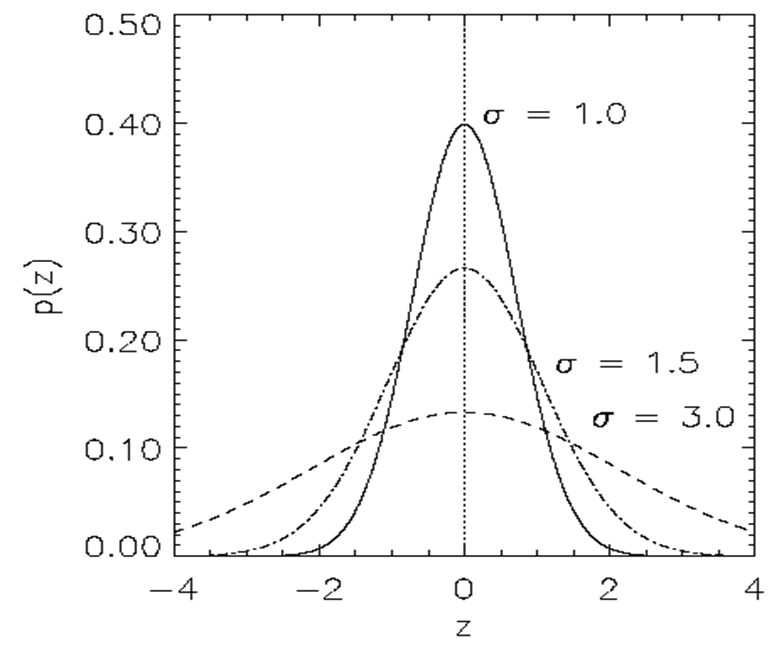
https://en.wikipedia.org/wiki/Ackley_function
The Ackley function is widely used for testing optimization algorithms,
much like an image dataset, or openAI gym, now.

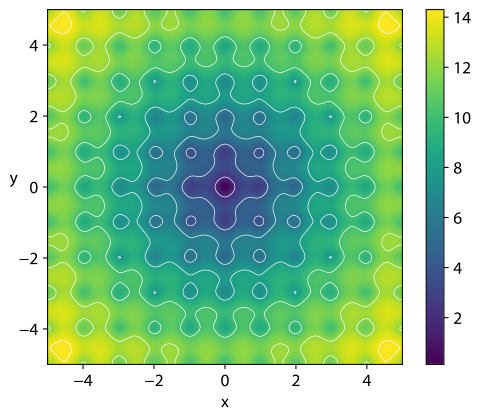
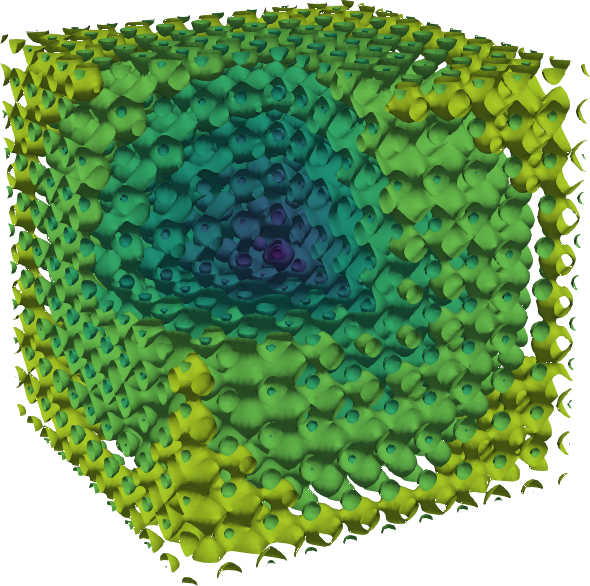
In its two-dimensional form, as shown in the plot above,
it is characterized by a nearly flat outer region,
and a large hole at the centre.
The function poses a risk for optimization algorithms,
particularly hillclimbing algorithms,
to be trapped in one of its many local minima.

• The Ackley function (here used with n=30):
  \(f(x,y)=-20\exp \left[-0.2{\sqrt{1/n)} \sum_{i=1}^n x^2_i}\,\right] -\exp \left[ 1/n \sum_{i=1}^n cos(2\pi x_i) \right]+e+20\)
• Evolution strategy:
  • Representation:
    • -30 < x_i < 30
    • 30 step sizes
  • (30,200) selection
  • Termination : after 200000 fitness evaluations
  • Results: average best solution is 7.48 x 10^-8 (very good)

1.4 Evolutionary Programming:

https://en.wikipedia.org/wiki/Evolutionary_programming
http://scholarpedia.org/article/Evolutionary_programming

1.4.1 Quick overview

• Developed: USA in the 1960’s
• Early names: D. Fogel
• Typically applied to:
  • traditional EP: prediction by finite state machines
  • contemporary EP: (numerical) optimization and beyond
• Attributed features:
  • now, very open framework: any representation and mutation operators OK
  • crossbred with ES (contemporary EP)
  • consequently: now, hard to say what “standard” EP is
• Special:
  • no recombination
  • self-adaptation of parameters standard (contemporary EP)

1.4.2 Technical summary table

1.4.3 Historical EP perspective

EP aimed at achieving intelligence
Intelligence was viewed as adaptive behavior
Prediction of the environment was considered a prerequisite to adaptive behavior
Thus: capability to predict is key to intelligence

1.4.4 Prediction by finite state machines

https://en.wikipedia.org/wiki/Finite-state_machine

The original paper:
Fogel, L.J., Owens, A.J., Walsh, M.J.
Artificial Intelligence Through Simulated Evolution
New York: John Wiley, 1966
A discussion of it:
06-PopularVariants/fogel66.pdf
06-PopularVariants/fogel66a.pdf
06-PopularVariants/fogel95.pdf

• Finite state machine (FSM):
  • States S
  • Inputs I
  • Outputs O
  • Transition function δ: S x I -> S x O
  • Transforms input stream into output stream
• Can be used for predictions,
• e.g. to predict next input symbol in a sequence

A population of FSMs is exposed to the environment, that is,
the sequence of symbols that has been observed up to the current time.
For each parent machine,
as each input symbol is presented to the machine,
the corresponding output symbol is compared with the next input symbol.
The worth of this prediction is then measured with respect to the payoff function
(e.g., all-none, squared error).
After the last prediction is made,
a function of the payoff for the sequence of symbols indicates the fitness of the machine or program
(e.g., average payoff per symbol).
Offspring machines are created by randomly mutating the parents,
and are scored in a similar manner.
Those machines that provide the greatest payoff are retained,
to become parents of the next generation,
and the process iterates.
When new symbols are to be predicted,
the best available machine serves as the basis for making such a prediction,
and the new observation is added to the available database.

1.4.5 General FSM example

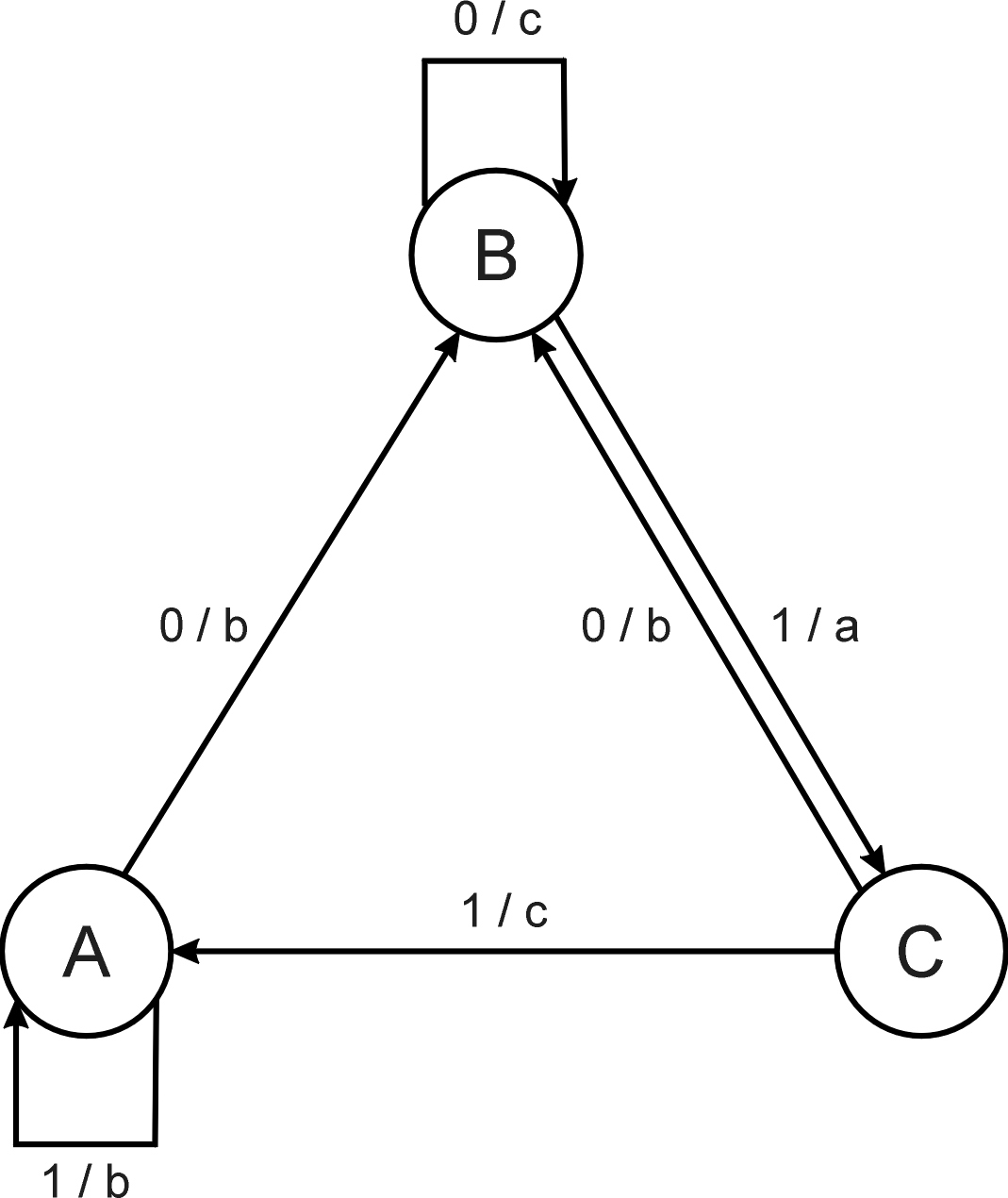
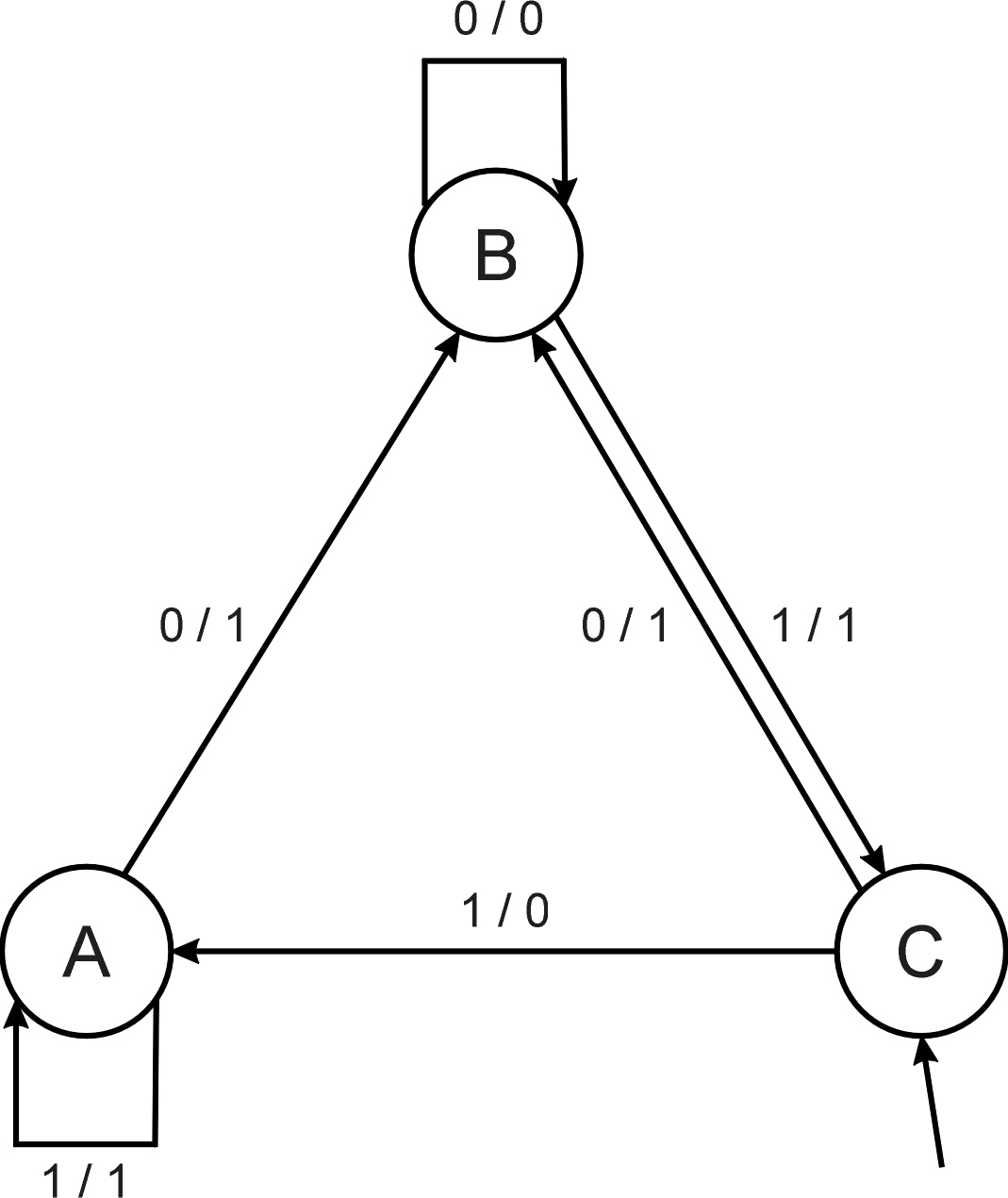
Consider the FSM with:
S = {A, B, C}
I = {0, 1}
O = {a, b, c}
δ given by a diagram (above).

1.4.6 FSM as predictor

Consider the following FSM
Task: predict next input
Quality (prediction accuracy): % of in_(i+1) = out_i
Given initial state C
Input sequence 011101
Leads to output 110111
Quality: 3 out of 5

1.4.7 Evolving FSMs to predict primes

• Evolve a function P, where:
  P(n) = 1 if n is prime, 0 otherwise
• I = N = {1, 2, 3, …, n, …}
• O = {0,1}
• Correct prediction: out_i= P(in(i+1))
• Fitness function:
  • 1 point for correct prediction of next input
  • 0 point for incorrect prediction
  • Penalty for “too many” states
• Parent selection: each FSM is mutated once
• Mutation operators (one selected randomly):
  • Change an output symbol
  • Change a state transition (i.e. redirect edge)
  • Add a state
  • Delete a state
  • Change the initial state
• Survivor selection: (μ+μ)
• Results: overfitting, after 202 inputs, the best FSM had one state, and both outputs were 0,
  • i.e., it always predicted “not prime”…
• Main point: not perfect accuracy, but demonstration that simulated evolutionary process can create good solutions for intelligent task.
• Not all approaches using FSM’s failed.
• Others were successful; this is just a funny one!

1.4.8 Modern EP

No predefined representation in general.
Thus, no predefined mutation (must match representation).
Often applies self-adaptation of mutation parameters.

1.4.9 Representation

• For continuous parameter optimization
• Chromosomes consist of two parts:
  • Object variables: x₁, …, x_n
  • Mutation step sizes: σ₁, …, σ_n
• Full size: <x₁, …, x_n, σ₁, …, σ_n>

1.4.10 Mutation

• Chromosomes: <x₁, …, x_n, σ₁, …, σ_n>
• σ_i’ = σ_i * (1 + α * N(0,1))
• x_i’ = x_i + σ_i’ * N_i(0,1)
• α ≈ 0.2
• boundary rule: σ’ < ε₀ ⇒ σ’ = ε₀
• Other variants proposed and tried:
  • Using variance instead of standard deviation
  • Mutate σ-last
  • Other distributions, e.g, Cauchy instead of Gaussian

Since the 1990s,
EP variants for optimization of real-valued parameter vectors have become more frequent,
and even positioned as “standard’ EP.
During the history of EP a number of mutation schemes,
such as one in which the step size is inversely related to the fitness of the solutions,
have been proposed.
Since the proposal of meta-EP,
self-adaptation of step sizes has become the norm.
Other ideas from ES have also informed the development of EP algorithms,
and a version with self-adaptation of covariance matrices, called R-meta-EP is also in use.
Worthy of note is Yao’s improved fast evolutionary programming algorithm (IFEP).
whereby two offspring are created from each parent,
one using a Gaussian distribution to generate the random mutations,
and the other using the Cauchy distribution.
The latter has a fatter tail
(i.e., more chance of generating a large mutation),
which the authors suggest gives the overall algorithm greater chance of escaping from local minima,
whilst the Gaussian distribution (if small step sizes evolve),
gives greater ability to fine-tune the current parents.

1.4.11 Recombination

Little to none, though it was present:
http://scholarpedia.org/article/Evolutionary_programming
Rationale:
One point in the search space stands for a species,
not for an individual and there can be no crossover between species.
Much historical debate “mutation vs. crossover”.
The issue of using a mutation-only algorithm versus a recombination and mutation variant has been intensively discussed since the 1990s.
“the traditional practice of setting operator probabilities at constant ,
… is quite limiting and may even prevent the successful discovery of suitable solutions.”

1.4.12 Parent selection

• Each individual creates one child by mutation
• Thus:
  • Deterministic
  • Not biased by fitness

1.4.13 Survivor selection

• Use survivor selection primarily

1.4.14 Evolving checkers players

06-PopularVariants/fogel02.pdf
Skim paper, figure of ANN at end.

• Neural nets for evaluating future values of moves are evolved
• NNs have fixed structure with 5046 weights, these are evolved + one weight for “kings”
• Representation:
  • vector of 5046 real numbers for object variables (weights)
  • vector of 5046 real numbers for σ’s
• Mutation:
  • Gaussian, lognormal scheme with σ-first
  • Plus special mechanism for the kings’ weight
• Population size 15

Tournament size q = 5
Programs (with NN inside) play against other programs,
no human trainer or hard-wired intelligence.
After 840 generation (6 months!),
best strategy was tested against humans via Internet.
Program earned “expert class” ranking,
outperforming 99.61% of all rated players.

NeuroEvolution
The checkers player is a kind of:
https://en.wikipedia.org/wiki/Neuroevolution
http://www.scholarpedia.org/article/Neuroevolution

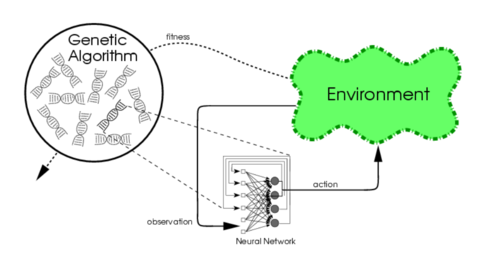
Evolutionary algorithms generate artificial neural networks (ANN),
their parameters, and their rules.
It is commonly used as part of the reinforcement learning paradigm,
and it can be contrasted with conventional deep learning techniques,
that use gradient descent on a neural network with a fixed topology.

Discussion question:
What happened to the field of EP’s evolving FSMs?

1.5 Genetic Programming

https://en.wikipedia.org/wiki/Genetic_programming
https://geneticprogramming.com/
https://www.genetic-programming.com/

1.5.1 History

The first record of the proposal to evolve programs is probably that of Alan Turing in the 1950s.
06-PopularVariants/turing50.pdf

Non-GP EC grew in the 60s and 70s,
but despite this progress,
there was a gap of some thirty years,
before Richard Forsyth demonstrated the successful evolution of small programs,
represented as trees,
to perform classification of crime scene evidence for the UK Home Office!
06-PopularVariants/beagle81.pdf

Although the idea of evolving programs,
initially in the computer language LISP,
was discussed among John Holland’s students,
it was not until they organized the first Genetic Algorithms conference in Pittsburgh,
that Nichael Cramer published evolved programs in two specially designed languages.
https://dl.acm.org/doi/10.5555/645511.657085

In 1988, another PhD student of John Holland,
John Koza, patented his invention of a GA for program evolution:
“Non-Linear Genetic Algorithms for Solving Problems”,
“United States Patent 4935877”, 1990

This was followed by publication in the International Joint Conference on Artificial Intelligence IJCAI-89.
06-PopularVariants/koza_ijcai1989.pdf

Then, Koza followed this with 205 publications on “Genetic Programming” (GP).
GP was a name coined by David Goldberg, also a PhD student of John Holland.
There was an enormous expansion of the number of publications.
In 2010, Koza listed 77 results where Genetic Programming was human competitive.
06-PopularVariants/koza_GPEM2010article.pdf

1.5.2 Quick overview

• Developed: Grew mostly in the USA in the 1990’s
• Early popularizer: J. Koza
• Typically applied to:
  • Machine learning tasks (prediction, classification…)
• Attributed features:
  • Competes with neural nets and alike
  • Often needs huge populations (thousands)
  • Slow
• Special:
  • non-linear chromosomes: trees, graphs
  • Mutation possible but not necessary

1.5.3 Theory

Genetic programming is a relatively young member of the evolutionary algorithm family.
EAs discussed so far are typically applied to optimization problems.
Most other EAs find some input, realizing maximum payoff.

GP could instead be positioned in machine learning.
GP is used to seek models with maximum fit.
Once maximization is introduced,
modeling problems can be seen as special cases of optimization.
This is the basis of using evolution for such tasks:
models, represented as parse trees,
are treated as individuals,
and their fitness is the model quality to be maximized.

Discussion question:
Might GP subsume other fields?
Does GP suffice in all cases where evolving an FSM might?
Would you guess GP has any disadvantages compared to simpler representations?

1.5.4 Basics

The parse trees used by GP as chromosomes are expressions in a given formal syntax.
Depending on the problem at hand,
and the users’ perceptions on what the solutions must look like,
this can be the syntax of arithmetic expressions,
formulas in first-order predicate logic,
or code written in a programming language.
In particular, they can be envisioned as executable source code,
that is, programs.
The syntax of functional programming,
e.g., the language LISP,
very closely matches the so-called Polish notation of expressions.
For instance, the formula we covered before:
\(2 \cdot \pi + ((x + 3) - \frac{y}{5+1})\)

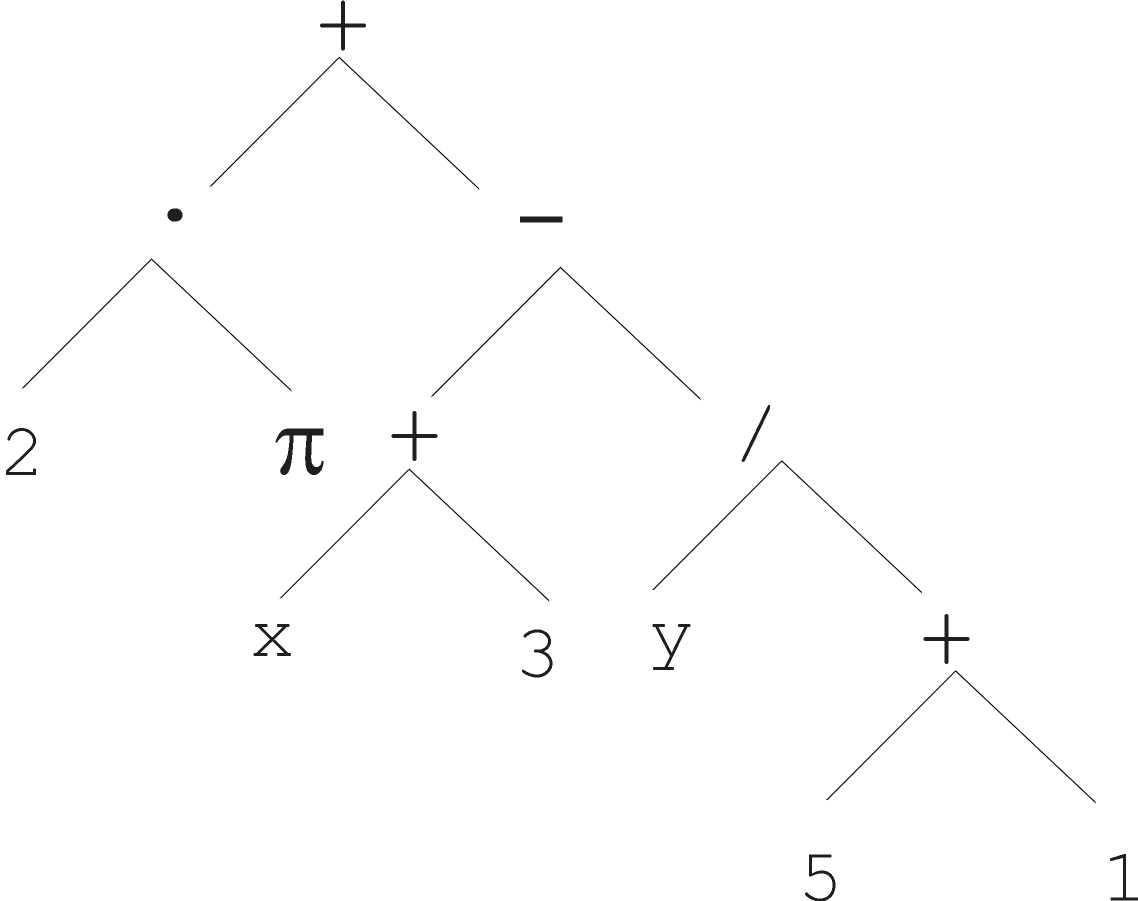
can be rewritten in this Polish notation as:
+(·(2, π), −(+(x, 3), /(y, +(5, 1)))),
while the executable LISP code1 looks like:
(+ (· 2 π) (− (+ x 3) (/ y (+ 5 1)))).
This is cool!

1.5.5 Technical summary table

Most are basic trees:

But, there are other flavors too (more below).

1.5.6 Example credit scoring

Bank wants to distinguish good from bad loan applicants
Model needed that matches historical data

A possible model:

IF (NoC = 2) AND (S > 80000) 
THEN good 
ELSE bad

In general:

IF formula 
THEN good 
ELSE bad

Only unknown is the right formula, hence:
Our search space (phenotypes) is the set of formulas.

Natural fitness of a formula:
percentage of well classified cases of the model it stands for.

IF (NoC = 2) AND (S > 80000)
THEN good  
ELSE bad

can be represented by the following tree

1.5.7 Offspring creation scheme

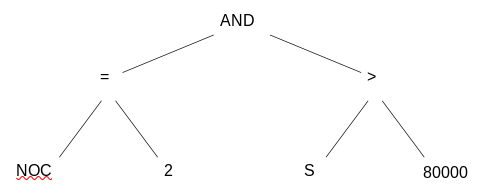
Compare:
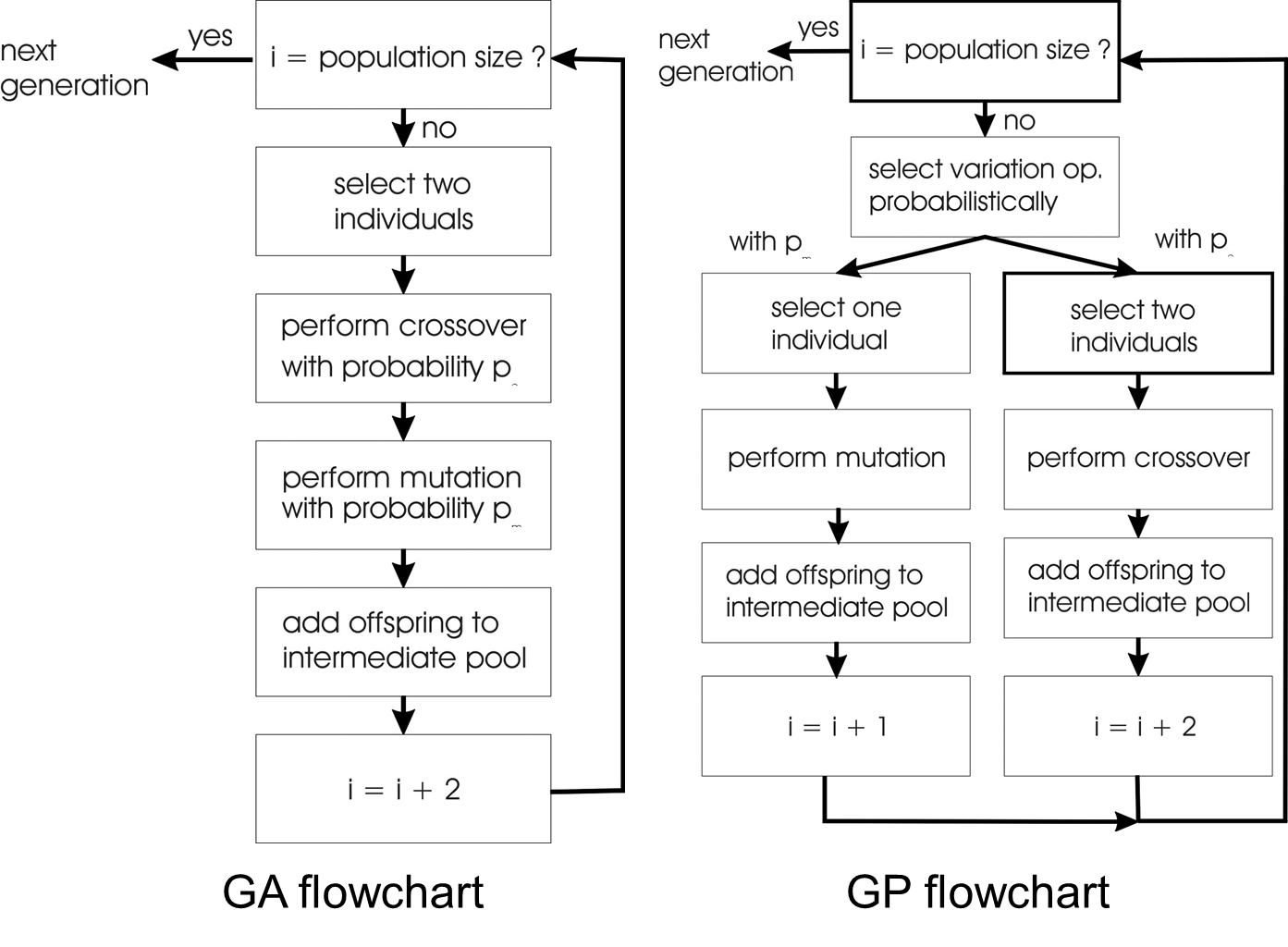
GA scheme using crossover AND mutation sequentially (be it probabilistically)
GP scheme using crossover OR mutation (chosen probabilistically)

1.5.8 GA vs GP

1.5.9 Selection

• Parent selection was typically fitness proportionate.
• Over-selection was used in very large populations.
  • rank population by fitness and divide it into two groups:
    • group 1: best x% of population,
    • group 2: other (100-x)%
  • Around f80% of selection operations chooses from group 1, 20% from group 2
  • for pop. size = 1000, 2000, 4000, 8000 x = 32%, 16%, 8%, 4%
  • motivation: to increase efficiency, %’s come from rule of thumb
• Survivor selection:
  • Typical: generational scheme (thus none)
  • Recently steady-state is becoming popular for its elitism

1.5.10 Initialization

• Maximum initial depth of trees D_max is set
• Full method (each branch has depth = D_max):
  • nodes at depth d < D_max randomly chosen from function set F
  • nodes at depth d = D_max randomly chosen from terminal set T
• Grow method (each branch has depth ≤ D_max):
  • nodes at depth d < D_max randomly chosen from F ∪ T
  • nodes at depth d = D_max randomly chosen from T
• Common GP initialisation:
  • ramped half-and-half, where grow & full method each deliver half of initial population

1.5.11 Bloat

Average tree sizes tend to grow during the course of a run.
This is known as bloat,
sometimes called the ‘survival of the fattest’.
This may be a broader phenomenon than GP.
Bloat is seemingly observed in organismal chromosomes as well.
Some small viruses show size constraints.
The simplest way to prevent bloat,
is to introduce a maximum tree size.
If the child(ren) resulting from a variation aperation would exceed this maximum size,
then the variation operator is forbidden from acting.
The threshold can be seen as an additional parameter of mutation and recombination in GP.
Another mechanism is parsimony pressure.
(i.e., being ‘stingy’ or ungenerous)
is achieved through introducing a penalty term in the fitness formula,
that reduces the fitness of large chromosomes,
or uses other multiobjective techniques.

1.5.12 Example symbolic regression

• Given some points in R², (x₁, y₁), … , (x_n, y_n)
• Find function f(x) s.t. ∀i = 1, …, n : f(x_i) = y_i
• Possible GP solution:
  • Representation by F = {+, -, /, sin, cos}, T = R ∪ {x}
  • Fitness is the error
    \(err(f) = \sum_{i=1}^n (f(x_i) - y_i)^2\)
  • All operators standard
  • pop.size = 1000, ramped half-half initialisation
  • Termination: n “hits” or 50000 fitness evaluations reached (where “hit” is if | f(x_i) - y_i | < 0.0001)

1.5.13 Modern sub-fields

Types of GP include:
Tree-based Genetic Programming
Stack-based Genetic Programming
Linear Genetic Programming (LGP)
Grammatical Evolution
Extended Compact Genetic Programming (ECGP)
Cartesian Genetic Programming (CGP)
Probabilistic Incremental Program Evolution (PIPE)
Strongly Typed Genetic Programming (STGP)
Genetic Improvement of Software for Multiple Objectives (GISMO)

1.5.14 Basic steps in generational, Tree-based GP:

1. Generate an initial, stochastic population.
2. Iteratively perform selection, genetic operation, and evaluation:
   • Evaluate each program (hypothesis) in the current population, against the given dataset and determine how well it performed, the value recorded as a fitness score.
   • Randomly select programs and compare their fitness scores.
   • Apply one of three genetic operators to a copy of the leading program:
     • reproduction
     • mutation
     • crossover
   • … then move the program into the subsequent generation.
   • Evaluate all programs (hypotheses) in each new generation.
3. Repeat until the user-defined termination criteria are met.

1.5.15 Modern software options

Review this briefly:
https://geneticprogramming.com/software/
Mention Clojush, Tiny Genetic Programming

1.5.16 Free books

http://www.gp-field-guide.org.uk/
06-PopularVariants/GP_book1.pdf

https://www.moshesipper.com/books/evolved-to-win/
06-PopularVariants/evolvedtowin.pdf
Mention his GP bot competitions.

And, our future lecture for this course:
18-GeneticProgramming.html

1.6 Learning Classifier Systems

https://en.wikipedia.org/wiki/Learning_classifier_system

Is much like an independent discovery of processes which resemble:
reinforcement learning, Q-learning, TD-learning.
https://en.wikipedia.org/wiki/Reinforcement_learning
https://en.wikipedia.org/wiki/Temporal_difference_learning
https://en.wikipedia.org/wiki/Q-learning (show images)

Read (show this briefly):
https://artint.info/2e/html/ArtInt2e.Ch12.html
https://artint.info/3e/html/ArtInt3e.Ch13.html

Animation on ch12 here (Java applets, lol):
https://artint.info/2e/online.html

Genome:
{condition:action:payoff}
{condition:action:payoff,accuracy}

Where payoff is like RL’s reward.

1.6.1 Quick overview Michigan-style

• Developed: First described in 1976
• Early names: Holland
• Typically applied to:
  • Machine learning tasks working with rule sets
  • Giving best response to current state environment
• Attributed features:
  • Combination classifier system and learning algorithm
  • Cooperation (iso usual competition)
  • Using genetic algorithms
  • Michigan-style (rule is individual) vs Pittsburgh-style (rule set is individual)

1.6.2 Technical summary table Michigan-style

1.6.3 Representation

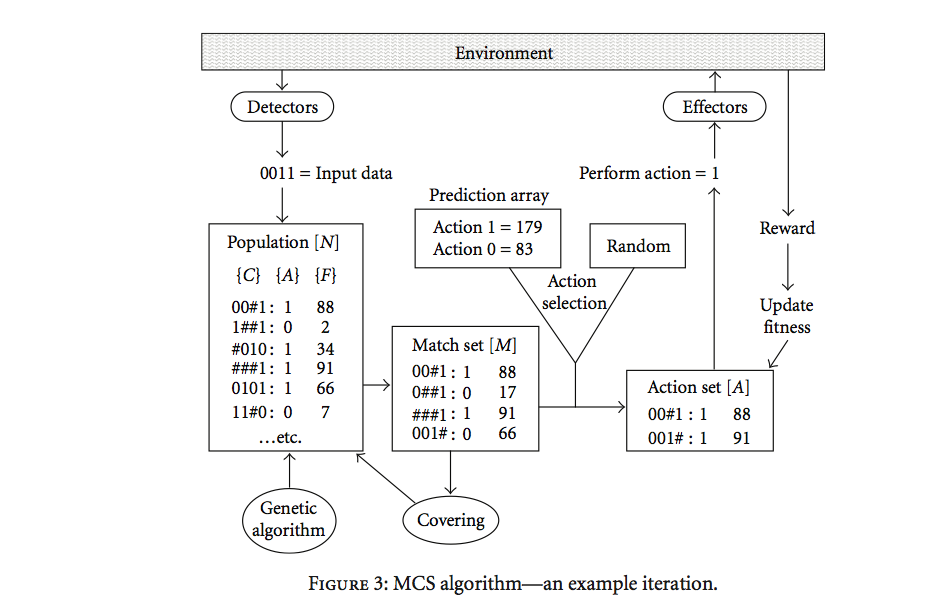
Each rule of the rule base is a tuple {condition:action:payoff}
Match set: subset of rules whose condition matches the current inputs from the environment
Action set: subset of the match set advocating the chosen action
Later, the rule-tuple included an accuracy value,
reflecting the system’s experience of how well the predicted payoff matches the reward received

1.6.4 Introduction example: the multiplexer

• k-bit multiplexer is bit-string with length k where
  • k = l + 2^l
  • l is the address part
  • 2^l is the data part
  • example: l=2, k=6, 101011 correct string
• Return the value of the data bit specified by the address part
• (take position 10 of data part 1011, which is 0)
• Rewards can be assigned to the correct answer

1.6.5 Iteration

1.6.6 Pittsburgh style

The Pittsburgh-style LCS predates,
but is similar to the better-known GP:

Each member of the evolutionary algorithm’s population represents a complete model,
of the mapping from input to output spaces.

Each gene in an individual typically represents a rule,
and a new input item may match more than one rule,
in which case typically the first match is taken.

This means that the representation should be viewed as an ordered list.
Two individuals which contain the same rules,
but in a different order on the genome,
are effectively different models.

Learning of appropriately complex models is typically facilitated by using a variable-length representation,
so that new rules can be added at any stage.
This approach has several conceptual advantages.
In particular, since fitness is awarded to complete rule sets,
models can be learned for complex multi-step problems.
The downside of this flexibility is that,
like GP, Pittsburgh-style LCS suffers from bloat,
and the search space becomes potentially infinite.
Nevertheless, given sufficient computational resources,
and effective methods of parsimony to counteract bloat,
Pittsburgh-style LCS has demonstrated state-of-the-art performance in several machine learning domains,
especially for applications such as bioinformatics and medicine,
where human-interpretability of the evolved models is vital,
and large data-sets are available,
so that the system can evolve off-line to minimize prediction error.
Two recent examples winning Humies Awards,
for better than human performance are in the realms of:
prostate cancer detection and protein structure prediction.

1.7 Differential Evolution

https://en.wikipedia.org/wiki/Differential_evolution

1.7.1 Quick overview

• Developed: USA in 1995
• Early names: Storn, Price
• Typically applied to:
  • Non-linear and non-differentiable continuous space functions
• Attributed features:
  • populations are lists
  • four parents are needed to create a new individual
  • different variants exist, due to changing the base vector
• Special:
  • differential mutation

1.7.2 Technical summary table

1.7.3 Differential mutation

In this section we describe a young member of the evolutionary algorithm family:
differential evolution (DE).
Its birth can be dated to 1995,
when Storn and Price published a technical report describing the main concepts behind a
“new heuristic approach for minimizing possibly nonlinear and non-differentiable continuous space functions”.
The distinguishing feature that delivered the name of this approach,
is a twist to the usual reproduction operators in EC:
the so-called differential mutation.

Given a population of candidate solution vectors in the set of real numbers, \({\rm I\!R}^n\),
a new mutant vector x’ is produced,
by adding a perturbation vector to an existing one,
x’ = x + p,
where the perturbation vector, p, is the scaled vector difference of:
two other, randomly chosen population members
p = F · (y − z),
where y and x are randomly chosen population members,
the scaling factor F > 0 is a real number,
that controls the rate at which the population evolves.

1.7.4 Uniform crossover

DE uses uniform crossover but with a slight twist
The other reproduction operator is the usual uniform crossover,
subject to one parameter,
the crossover probability Cr ∈ [0, 1]
that defines the chance that for any position in the parents currently undergoing crossover,
the allele of the first parent will be included in the child.

Remember that in GAs, the crossover rate pc ∈ [0, 1] is defined for any given pair of individuals,
and it is the likelihood of actually executing crossover.

In DE, at one randomly chosen position,
the child allele is taken from the first parent, without making a random decision.
This ensures that the child does not duplicate the second parent.
The number of inherited mutant alleles follows a binomial distribution

1.7.5 Evolutionary cycle

• Population is a list, not related to fitness value
• Creating a mutant vector population
  • For each new mutant, three vectors are chosen randomly from the population P (base vector υ and two others, y and z)
• Trial vector population is created
  • Uniform crossover between and
• Deterministic selection applied to each pair and
  • where the i-th individual in next generation is the one with highest fitness value

1.7.6 Different variants

• Different variants exists due to changing the base vector
• The variant is described as DE/a/b/c where
  • a is the base vector (rand or best)
  • b is the number of different vectors to define perturbation vectorexample four randomly chosen:
  • c denotes the crossover scheme (“bin” is uniform crossover)

1.8 Particle Swarm Optimization (PSO):

https://en.wikipedia.org/wiki/Particle_swarm_optimization
http://scholarpedia.org/article/Particle_swarm_optimization

1.8.1 Quick overview

• Developed: in the 1995
• Early names: Kennedy, Eberhart
• Typically applied to:
  • Optimizing nonlinear functions
• Attributed features:
  • No crossover
  • Every candidate solution carries it own perturbation vector
• Special:
  • inspired by social behavior of bird flocking/fish schooling
  • Particles with location and velocity iso individuals with genotype and mutation

1.8.2 Technical summary table

1.8.3 Representation

Every population member can be considered as a pair,
where the first vector is candidate solution,
and the second one a perturbation vector in \({\rm I\!R}^n\)

On a conceptual level every population member in a PSO can be considered as a pair <x, p>,
where \({x \in \rm I\!R}^n\) is a candidate solution vector and \({p \in \rm I\!R}^n\) is a perturbation vector,
that determines how the solution vector is changed to produce a new one.
The main idea is that a new pair <x’, p’> is produced from <x, p>
by first calculating a new perturbation vector p’
(using p and some additional information)
and adding this to x.
That is,
x’ = x + p’
The core of the PSO perspective is to consider a population member as a point in space,
with a position and a velocity,
and use the latter to determine a new position (and a new velocity).
Thus, looking under the hood of a PSO,
we find that a perturbation vector is a velocity vector v,
and a new velocity vector v’ is defined as:
the weighted sum of three components: v and two vector differences.
The first points from the current position x to the best position y the given population member ever had in the past,
and the second points from x to the best position z the whole population ever had.

The perturbation vector determines how the solution vector is changed to produce a new one.

• A member is considered as a point in space with a position and a velocity
• Perturbation vector is a velocity vector and a new velocity vector is defined as the weighted sum of three components:
  • Current velocity vector
  • Vector difference current position to best position of member so far
  • Vector difference from current position to best position of population so far
• where w and Φ i are the weights and U1 and U2 randomizer matrices
• Because the personal best and global best must be remembered, the populations are lists

1.9 Estimation of Distribution Algorithms

https://en.wikipedia.org/wiki/Estimation_of_distribution_algorithm
Estimation of distribution algorithms (EDA) are based on the idea of replacing the creation of offspring by ‘standard’ variation operators (recombination and mutation) by a three-step process.
First a ‘graphical model’ is chosen to represent the current state of the search,
in terms of the dependencies between variables (genes) describing a candidate solution.
Next the parameters of this model are estimated from the current population,
to create a conditional probability distribution over the variables.
Finally, offspring are created by sampling this distribution.

BEGIN
    INITIALISE population P 0 with µ random candidate solutions;
    set t = 0;
        REPEAT UNTIL ( TERMINATION CONDITION is satisfied ) DO
        EVALUATE each candidate in P t ;
        SELECT subpopulation Pst to be used in the modeling steps;
        MODEL SELECTION creates graph G by dependencies in Pst ;
        MODEL FITTING creates Bayesian Network BN with G and Pst ;
        MODEL SAMPLING produces a set Sample(BN ) of µ candidates;
        set t = t + 1;
        P t = Sample(BN );
    OD
END

1.10 Evolutionary Robotics

https://en.wikipedia.org/wiki/Evolutionary_robotics
http://scholarpedia.org/article/Evolutionary_Robotics

1.11 NeuroEvolution

https://en.wikipedia.org/wiki/Neuroevolution
http://www.scholarpedia.org/article/Neuroevolution
Discussed above!